麦卡勒姆规则
出自 MBA智库百科(https://wiki.mbalib.com/)
麦卡勒姆规则(McCallum Rule)
目录 |
麦卡勒姆规则简介[1]
麦克勒姆规则又被称为基础货币——名义GDP目标规则。与泰勒规则一样,它也是一个适应性政策方程,但具有不同的政策工具及其背后的不同的货币政策传导机制。麦克勒姆规则的政策工具是基础货币而不是联邦基金名义利率。根据这一规则,基础货币增长率依名义GDP增长率(或水平值)与设定的目标之间的离差而变动。这一规则中也包含了基础货币增长率的变化,在基础货币增长率变化不是很大时,名义GDP目标和基础货币目标可以说是等同的。
麦克勒姆规则包含三个主要部分:(1)名义GDP增长目标;(2)货币流通速度变化的移动平均值(即,相对于名义GDP的货币需求的变化);(3)名义与实际GDP之差。
- (一)麦卡勒姆一梅尔泽的基础货币规则
在以货币供应量为主要中介目标的20世纪80年代,基础货币是中央银行的一个重要操作工具。在这样的历史背景下,麦卡勒姆(1988)提出了一个基础货币规则,即中央银行遵循这个规则,根据宏观经济条件的变化对基础货币做出相应调整。几乎与此同时,梅尔泽(Meltzer)(1987)提出了相似的规则,因此也有人将此规则称为麦卡勒姆一梅尔泽规则。其表达式为:
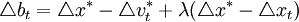
其中,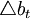 是基础货币对数值的变化,即基础货币在(t-1)到t期之间的增长率;
是基础货币对数值的变化,即基础货币在(t-1)到t期之间的增长率;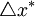 是名义GDP的目标增长率(麦卡勒姆赋值为4.5%),其目标值等于(
是名义GDP的目标增长率(麦卡勒姆赋值为4.5%),其目标值等于(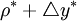 ),
),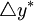 是实际GDP的长期平均增长率。该规则表达式右边的第二项
是实际GDP的长期平均增长率。该规则表达式右边的第二项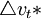 是前16个季度基础货币流通速度的平均增长率,vt = xt − bt为基础货币流通速度对数。这反映了由于技术进步或制度变化(假设为永久性变化)导致的对基础货币需求的长期持续变化,而不是为了反映经济景气情况。最后一项是误差校正项,该项表明当
是前16个季度基础货币流通速度的平均增长率,vt = xt − bt为基础货币流通速度对数。这反映了由于技术进步或制度变化(假设为永久性变化)导致的对基础货币需求的长期持续变化,而不是为了反映经济景气情况。最后一项是误差校正项,该项表明当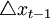 。低于
。低于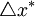 时,基础货币的增长速度就要调高以弥补目标的误差,麦卡勒姆选择其系数λ=0.5。
时,基础货币的增长速度就要调高以弥补目标的误差,麦卡勒姆选择其系数λ=0.5。
该规则的最终目标是稳定名义收入(名义GDP或名义GNP),因此,基础货币必须根据名义收入的实际增长率与目标增长率之间的差距进行阶段性调整。也有人将麦卡勒姆的这个规则称为名义收入目标规则。
麦卡勒姆用这个规则对美国1954~1985年的季度数据进行验证,他假设中央银行的目标通货膨胀率为0,根据美国历史上真实产出的长期增长率大概为3%,因此可以假设名义GDP的年增长目标为3%。通过比较名义GDP偏离其目标路径的均方差可以发现,使用麦卡勒姆规则可以使名义GDP非常紧密地靠近目标路径。
不可否认,不管是麦卡勒姆规则还是泰勒规则,他们的初衷都是为了降低通货膨胀率、减少经济波动。但实际上,在对英国20世纪80年代的货币政策的检验中,这两个规则却给出了完全不同的结论:麦卡勒姆规则认为应该紧缩政策,而泰勒规则认为应该放松,实际上面对当时快速上升的高通货膨胀,紧缩政策可能更合理。因此尽管泰勒规则更受青睐,而且目前大部分国家都采用利率作为货币政策工具,但在政策决策时也不能仅机械地遵循一种规则。
- (二)麦卡勒姆一纳尔逊利率规则
尽管与泰勒规则相比,麦卡勒姆基础货币规则中的所有变量都更容易测量,但基础货币本身的测量却有点麻烦,像在美国,由于很不稳定,这个变量只在很短时间的样本中用过(1979~1982年)。因此,麦卡勒姆和纳尔逊(1999)从基础货币规则转向了利率规则(联邦基金利率),其表达形式就像上式中的误差校正项:
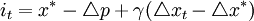
其中,it为名义利率,p是一般价格水平的对数,参数γ比λ大(麦卡勒姆取γ值为1.5)。之所以将货币政策工具由基础货币转向利率,除了数据的可得性原因之外,还因为他们相信基础货币流通速度和联邦基金利率之间具有稳定的关系,即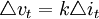 ,而
,而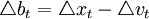 ,根据基础货币规则,有:
,根据基础货币规则,有:
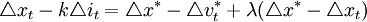
整理后得到:
![\triangle i_t=[\triangle v_t^*+(1+\lambda)(\triangle x_t-\triangle x^*)]/k](/w/images/math/0/4/8/048c6ffc5d01f561e7d988daa55d8ca9.png)
即得到联邦基金利率变化的规则。
麦卡勒姆规则的产生背景[2]
从1970年代初开始,美国货币当局采用弗里德曼的政策主张,以保持稳定的货币增长率。从实际效果看,在此后近十年的时间内,货币增长率相对稳定,但产出和通货膨胀却出现了剧烈波动。于是,人们便怀疑货币供应量目标的有效性。面对这些问题,麦卡勒姆认为弗里德曼规则是在假定货币需求和货币流通速度不变的前提下保持货币供应量以固定的比例增长,显然,这些前提并不能得到满足。因此,基础货币应根据货币流通速度和目标变量的变化进行阶段性调整,才能使该规则具有更强的适应性。
麦卡勒姆规则是在弗里德曼规则(Friedman,1982)的基础上发展起来的,它对后者作了三个重要修正。一是以基础货币(而不是弗里德曼主张的货币供应量)为工具。因为货币供应量既不是货币政策的最终目标,也不是中央银行可直接控制的政策工具,因此,在发生重大制度变迁时,中央银行不能使其达到预定目标,而基础货币则不然,在一定条件和相关的财政政策配合下,调控基础货币可能达到预定目标。二是考虑了基础货币流通速度的变化。
基础货币应当根据流通速度的变化进行阶段性调整,即两者呈反方向变化。如果基础货币以不变的比率增长,则不但达不到合意的目标,反而会加剧货币供应量和实际经济的波动。三是把稳定名义收入作为货币政策的最终目标。因而,基础货币必须根据名义收入的实际增长率与目标增长率之间的差距进行阶段性调整。心。由于名义收入与价格水平和真实产出之间存在恒定的关系,所以,以名义收入为目标的优点之一便是可间接地控制通货膨胀。
麦卡勒姆规则被提出后,一些经济学家利用货币政策的实践对其进行了实证检验,以考察使用麦卡勒姆规则(或它的扩展形式)在稳定通货膨胀和实际产出方面的影响。麦卡勒姆本人(MeCallum,1987)利用美国1954—1985年的历史数据,对麦卡勒姆规则的原式进行了回归分析,结果显示,使用该规则可使名义国民生产总值(GNP)非常紧密地靠近目标路径。同时,模型还考察了名义收入缺口的反应系数入取不同值时的情况,相比较而言,原式的效果更好。Croushore和Stark(1995)选择了三种宏观经济模型(凯恩斯主义模型、PSTAR+模型和理性预期模型)来模拟运用麦卡勒姆规则时经济的运转情况。从模拟的结果看,如果按麦卡勒姆规则进行操作,平均真实产出可接近其潜在水平,同时,模拟的价格大大低于历史水平。然而,只有在PSTAR+模型中,实际GNP和价格水平两者才都是稳定的。
Judd和Motley(1991)则考察了在凯恩斯模型、真实商业循环模型和向量自回归模型三种模型下麦卡勒姆规则及其扩展形式(主要是修正后的名义GNP规则和价格水平规则)的表现。在大多数情况下,使用规则时通货膨胀的波动要比没有规则时小,唯一例外的是修正后的名义GNP规则在真实商业循环模型假设下通货膨胀的波动比没有规则时更宽。在三种规则的对比中,名义GNP规则在各种不同的模型中比其他规则具有更强的稳定性。为了检验麦卡勒姆规则是否会带来更大的产出波动,他们还考察了名义GNP规则在1989年的两季度中实际GNP增长率的表现。在实际商业循环模型中,所有规则对实际GNP的增长都没有影响;而在其他模型中,使用规则的波动在多数时候要比不使用规则时更大一些。这说明,使用规则可能会增加实际GNP的短期波动性。此后,Judd和Motley(1993)又对以利率工具为变量的麦卡勒姆规则进行了检验。从结果来看,使用以基础货币为工具、名义国内生产总值(GDP)为目标的规则所导致的平均通货膨胀率最低,远低于实际值5.4%,而且最为稳定。而以利率为工具的规则在大多数情况下可能有很高的置信度来保证使通货膨胀率在接近于零的小范围内波动,但是在仅有比例项的情况下可能导致发散性的情况。
如果从实证分析方面考虑,与其他规则相比,麦卡勒姆规则更加适合于中国的现实。这是因为:第一,麦卡勒姆规则以基础货币为控制工具,这和中国中央银行的政策工具是相同的。第二,麦卡勒姆规则无需分别估计通货膨胀缺口和真实产出缺口,而只需估计名义GDP缺口。这与中国每年只公布名义GDP目标(即产出目标)而没有相应的通货膨胀目标和实际产出目标的情况相吻合。正是从这种角度出发,选择麦卡勒姆规则对中国的货币政策操作进行实际检验。但在实际运用过程中,需要根据中国的实际情况对一些变量和参数进行相应的调整。首先,对于麦卡勒姆规则反应函数的具体形式,包括工具和目标变量的选择以及参数的取值,都没有统一的看法。由于真实GDP的潜在增长率的可预测性较弱,在模型中剔除了这一变量,仅考虑名义GDP及其增长率。同时,根据已有数据估计反应函数的参数值,并计算出规则模拟的基础货币及其增长率,以便于比较其与实际值的偏差。其次,麦卡勒姆规则原本是建立在浮动汇率制的基础上,但中国实行的是盯住美元的汇率制度。为维持汇率稳定,中央银行必须在市场进行外汇买卖操作,而这一过程又会导致基础货币投放量的变化。因此,在建立反应函数时,需考虑固定汇率制度的影响。
麦卡勒姆规则的扩展[3]
麦卡勒姆规则产生以后。许多经济学家从许多方面扩展了该规则(具体来说。主要包括以下两个方面:
- 1.对规则目标的扩展
麦卡勒姆重新构造了以通货膨胀为目标的基础货币规则。规则的形式为,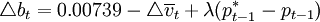 (1)
(1)
其中,pt − 1表示前一期的通货膨胀,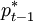 表示中央银行的通货膨胀目标。
表示中央银行的通货膨胀目标。
贾德和莫特利则将名义收入目标分解为真实收入目标(y)和通货膨胀目标(p)。具体的规则形式如下:
![\triangle b_t=(\triangle y^f_t+\triangle p_t^*)-\triangle\overline{v}_{t-1}+\lambda[(y^f_{t-1}-y_{t-1})+(\triangle p_{t-1}^*-\triangle p_{t-1})]](/w/images/math/e/a/c/eac6ed60e56c5417dc386f95198a4056.png) (2)
(2)
为了考察上述规则和稳健性。他们使用了菲利浦斯曲线模型、真实经济周期模型和向量自回归模型等宏观经济结构模型。比较这些规则在不同的模型假设之下的表现。结果发现。与没有规则时相比。使用上述规则可以使平均通货膨胀率为零。而且还可以使通货膨胀的波动比没有规则时小得多(但是总体来看。规则(1)和(2)的稳健性不如规则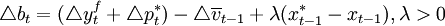 。因为当反应系数;的取值超过一定的范围。规则(1)和(2)在一些模型假设下可能会导致发散性的结果。
。因为当反应系数;的取值超过一定的范围。规则(1)和(2)在一些模型假设下可能会导致发散性的结果。
杜克尔和费希尔考察了货币当局具有多重目标时的情形(在他们的模型中。中央银行以稳定价格和汇率为目标。并且允许参数随时间的变化而变化。而霍尔等人在一篇文章中曾经使用预期的名义收入为目标。考察英国的货币政策(模型的形式为:

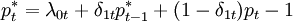
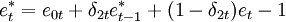 (3)
(3)
其中p、e为分别是以对数来衡量的价格水平和汇率;p * ,e * 是它们的目标值;λmt,m = 0,1,2是服从马尔科夫转换过程的参数;ε为随机扰动。且ε-N(0,σε)。
不过根据麦卡勒姆的研究。这种前瞻性的名义收入规则有很强的模型依赖性。因此。在稳健性方面要大大低于简单的麦卡勒姆规则。
- 2.对规则工具的扩展
麦卡勒姆考察了使用短期利率(90天的国库券收益率)为工具的名义收入规则(不过。他认为名义利率与通货膨胀之间的动态关系是使用该规则的一大难点。因为一般看来。高利率可以降低需求。从而减轻通货膨胀压力。但是。从较长时期来看。高利率又是加速通货膨胀的结果。
因此。这就出现了一个相互矛盾的结论,为了实现低利率。中央银行需要就必须提高利率以便降低通货膨胀。尽管如此。麦卡勒姆还是考察了如下利率规则:
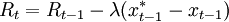 (3)
(3)
其中R表示短期利率,系数λ为正。
但是。麦卡勒姆对上述利率规则的模拟结果却不尽如人意λ的最优取值在0.03左右。而且会比麦卡勒姆的原式导致更大的均方根差。如果λ的取值充分低于0.03。则该利率规则无法提供足够的反馈。因而不能保持名义收入接近其目标路径;如果;的取值超过0.03(如;λ=0.05),就会出现发散性摆动(因此。麦卡勒姆将滞后两期的名义收入引入利率规则。希望考察利率的稳定性。规则的形式为:。
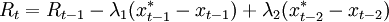 。
。
假设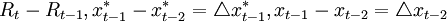 那么上式可化为:
那么上式可化为:
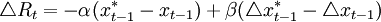 (4)
(4)
其中,α = λ1 − λ2,β = λ2其中右边第一项表示名义收入缺口的比例项,第二项表示名义收入缺口的导数项。即名义收入增长率的变动;模拟的结果表明,当λ1 = 1.0,λ20.9时,上述规则明显可以以极高的概率收敛到名义收入的目标值。不过这个结果具有欺骗性:虽然名义收入的总量达到了目标值,但检查价格水平和产出的增长路径可以发现,真实产出的增长率几乎为零,而价格水平具有一个大于零的值,因此,上述规则并没有达到稳定价格的目标。
McCaIlum规则在西方发达国家的应用比较[4]
McCallum认为,美国在20世纪的整个70年代,实际利率值低于按照其规则计算的理论利率值,说明这一时期美国的货币政策比较宽松。这与当时美国正面临着严重的通货膨胀,需要采取紧缩的货币政策是相吻合的,McCallum规则符合这一时期的实际情况。进入80年代之后,直到1987年,按照McCallum规则计算的结论,货币政策又过于紧缩。1987年~1996年,按照规则货币政策比较合适;但1996年之后货币政策又有些紧缩。
在英国,McCallum规则说明,整个20世纪70年代的货币政策太松了。因为按照规则,要求1973年的利率为38%,而实际的利率值仅为10.4%。1983年~1987年,货币政策又稍紧。自1987年之后,除1994年,货币政策都是比较适宜的。
日本的情况也一样,McCallum规则说明,1973年~1978年应该稍紧一些,1982年~1987年间的大部分时间,货币政策却又过于紧缩。而1994年之后的大部分时间,除1997年,货币政策又开始紧缩。如规则要求1998年的利率是_3.6%,而实际的利率却是4%。
麦卡勒姆规则与泰勒规则比较[5]
麦卡勒姆规则与泰勒规则比较麦卡勒姆规则与泰勒规则的区别在于,操作工具和目标变量的不同。两种规则中,究竟要选择哪一种?这依赖于具体的经济情况。
按照正统的观点,1995-1998年日本货币政策难以刺激经济,因为利率已经很低。而按照麦卡勒姆规则,基础货币仍处于紧缩过程,表明期间货币政策过于紧缩(McCailum,1999,p.9)。
对于美国的货币政策,按照泰勒规则,70年代实际利率已经低于规则所拟合的水平;而麦卡勒姆规则表明,70年代货币政策过于放松,实际基础货币增长高于麦卡勒姆规则所拟合的水平,而且这种差异在1981-1987年有所缩小。这里,名义GDP增长作为目标变量要比利率规则更有效。
利用泰勒规则对于英国70年代过于放松的货币政策进行评价,结果表明,建议的政策利率为38%,而当时的实际利率为10.4%。1983-1987年货币政策过于紧缩,1987年以来的政策取向是对的。然而,麦卡勒姆规则的解释则有所不同,70年代的政策过于放松,而且直到1990年大多时候仍过于放松。
对于日本经济来说,泰勒规则表明,1972-1974年货币政策应该紧缩,而在1982-1987年大多数时候货币政策过于紧缩。麦卡勒姆规则表明,90年代中期货币政策过于紧缩。
麦卡勒姆(McCallum,2000)用历史分析方法对60年代初到1998年,美国、英国和日本(日本为70年代初)的货币政策决策进行了分析,并使用泰勒规则和麦卡勒姆规则相结合进行分析。对于泰勒规则有许多扩展的形式,包括利用预期未来通货膨胀代替公式中的实际通货膨胀。最常见的是,在泰勒规则的右边加上实际短期利率的滞后变化it − 1,如此得到泰勒规则的变式。
有关货币规则的研究表明,各种规则与工具变量有密切关系,反映了规则具有以下基本性能:第一,所采用的规则实际上作为指标变量,而非工具变量。即是说,可以将利率和基础货币变化作为中介目标,而把其他变量作为中央银行工具的变量进行逐日操作;第二,政策的状态或松或紧,可由利率或基础货币变化的设定表示,并参照其他变量。
为了解决时间不一致问题,货币当局需要事先采取规则。这样,有利于形成公众预期,一旦规则公开,货币当局应该努力达到,否则,货币政策的可靠性就会降低。为此,有人建议中央银行要直接控制基础货币或狭义货币,稳定某些可观察和度量的变量的增长。
中央银行要控制哪一种工具?麦卡勒姆规则提出,使用基础货巾作为隐含工具,名义GDP对现有途径的偏差可以作为反馈。
托马斯(1homas,1997,p.325)提出,基础货币是中央银行资产负债表中的净货币负债。从基础货币的运用来看,包括流通中的货币、存款机构在中央银行的存款;从基础货币的来源来看,具有正的影响包括资产组合、贴现和透支、货币发行、黄金储备和SDR账户(特别提款权账户)、持有财政发行货币;具有负的影响的方面包括财政在中央银行的存款、外国和其他机构在中央银行的存款、财政持有的钞票以及其他负债和资本。
古德哈特(goodhart,1994)批评把基础货币作为货币政策内含工具,基础货币的可行性和合意性是一个处于争论的问题。不过,在麦卡勒姆规则中,通过利率调整使基础货币增长与所要求的货币政策最终目标相配合是有效的。基础货币作为一种信息变量有其吸引力。从概念上看,中央银行资产在经济平衡水平中处于重要地位。从实践来看,在英国,二次世界大战以后,基础货币流通速度趋势比较平稳,而且具有可测性。
![\triangle b_1=\alpha-(\frac{1}{16})[x_{t-1}-b_{t-1}-x_{t-17}+b_{t-17}]+\lambda[x^*-x]_{t-1}](/w/images/math/9/f/c/9fcbf34239aa6cd919e09c42d83f8bf2.png) (1)
(1)
霍尔丹、麦卡勒姆和萨门(Haldane,McCallum,andSa]Inon,1996)根据麦卡勒姆规则的如下形式,对英国基础货币的有关规则进行研究:其中,b为基础货币的对数,x为名义GDP的对数,*为目标值。所有数据为季度值。
常数项α为静态下的名义收入增长,英国的这一值为1%,与名义GDP年增长4%相对应。公式(1)中的第二项为现行的基础货币流通趋势,其为前4年移动平均值。目的是要考虑较长时期内机构变化的内含。第三项为政策反馈参数,表明GDP偏离其目标值而通过货币政策作出反应的速度(取值为0到1)。
对于英国基础货币规则的研究表明,这一规则能够保证通货膨胀不高于2%,而且使货币政策工具或实际产出易变性更小。这一规则可作为英国现行货币政策框架的有益补充,防止货币政策出现较大失误。
克拉克、古德哈特和黄(Clark,Goodhart,and Huang,1999,p.513)提出,在承诺规则和随意规则的情况下探求最优货币政策时,价格和通货膨胀的持续性是所有菲利普斯曲线实际模型的共同特征。短期内,产出与通货膨胀之间存在替代性,但就长期来看,经济本身具有自动恢复稳定的机制。尽管通货膨胀最终依赖于货币存量增长率,产出的短期稳定和通货膨胀则依赖于实际利率的调整,因为利率可以影响到总需求和产出能力的变化,进而影响到通货膨胀。
由于通货膨胀的持续性,承诺规则和随意规则策略都会导致静态依存和震动反馈规则,产出的持续性对最优货币政策规则具有重要影响。此外,事前预期总是存在于两种最优货币政策规则的替代关系中。考虑承诺规则的政策行动对市场预期的影响,其中只考虑到利率调整对经济的影响,而没有考虑到市场对货币当局操作规则的反应。承诺规则使预期通货膨胀接近于通货膨胀目标,同时,预期产出则远离其目标水平。对于随意规则,则相反。随意规则对于减少随机震动对通货膨胀的影响更为有效,因而,随意规则条件下,随机震动对产出的影响要比承诺规则更大。
许多人从历史分析和计量统计得出,货币政策对实际产出具有较大影响,实证分析表明货币具有非中性的特点。鲍尔和克劳肖(Ball,and Cmushore,1998)对联邦基金利率作为货币政策变化的度量,以专家预测作为预期,结果表明,联邦基金利率的上升对实际产出要比对预期产出的影响更大,表明经济主体低估了政策对总需求产生的效应,这样,货币政策的真实效应表现为,对理性预期具有负效应。此外,实际利率的上升会导致随后2年通货膨胀的下降,以及几乎相等的预期通货膨胀-下降。
对于货币政策的实际影响,鲍尔和克劳肖(Ball,and Croushore,1998,p.8)通过实证分析说明,货币政策对于实体经济的影响具有一定时滞,一般来说,货币政策紧缩会产生随后2-3年的通货膨胀下降,以及随后1年的产出效应。
赫斯、斯莫尔和布雷顿(Hess,Small,and Bmyton,1993)提出,麦卡勒姆为了寻求美联储能够直接控制的政策工具,选择了基础货币作为政策工具。由于经济学家尚未对宏观经济模型达成共识,需要对不同模型条件下麦卡勒姆规则进行估计,并使样本更新到1992年。
考虑基础货币作用的以下两种形式:一是,基础货币直接与支出相联系;二是,货币传导机制通过利率运作。由此,得出以下结论:基础货币与名义产出之间的关系看上去有所减弱,主要在于增长的流通速度有较大变化。通过利率进行货币政策传导时,麦卡勒姆的基础货币工具的预测能力与利率对基础货币的敏感度有关,同时短期利率变化通过长期利率进行传导。这种情况下,对名义收入的可控性较好。最后,有关模型结果表明,使用联邦基金利率作为政策性工具具有积极的效果。
然而,从历史上看,基础货币的增长本身不具有稳定性,由于统计原因,以美国的基础货币增长为例进行分析。从1920年1月到1996年4月,以10年为时间单位。每一个10年中,每个月底的12个月基础货币增长从5%到35%不等。10年平均来说,也从0.8%到10%不等(见下表)。
表美国基础货币增长(1920-1996)
| 时期 | 12个月基础货币增长最大值(%) | 12个月基础货币增长最小值(%) | 10年内平均(%) |
| 20年代 | 11.3 | -15.5 | 0.8 |
| 30年代 | 26.6 | -5.7 | 10.0 |
| 40年代 | 25.7 | -9.4 | 10.4 |
| 50年代 | 9.8- | 8.5 | 1.1 |
| 60年代 | 6.9 | 0.4 | 4.2 |
| 70年代 | 9.7 | 5.5 | 7.9 |
| 80年代 | 10.4 | 3.8 | 7.4 |
| 90年代 | 11.4 | 2.1 | 8.0 |
注:有关数据为该年代任何一个时期为12个月基础货币增长的最大值或最小值。
杜克和费歇尔(Dueker,and Fischer,1998)对麦卡勒姆规则进行了考察,结果表明,名义收入反馈规则(nominal feedbaek rules)可以作为货币政策的参考指标。







