頻數分佈表

出自 MBA智库百科(https://wiki.mbalib.com/)

頻數分佈表(Frequency Distribution Table)

　　將一組計量資料按觀察值大小分為不同組段，然後將各觀察值歸納到各組段中，最後清點各組段的觀察值個數(稱頻數)，以表格形式表示之，稱為頻數分佈表又稱“頻次分佈表”，簡稱“頻數表”。

　　1、描述資料的分佈特征和分佈類型。

　　頻數分佈有兩個重要特征：集中趨勢和離散趨勢。大部分觀察值向某一數值集中的趨勢稱為集中趨勢，常用平均數指標來表示，各觀察值之間大小參差不齊。頻數由中央位置向兩側逐漸減少，稱離散趨勢，是個體差異所致，可用一系列的變異指標來反映。

　　2、便於進一步計算有關指標或進行統計分析。當數據較多且需手工計算時，常先編製頻數表，再進行統計計算。

　　3、發現特大、特小的可疑值。

　　如果頻數表的一端或兩端出現連續幾個組段的頻數為零後，又出現少數幾個特大值或特小值，使人懷疑其是否準確，需進一步檢查和核對並做相應處理。

　　4、據此繪製頻數分佈圖。

　　製作頻數分佈表的兩個基本原則：

　　第一，用來製作頻數分佈表的原始數據都能出現在該表中；第二，任一個原始數據只能出現在該表的一個組中，不能同時兼屬兩個組中。

　　根據第二原則，製作頻數分佈表時，組與組之間應該有明確的界限，即組限，每組的起點稱為組下限，而每組的止點稱為組上限。由此可見，對計量資料而言，組限應是閉一開區間，而對計數資料而言，組限應是閉區間。根據第一原則，如果組限是由小到大的順序排列的，則第一組的下限應小於等於原始數據資料的最小值，最後一組的上限應大於等於原始數據資料的最大值。反之則相反。

　　頻數分佈表的編製方法：

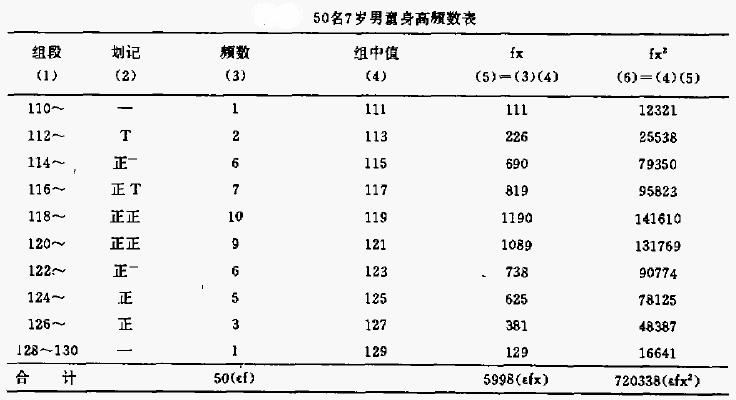
　　例：某市1982年50名7歲男童的身高(cm)資料如下，試編製頻數表。

114.4　　117.2　　122.7　　124.0　　114.0　　110.8　　118.2　　116.7　　118.9　　118.1

123.5　　118.3　　120.3　　116.2　　114.7　　119.7　　114.8　　119.6　　113.2　　120.0

119.8　　116.8　　119.8　　122.5　　119.7　　120.7　　114.3　　122.0　　117.0　　122.5

119.7　　124.9　　126.1　　120.0　　124.6　　120.0　　121.5　　114.3　　124.1　　117.2

120.2　　120.8　　126.6　　121.5　　126.1　　117.7　　124.1　　128.3　　121.8　　118.7

　　1、找出觀察值中的最大值（largest value）、最小值（smallest value），求極差（range）。

　　極差等於最大值減最小值。本例最大值=128.3，最小值=110.8，則極差=128.3-110.8=17.5(cm )

　　2、確定分組數和組距（class interval）。

　　組數的多少是根據例數的多少來確定的，以能夠反映出頻數分佈的特征為原則，一般分10—15組。組距為相鄰兩組的間隔，組距=極差/組數。本例擬分10組，則組距=17.5/10=1.75≈2，為劃記方便，可取稍大或稍小的數(當然本例組距也可取1.5)。

　　3、確定組段。

　　第一組段包括要最小值，取較最小值稍小且劃分方便的數，本例取“110～”。最後組段包括最大值並寫出其上限值。

　　4、劃記。

　　將各觀察值以劃“正”字的方法，一筆代表一例，劃在相應組段中。例如第一個數l14.4應在組段“114～”處劃，第二個數117.2應在“116～”處劃，以此類推。

　　5、統計各組段的頻數。全部數據劃記完後，清點各組段的人數。

根據編製出的頻數表即可瞭解該數值變數資料的頻數分佈特征。