EDF模型
出自 MBA智库百科(https://wiki.mbalib.com/)
EDF模型(Expected Default Frequency)
目錄 |
EDF模型即“預期違約率模型”,是著名的風險管理公司KMV公司開發的用以衡量違約風險基本工具。該模型最主要的分析工具是所謂的預期違約率EDF(Expected Default Frequency),故也稱為EDF模型。EDF作為度量公司違約發生可能性大小的指標,根據實證數據顯示,其早期偵測(early detecting)違約風險能力成效卓著;再者,應用選擇權觀念所建立之違約風險衡量指標,於信用分析領域中,獨樹一格。
對於一個公司而言,違約風險是指圍繞其償債能力所產生的不確定性。在違約之前,我們無法明確判斷一個公司是否會違約,充其量也只能對其違約的可能性做出概率上的估計。一家公司的EDF是指該公司在未來一年或幾年內違約的概率,它主要由三大因素決定,分別是:
1.資產價值:公司資產的市值。它是公司資產在未來產生的現金流以一定的貼現率貼現到當前的價值。這個公司資產的測度不但反映了公司的發展前景,而且還包含了公司所處的行業以及巨集觀經濟狀況等信息。
2.資產風險:是指資產價值的不確定性。這是一個關於公司經營風險和行業風險的測度。因此公司的資產價值只是一個估計值,存在一定不確定性,應當在公司的經營風險或者資產風險的框架下理解。
3.債務水平:是指公司在合同上負債的程度。如果說與公司資產相關的測度是公司的市值,那麼公司杠杠比率的相關測度就是相對於公司資產市值的債務面值,因為它是公司必須償還的金額。
當公司的資產價值低於一定水平時,公司就會對債權人和股東違約,與這一水平相對應的資產價值為違約點(Default Point),即公司資產價值等於負債價值時的點。在研究違約的文獻中,我們已經發現當公司資產價值等於債務面值時許多公司並沒有選擇違約,而是依然經營並償還它的債務,這是因為債務構成中的部分長期債務為公司提供了一定的緩息空間。我們發現,違約點即公司將會發生違約時的資產價值通常是介於總債務和短期債務之間。
因而公司凈值也就等於公司的資產市值減去公司的違約點,即:
公司凈值=公司的資產市值-違約點
當公司凈值等於零時,違約事件就會發生。和公司的資產價值一樣,公司凈值的測度也必須在公司經營風險的框架下考慮。比方說,食品和飲料行業內的公司比高科技行業能承受更高水平的杠桿比率,因而它們的資產市值更加穩定、有著更小的不確定性。
公司的資產風險則是由資產的波動率來衡量的,它是指公司資產價值每年變動百分比的標準差倍數,它是一個與公司的規模以及所處的行業都相關的測度。
資產的波動率與股票的波動率相關,卻又不同於它。一個公司的財務杠桿具有放大其資產波動率的作用。因此,有著較低資產波動率的行業,如銀行業趨向於採用較高的財務杠桿,而資產波動率較高的行業,如電腦軟體行業,則趨向於採用較低的財務杠桿。正是由於這種趨向差異的存在,股票波動率不像資產波動率那樣隨行業和資產規模的不同有較大的差別。
資產價值、經營風險、財務杠桿能夠結合起來形成一個違約風險的單一測度,它將公司的凈值與資產價值一個標準差的波動幅度相比較,將二者的商稱為違約距離(DD,Distance to default),其計算過程如下:
違約距離(DD)= (資產市值-違約點)/(資產市值*資產波動率)
從上式可以看出,違約距離融合了一個公司三個關鍵的信用要素:資產價值、經營和行業風險以及財務杠桿。KMV公司選定一定時期,基於一個包括大量的公司違約信息的歷史資料庫,把違約距離與預期違約率的關係擬合成一條光滑曲線,從而找出違約距離與預期違約率之間的映射關係以便估計EDF的值。也就是說,給定一個違約距離就可以計算出相應水平的預期違約概率。
對一個公開上市的公司而言,市場上與其違約概率相關的基本信息有三種,分別是財務報告、公司債券和股票的市價、市場上對公司前景和風險的主觀評價。價格從本質上講都有前瞻的內在特性,投資者對公司未來的預期形成了債券和股票的價格。在決定市場價格的時候,投資者使用了各種各樣的信息,這些信息包括:公司前景和風險的主觀評價、財務報告以及市場上的其它價格。投資者們通過自己的分析和判斷將這些信息融合為自己買賣公司股票、債券的意願,而市場價格正是許多投資者買賣意願的綜合結果,因而市場價格包含了許多投資者的綜合觀點和預測。用市場價格能為估計增加很強的預測力,使模型更具有前瞻性。KMV公司確定一個公司EDF的全過程,主要有三個步驟:(1)估計資產價值和資產波動率;(2)計算違約距離;(3)計算EDF。
如果股票市價是可得的,那麼資產的市值和波動率將可以通過期權定價方法直接得到。這種方法將股票視為公司資產的一項買入期權。股票的特點使得持股者擁有公司在償還債務之後接手公司剩餘資產的權利,而非義務。因而,可以將股票看作是公司資產的一項買入期權,而這項期權的執行價就等於公司債務的面值。
在BSM模型框架下,公司債務只包括單一級別的股票和單一級別的債券,並假定公司資產的市場價值服從以下隨機過程:
由上可知,在公司資產市值和資產波動率知道之後,對違約概率的計算的關鍵就是違約點的確定。KMV公司根據對違約的實證分析發現違約發生最頻繁的分界點在公司市場價值大約等於流動負債加減50%的長期負債時,因此KMV公司選擇的違約點等於短期債務(一年及以下)的價值加上未償長期債務賬麵價值的一半,這樣違約距離就可以通過下式計算出來:
違約距離= (資產市值-違約點)/(資產市值*資產波動率)
如果違約距離的分佈已知,那麼違約概率就可以簡單的看作是資產價值低於違約點的概率。然而,在實踐中,違約距離的分佈是很難度量的,而且,通常對違約距離做出的正態分佈或對數正態分佈假定也是不合理的。在對違約進行度量的過程中,公司資產價值和違約點之間關係發生逆向改變的可能對精確確定違約概率是十分關鍵的,這些改變可能是由於公司資產價值或是債務水平的變化所導致的。因此,KMV公司首次將違約距離定義為公司資產價值偏離違約點的標準差倍數,然後應用歷史數據來決定相應的違約概率。
違約發生在公司資產價值低於公司債務面值,則可將違約概率表示成:
EDF具有一些明顯的優點的同時也存在一些缺陷。
EDF的優點在於EDF是基於市場價格計算出來的,因此它有很好的前瞻性,能及時、可靠的反映上市公司信用狀況。EDF指標來自於股票價格的實時行情數據的分析,而不是以歷史的會計數據為基礎,股票價格不僅反映了公司的歷史和現狀,還具有對公司未來的前景預測。由於模型是以股票市場數據為基礎的,這為投資者、債權人、監管機構等相關人員和部門提供可靠的信用風險評價信息。
EDF應用過程中的缺陷在於, EDF反映的是預期的違約概率,而非實際的違約概率,它是一個通過歷史數據模擬出來的指標,是對實際違約概率的一個估計值。而且EDF的計算需要有強大的公司違約信息資料庫為支撐,數據不足則計算準確度不高。
案例一:基於EDF模型的上市公司信用風險分析[1]
選擇上市公司作為研究樣本。對於方程式E = VN(d1) | − De − πN(d2) (1)與 企業的資產杠桿比率 (2)
企業的資產杠桿比率 (2)
首先需要計算企業股權市場價值及其波動率。JohnC.Hull對股票價格波動率的研究表明使用近90天到180天的每日股票收盤價估計其波動率的效果相當不錯。在以下研究中,將選180天作為時間基數。由於方程式(1)與(2)較為複雜,利用VC++編程來對方程進行求解,並對方程式(1)與(2)分別作以下變換:。
f(V) = VN(d1) − De − πN(d2) − E (3)
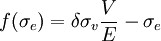 (4)
(4)
程式的基本演算法如下:(1)首先資產市值波動率的初值用股權市值波動率來代替,代入方程(3),求出相應的資產市值;(2)以(3)中計算的資產市值代入方程(4),求出相應的股權市值波動率;(3)如果(4)中計算出來的股權市值波動率等於真實的股權市值波動率,則程式終止。否則調整資產市值波動率,重覆以上步驟,直至算出相應的結果。
對於方程式(3)與(4),我們需證明方程的解為唯一解。我們對方程式(3)求導整理得:
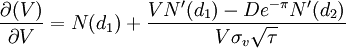 (5)
(5)
因為: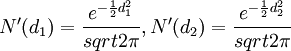
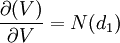 (6)
(6)
因為N(d1) > 0,所以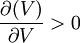 ,f(V)是關於V的遞增函數,因而f(V)有唯一解。
,f(V)是關於V的遞增函數,因而f(V)有唯一解。
顯而易見,對於方程式(4)當其他參數確定時,σe為唯一解。
選擇了30家上市公司為樣本對其1998, 至2001年四年的EDF進行實證研究,其中包括10只已退市或暫停上市股票,我們稱為樣本1;10只已連續2年或3年嚴重虧損的股票,稱為樣本2和10只績優股,稱為樣本3,從而把樣本分為三個子樣本。我們假定無風險利率r和資產市場價值的回報率\mu都為5%,時間範圍!為一年,違約點為負債總額。
由於篇幅有限我們只列示了6只股票,結果如下:
表 樣本基本情況表 (單位:萬元)
| 樣本 | 公司 | 年份 | 股權市值 | 負債 | 總資產 | 股權市值波動率 | 資產市值波動率 | 資產市值 | 資產市值/總資產 | 違約距離(1) | EDF(1) | 違約距離(2) | EDF(2) |
| 樣本1 | ST九州 | 2001 | 29979 | 144768 | 17951 | 60.64% | 10.64% | 167488 | 9.33 | 1.27493 | 10.1167% | 1.78684 | 3.6981% |
| 2000 | 128026 | 140034 | 64737 | 45.18% | 23.18% | 261217 | 4.04 | 2.00162 | 2.2663% | 2.78986 | 0.2637% | ||
| 1999 | 108510 | 123109 | 136781 | 49.34% | 25.34% | 225562 | 1.65 | 1.79248 | 3.6528% | 2.46024 | 0.6942% | ||
| 1998 | 156569 | 57077 | 115797 | 36.44% | 29.84% | 210862 | 1.82 | 2.44369 | 0.7269% | 4.39697 | 0.0005% | ||
| ST海洋 | 2001 | 45535 | 54644 | 5915 | 53.16% | 25.76% | 97471 | 16.48 | 1.70595 | 4.4008% | 2.31228 | 1.0381% | |
| 2000 | 116289 | 36044 | 36896 | 42.79% | 34.59% | 150575 | 4.08 | 2.19889 | 1.3943% | 4.10478 | 0.0020% | ||
| 1999 | 62958 | 54364 | 73821 | 51.14% | 29.14%114650 | 1.56 | 1.80431 | 3.5592% | 2.58628 | 0.4851% | |||
| 1998 | 77324 | 48334 | 72604 | 43.64% | 28.44% | 123300 | 1.70 | 2.13761 | 1.6274% | 3.32609 | 0.0440% | ||
| 樣本2 | ST昆百大 | 52595 | 93584 | 104132 | 39.86% | 15.16% | 141610 | 1.36 | 2.2373 | 1.2633% | 2.9866 | 0.1410% | |
| 2000 | 77752 | 92460 | 11023 | 40.21% | 19.31% | 165699 | 1.50 | 2.2893 | 1.1030% | 3.1841 | 0.0726% | ||
| 1999 | 54129 | 95302 | 120730 | 41.06% | 15.66% | 144777 | 1.20 | 2.1817 | 1.4567% | 2.9104 | 0.1805% | ||
| 1998 | 54139 | 100595 | 126432 | 39.88% | 14.78% | 149822 | 1.18 | 2.2230 | 1.3107% | 2.9595 | 0.1541% | ||
| ST原宜 | 2001136897 | 24871 | 54756 | 25.08% | 22.18% | 160555 | 2.93 | 3.8110 | 0.0069% | 8.5247 | 0.0000% | ||
| 2000 | 136657 | 32366 | 75192 | 25.30% | 21.40% | 167446 | 2.23 | 3.7705 | 0.0081% | 7.8086 | 0.0000% | ||
| 1999 | 81094 | 28955 | 74516 | 37.35% | 28.55% | 108637 | 1.46 | 2.5688 | 0.5102% | 4.6633 | 0.0002% | ||
| 1998 | 110488 | 30367 | 77041 | 28.61% | 23.41% | 139374 | 1.81 | 3.3411 | 0.0417% | 6.6060 | 0.0000% | ||
| 樣本3 | 中興通訊 | 2001 | 732701 | 509210 | 804895 | 29.39% | 18.29% | 1217077 | 1.51 | 3.1802 | 0.0736% | 4.9463 | 0.0000% |
| 2000 | 916003 | 437116 | 632101 | 33.13% | 23.43% | 1331801 | 2.11 | 2.8674 | 0.2070% | 4.8515 | 0.0001% | ||
| 1999 | 697497 | 180109 | 336485 | 47.74% | 39.04% | 868822 | 2.58 | 2.0304 | 2.1158% | 3.9634 | 0.0037% | ||
| 1998 | 691434 | 123487 | 219447 | 41.66% | 36.46% | 808899 | 3.69 | 2.3238 | 1.0068% | 5.1094 | 0.0000% | ||
| 五糧液 | 2001 | 1010234 | 198563 | 668787 | 51.62% | 44.32% | 1199112 | 1.79 | 1.8829 | 2.9859% | 3.9490 | 0.0039% | |
| 2000 | 1487362 | 140970 | 460092 | 22.32% | 21.32% | 1621458 | 3.52 | 4.2852 | 0.0009% | 11.5840 | 0.0000% | ||
| 1999 | 1106310 | 149840 | 391890 | 54.30% | 48.90% | 1248843 | 3.19 | 1.7995 | 3.5969% | 4.1937 | 0.0014% | ||
| 1998 | 1425984 | 97293 | 274440 | 32.27% | 31.17% | 1518532 | 5.53 | 3.0030 | 0.1337% | 8.8210 | 0.0000% |
從上表可以看出:(一)股權市值波動率大於資產市值波動率,因為資產市值包括了股權市值與負債,而負債一般都大於零。資產市值大於賬面總資產和股權市值,但小於股權市值與負債總額之和;(二)各樣本的EDF值存在較大差異,而且EDF(1)值大於EDF(2)值,我們可以證明這一點並非總是成立的,只有在某些條件限制下才為真。
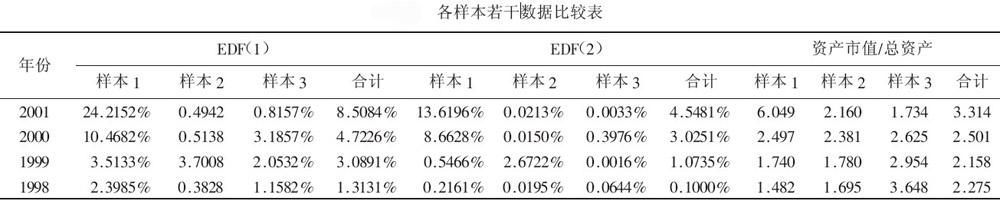
以下我們對全部30只股票作一概括:
從表2可以得出:
(一)樣本1的EDF值大於其他兩個樣本的值,說明EDF模型能在整體上區分已退市公司與其他類別公司。但模型不能區分樣本2與樣本3;
(二)樣本1的EDF值隨年份的增加而增加,說明隨著企業財務狀況的惡化,相應的違約率也隨之上升。樣本1的10只股票中,只有3只的EDF值變化無規律。對於樣本2,10只股票中有5只的EDF值隨著年份的增加而增加。至於樣本3,則沒有發現有明顯的規律之處。我們發現各樣本的EDF值都很小,但我們知道很多公司已經多年連續虧損,業績很差,其EDF值與其業績並不相符;
(三)資產市值與總資產的比例很大,而且業績越差的股票其比例越大。如樣本1,2001年整體比例有6倍之多。我們發現樣本!的比例隨著年份的增加而減少,樣本1和樣本2則隨著年份的增加而增加,說明績優股票自身價值比過去更趨合理化,而績差股票更加偏離其價值。
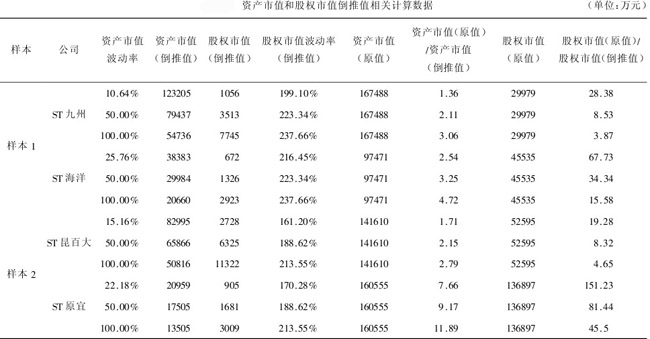
為了找出樣本1和樣本2的EDF值很小的原岡,我們發現對資產市值產生影響的變數有股權市值、股權市值波動率、無風險利率和違約點。一般來講無風險利率和違約點可以假設為常數,因而主要是股權市值和股權市值波動率對資產市值及其波動率產生影響。現假定樣本1和樣本2在2002年一年內的違約概率分別為95%、80%令其資產波動率分別為表1中計算出來的原實際資產波動率、50%和100%。從而在假設資產市值波動率已知的情況下,倒推出資產市值和股權市值。同樣限於篇幅我們只列示了 )只股票,結果如下:
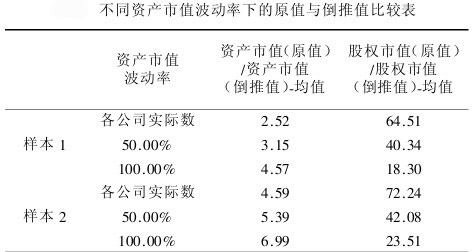
綜合(表3、表4)可以看出:
當資產市值波動率為原來實際數時,資產市值與資產市值(倒推值)的綜合比例樣本1為2.52倍,樣本2為)4.59倍。
即在我們假定樣本1、樣本2的違約概率分別為95%、80%,時計算出來的資產市值分別比原先計算的資產市值小2.52,倍4.59倍。因而各公司的資產市值存在高估現象。同時我們可以看出股權市值與股權市值(倒推值)的綜合比例樣本&為64.51倍,樣本2為72.24倍。我們認為正是股權市值的過高估值造成了資產市值的高估。當我們把樣本1和樣本2的資產波動率提高為50%和1005時,雖然股權市值(原值)與股權市值(倒推值)的比例都下降了,但仍然有20多倍。
- ↑ 鄭茂.基於EDF模型的上市公司信用風險實證研究[J].管理工程學報,2005,19(3)