貝葉斯決策法
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
決策的分類有很多種,如果按環境劃分,決策可以分為確定型、不確定型和風險型三大類,其中風險型決策是最常見的類型。風險型決策的主要特點是具有狀態發生 的不確定性。決策者面臨著幾種可能的狀態和相應的後果,且對這些狀態和後果得不到充分可靠的有關未來環境的信息,只能依據“過去的信息或經驗”去預測每種狀態和後果可能出現的概率,在這種情況下,決策者根據確定的決策函數計算出項目在不同狀態下的函數值,然後再結合概率求出相應的期望值,此值就是對未來可能出現的平均狀況的估計,決策者可以依此期望值的大小做出決策行為。常見的決策函數主要有成本函數、收益函數、效用函數。前面兩種函數是從貨幣因素考慮的,而後者是從非貨幣因素考慮的。這種以期望值為標準的分析法是決策者在處理風險型問題時常常使用的方法,貝葉斯決策法是最常見的以期望為標準的分析方法。它是在不完全情報下,對部分未知的狀態用主觀概率估計,然後用貝葉斯公式對發生概率進行修正,最後再利用期望值和修正概率做出最優決策。
如果決策函數是成本函數或收益函數,則決策者是從貨幣因素考慮問題的。貝葉斯決策模型是決策者在考慮成本或收益等經濟指標時經常使用的方法,它是在貝葉斯定理的基礎上提出來的。以收益型問題為例,其基本思想是在已知不確定性狀態變數θ的概率密度函數f(θ)的情況下,按照收益的期望值大小,對決策方案排序,則最優方案為使期望收益最大的方案。由於由貝葉斯定理可以推出通過抽樣增加信息量能夠使概率更加準確,概率準確則意味著決策風險的降低,所以貝葉斯定理保證了該決策模型的科學性。
1.收益函數的貝葉斯決策步驟
(1)計算出每種狀態的概率,計為Pi。
(2)對於收益型問題,列出條件收益的計算公式,求出在各種狀態下相應方案的條件收益CPij,結合概率求出相應的期望值EPij列出貝葉斯決策法收益表。
(3)通過貝葉斯決策法收益表,依次求出在各種狀態下可獲得的最大期望收益值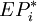 ,它們的和為該問題最理想的期望收益EPC,此時收益最大。
,它們的和為該問題最理想的期望收益EPC,此時收益最大。
(4)通過貝葉斯決策法收益表,求出各方案下的期望收益EMV,其中最大的值記為EMV * ,使期望收益最大的方案就是最優方案。ECC與EMV * 的差值表示完全情報價值,計為EVPI。
(5)寫出答案:最優方案a * =? EMV * =? EVPI=?
2.收益函數的貝葉斯決策模型舉例
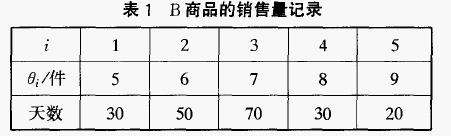
表1為某百貨商場過去200天關於商品B的日銷售量紀錄,商品B的進價為200元/f牛,售價為600元/f牛,如果當天銷售不完,餘下全部報廢,求該商品的最佳日訂貨量a * ,及相應的期望收益金額EMV * 和EVPI。
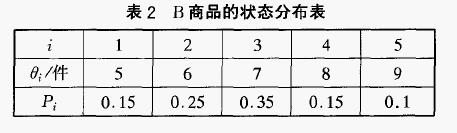
由表1可知,該商場商品B的銷售狀態空間為θ={θ1,θ1,θ1,θ1,θ1}={5,6,7,8,9},這些狀態發生的概率也可以推測出來,見表2。根據此狀態空間,決策者的決策空間為A={a1,a1,a1,a1,a1}={5,6,7,8,9}。
當商場的銷售量為θi,而進貨量為ai時,商場的條件收益為:
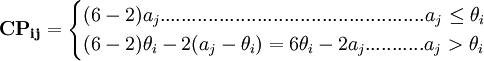
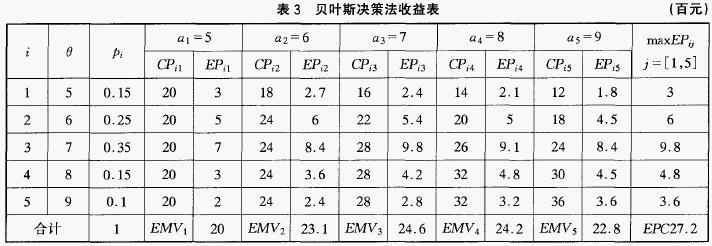
而相應的期望收益為EPij = CPij * PI,表3即為此例的貝葉斯決策法收益表:
從經濟角度看當日訂貨量等於日銷售量時,商場沒有因為多定貨或少定貨而造成的機會損失,因此獲得的收益最大,所以此例理論上的最大利潤為EPC=2,720元。但在實際工作中這個值很難得到,除非商場能夠根據情況隨時調整進貨量,因此商場的經營者往往追求的是期望收益的最大值,在此例中當訂貨量為7時期望收益最大,EMV * 和EVP,分別為2,460元和260元。
EVPI的含義為由於情報不准確而造成的商場的贏利損失,這個損失可能是因為銷售量小於7件而引發商品報廢產生的損失,也可能是因為銷售量大於7件使商場未能多盈利而造成的損失。商場若有百分之百準確的情報,則完全可以避免這類損失,因此定義EVPI為完全情報價值。
為了追求更多的利潤,決策者總是希望獲取一些準確信高的信息,現在隨著越來越多的咨詢公司、研究中心的出現,為我們獲取高質量的信息提供了可能。只要費用小於預期收入,決策者就可以考慮購買由信息公司提供的情報信息。這些信息主要是通過抽樣調查或其他途徑得到的概率,與憑藉經驗預測出來的概率不同它們的可靠性更高,這種概率稱為後驗概率,而前者稱為先驗概率。一般的用後驗概率代替先驗概率進行貝葉斯決策,往往可以得到更準確的方案,這種用後驗概率代替先驗概率再進行貝葉斯決策,就成為後驗分析法。需要指出的是有些情況下並非用後驗分析法就一定比先驗分析好,如果兩者選擇的方案相同,則意味著後者在增加成本的情況下收益並沒有增加,顯然此時先驗比後驗更加有效率。
決策者在進行決策時可以從貨幣因素出發進行決策,但因為決策的結果是由決策者承擔的,所以決策者個人的心理因素就會對決策的過程產生一定的影響。在眾 多心理因素中決策者對待風險的態度往往是決定性的因素。同樣的問題對於風險穩重者,為了少承擔風險,往往少訂商品以避免商品的積壓;而對於風險愛好者,他對未來的預期很高,則會冒險訂購較多的商品;而對待風險持中間型態度的決策者則往往只單純的從貨幣因素進行考慮。由於對風險的態度不同,所以不同的訂貨量給決策者所帶來的滿意程度也是不同的,而效用函數則可以表示這種不同。決策者會選取效用最大的方案作為候選方案。
1.效用函數決策步驟
(1)計算出每種狀態的概率,計為Pi。
(2)列出效用函數,求出在各種狀態下相應方案的效用值U(θi,ai),結合概率求出相應的期望值EUij,列出效用決策表。
(3)通過效用決策表,求出各方案下的期望效用EUi,其中最大的記為EU * ,使期望效用最大的方案就是最優方案。
(4)寫出答案:最優方案a * =?; EU * =?。
2.效用函數決策模型舉例
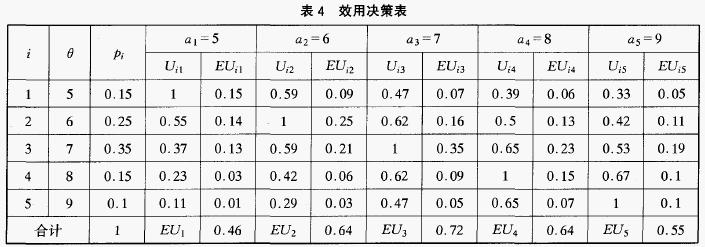
仍然討論上面的例子,假設決策者為風險穩重者,其效用值隨著日定貨量和日銷售量的差值的增大而減小,且當日定貨量等於日銷售量時,決策者最滿意,此時效用值為1,故假設效用函數為下式,據此可構建效用決策表(見表4)。
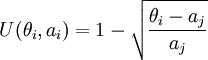
由表4可知,決策者的效用隨著定貨量與其加權平均和(6,8)的差距的加大而呈遞減趨勢,當定貨量是7時,決策者獲得最大的效用,即EU * = 0.72。可見此時的決策者屬於風險穩重者,需要說明的是最優方案的選取是與決策者當時所採用的效用函數有緊密聯繫的。
在上面討論的兩種方法中,都是按期望值的大小進行決策的。然而對於不同的方案,即使期望值相同,它們取值的離散程度仍然是不同的,顯然期望值大而離散程度小的方案是最優方案。為了考慮在單位期望值下不同方案的波動性的大小,決策者可以通過計算不同方案的變異繫數υ:
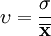
σ是標準差,而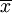 是期望值。在單位期望值下,變異繫數值小表示變數值密集,反之則表示變數值分散。
是期望值。在單位期望值下,變異繫數值小表示變數值密集,反之則表示變數值分散。
在上面的例子中,如果選擇第二種方法中的效用函數作為決策函數,則相應的變異繫數可以計算出來,分別為:0.578,0.347,0.278,0.195,0.282。其結果說明,在單位期望效用值下,方案a4的波動性最小。儘管方案a3的效用值較大,但是如果決策者從波動性的角度考慮,最優方案則應該是a4。
由於在生活當中許多自然現象和生產問題都是難以完全準確預測的,因此決策者在採取相應的決策時總會帶有一定的風險。貝葉斯決策法就是將各因素髮生某種變動引起結果變動的概率憑統計資料或憑經驗主觀地假設,然後進一步對期望值進行分析,由於此概率並不能證實其客觀性,故往往是主觀的和人為的概率,本身帶有一定的風險性和不肯定性。
雖然用期望的大小進行判斷有一些風險,但仍可以認為貝葉斯決策是一種兼科學性和實效性於一身的比較完善的用於解決風險型決策問題的方法,在實際中能夠廣泛應用於組織系統改革、企業效益、市場開發、證券投資等諸多領域。使用時根據決策者的側重點,結合變異繫數,綜合使用貨幣因素的貝葉斯決策、或效用函數的貝葉斯決策法,都會得到自己想要的結果。