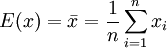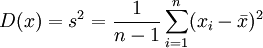統計推斷

出自 MBA智库百科(https://wiki.mbalib.com/)

統計推斷（Statistical Inference）

　　統計在研究現象的總體數量關係時，需要瞭解的總體對象的範圍往往是很大的，有時甚至是無限的，而由於經費、時間和精力等各種原因，以致有時在客觀上只能從中觀察部分單位或有限單位進行計算和分析，根據局部觀察結果來推斷總體。例如，要說明一批燈泡的平均使用壽命，只能從該批燈泡中抽取一小部分進行檢驗，推斷這一批燈泡的平均使用壽命，並給出這種推斷的置信程度。這種在一定置信程度下，根據樣本資料的特征，對總體的特征做出估計和預測的方法稱為統計推斷法。統計推斷是現代統計學的基本方法，在統計研究中得到了極為廣泛的應用，它既可以用於對總體參數的估計，也可以用作對總體某些分佈特征的假設檢驗。

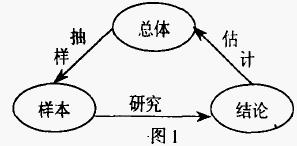
　　統計推斷是在概率論的基礎上依據樣本的有關數據和信息，對未知總體的質量特性參數，做出合理的判斷和估計。它的一般過程如圖l所示。

　　統計推斷有著廣泛的用途，幾乎遍及所有科學技術領域，在質量管理活動中應用尤其普遍。因此，討論統計推斷是一個十分有意義的課題。

　　為什麼我們不能直接研究對象的全部情況，而只能取得研究對象的部分信息來推斷和估計整體的某些規律呢？

　　1、在產品可靠性T程領域，研究某種產品在規定條件下和規定時間內完成規定功能的概率時，通常要做破壞性檢驗和試驗，如燈泡的壽命測試、焊縫的強度檢驗、電視機無故障工作時間的確定等。我們只能通過抽取樣本，對樣本進行破壞性試驗後，推斷總體的可靠性指標。如果對所有產品進行破壞性檢測，就沒有產品可供銷售了，這違背了我們研究的本來目的。

　　2、還有一些研究對象，組成其整體的個體是無限多的，客觀上對全部個體進行觀察和檢驗是根本不可能的。如研究海水中微生物的情況時，不可能將全部海水都裝入試管中；分析魚池中全部活魚的重量與長度時，不能將池水抽乾、逐條過秤等。因此，只能用隨機取樣統計推斷的方法。

　　3、有些情況對全部個體逐一研究、檢測是可以的，但需要付出非常多的財力、物力和時間。如自動化流水作業的生產過程，對每個產品進行檢測需要停機等。因此，我們也只能依賴於抽樣檢驗和調查，分析樣本後對整體做出判斷。

　　4、由於整體的不均勻性和樣本的隨機性，利用分析樣本得到的數據來推斷總體的情況必然會產生偏差。但是，在大多數情況下這種估計誤差的存在是合理的，也是可以容忍的。因為不同的問題有不同的精度要求，並不是所有問題都需要一個絕對準確的估量，也不是一切問題都能得到一個非常精確的結果，所以統計推斷是不可缺少的研究手段。

　　在質量活動和管理實踐中，人們關心的是特定產品的質量水平，如產品質量特性的平均值、不合格品率等。這些都需要從總體中抽取樣本，通過對樣本觀察值分析來估計和推斷，即根據樣本來推斷總體分佈的未知參數，稱為參數估計。參數估計有兩種基本形式：點估計和區間估計。

　　1、點估計

　　用樣本的統計量去估計總體相應未知參數稱為點估計。當我們任意抽取一個樣本：x₁、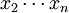，該樣本的均值E(x)和方差D(X)便已知：

　　如果已知該樣本所屬總體的分佈犁式，則可利用總體分佈型式均值和方差的計算公式推斷其分佈的未知參數。如表l所示。

二項分佈B(N,P)	泊松分佈P(λ)	均勻分佈U(a,b)	正態分佈N(μ,σ2)

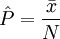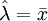　　對於同一總體，隨著抽取樣本的不同，就可得到不同的樣本均值和方差，通過計算．同一總體分佈未知參數就可產生多個估計值。這樣，就存在對眾多點估計優良性的評價問題。通常用無偏性和有效性作為評價點估計優良性的標準。即如果所有估計量的均值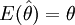，稱這些估計量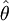為參數θ的無偏估計，在多個無偏估計量中方差小的估計量則更為有效。

　　2、區間估計

　　用樣本確定兩個統計量，構築一個置信水平為1 − α的區間，對總體未知參數給出估計，稱為區間估計。如果從正態總體中抽取一個樣本：x₁、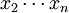，其樣本的均值為：

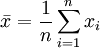
　　方差為：

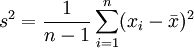
　　則該正態總體均值、方差和標準差的1 − α置信估計區間如表2所示。

　　點估計僅僅給出未知參數的一個具體估計值，沒有給出估計的精度，而區間估計卻體現了估計的精度。所謂置信水平1 − α，是指所構造的置信區間覆蓋未知參數的概率為1 − α。由於置信區間是由選用樣本的統計量構築的，它是會隨著樣本的變化而變化的，它有時覆蓋未知參數，有時卻沒有覆蓋未知參數。但是，用此法構築的置信區間，在100次中大約有100(1 − α)個區間覆蓋未知參數。

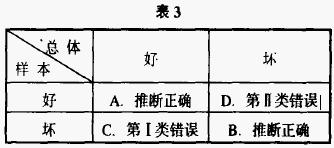
　　人們總是希望不犯錯誤，但是在統計推斷過程中不犯錯誤是不可能的。由於總體的不均勻性和樣本的隨機性，統計推斷必然存在風險(錯誤)。假設有一批未知質量狀況的產品，現在隨機抽取其中的一個樣本，通過檢驗、分析樣本的質量狀況，來推斷整批產品的質量好壞，則可能出現如表3所示的四種情況。

　　A、假定這批產品質量是好的，通過檢驗樣本發現樣本質量也是好的，則推斷該批產品質量好而決定接收。顯然，這個統計推斷是完全正確的。B、假定這批產品質量不好，通過檢驗發現樣本質量不好，則推斷該批產品質量不好而拒收。該統計推斷結論也是合理的。C、如果該批產品質量是好的，而通過檢驗樣本發現樣本質量是壞的，則推斷該批產品質量不好而拒收，就犯了“棄真”的錯誤，習慣上把它稱做第Ⅰ類錯誤。D、如果該批產品質量不好，通過檢驗樣本發現樣本質量是好的，則推斷該批產品質量好而予以接收，則犯了“取偽”的錯誤，通常將其稱做第Ⅱ類錯誤。

　　犯錯誤就會造成損失，就會發生預測失誤、判斷失誤，就會導致不希望結果的發生。在統計推斷過程中上述兩類錯誤總是此漲彼消不可避免的，我們的原則是控制兩類錯誤帶來的損失最小且已知。

　　在不同的統計推斷過程中，對上述兩類錯誤有著不同的描述。在用控製圖進行統計過程式控制制中，第Ⅰ類錯誤叫“虛發警報”，即生產正常而點子偶然超出控制界限，依此就判異而犯“棄真”錯誤；第Ⅱ類錯誤叫“漏發警報”，即過程已經異常，有部分點子仍位於控制界限內。依此判過程正常而犯“取偽”錯誤。在抽樣檢驗過程中，第Ⅰ類錯誤為生產方風險，即對於給定的抽樣方案，當質量水平為某一指定的可接收質量時被拒收的概率，此時生產方遭受損失；第Ⅱ類錯誤為使用方風險，即對於給定的抽樣方案，當質量水平為某一指定的不滿意質量時被接收的概率，此時使用方承受損失。在假設檢驗過程中，犯兩類錯誤的情況如表4。

　　當原假設H₀成立時，由於樣本觀察值落人拒絕域W中而誤認為H₀不成立，犯“棄真”錯誤；當原假設H₀實際上不成立，由於樣本觀察值未落人拒絕域W而誤認為H₀成立，犯“取偽”錯誤。

　　個體是總體的一部分，局部的特性能反映全局的特點，但是，由於總體的不均勻性和樣本的隨機性，又使得樣本不能精確地反映總體。因此，抽取部分個體經分析得出有關總體的結論存在著差錯和不可靠。從理論上講有兩種途徑可以消除和減少這種差錯。其一，使總體最大限度地均勻。總體是我們要研究的未知事物，我們往往不可能改變他的均勻性，當能夠使其達到理想的均勻時，已經完全掌握了它，沒有研究的必要了。其二，採取適當的抽樣方法確保抽樣的“代表性”，可有效地控制和提高統計推斷的可靠性和正確性。

　　隨機抽樣的方法很多，常用的有：

　　1、簡單隨機抽樣

　　簡單隨機抽樣，是指抽樣過程應獨立進行並且總體中每個個體被抽到的機會均等。隨機抽樣不是隨便抽取，隨便抽取容易受到個人好惡的影響。為實現隨機化，可採取抽簽、擲隨機數骰子或查隨機數值表等辦法。如從100件產品中隨機抽取l0件組成樣本，可以把這100件產品從l開始編號直到100號，然後用抓鬮的辦法任意抽出l0個編號，由這l0個編號代表的產品組成樣本。此種抽樣方法的優點是抽樣誤差小，缺點是手續繁雜。在實踐中真正做到每個個體被抽到的機會相等是不容易的。

　　2、周期系統抽樣

　　周期系統抽樣，又叫等距抽樣或機械抽樣，即將總體按順序編號，用抽簽或查隨機數值表的方法確定首件，進而按等距原則依次抽取樣本。如從120個零件中取五個做樣本，先按生產順序給產品編號，用簡單隨機抽樣法確定首件，然後按每隔24(由120÷5=24得)個號碼抽取一個，共抽取五個組成樣本。這種方法特別適用於流水線上取樣，操作簡便，實施起來不易出現差錯。但抽樣起點一經確定，整個樣本就完全固定。對總體質量特性含有某種周期性變化，而當抽樣間隔恰好與質量特性變化周期吻合時，就可能得到一個偏差很大的樣本。

　　3、分層抽樣法

　　分層抽樣法，即從一個可以分成不同子總體的總體中，按規定比例從不同層中隨機抽取個體的方法。當不同設備、不同環境生產同一種產品時，由於條件差別產品質量可能有較大差異，為了使所抽取的樣本具有代表性，可以將不同條件下生產的產品組成組，使同一組內產品質量均勻，然後在各組內按比例隨機抽取樣品合成一個樣本。這種抽樣方法得到的樣本代表性比較好，抽樣誤差較小，缺點是抽樣手續較繁，常用於產品質量檢驗。

　　4、整群抽樣法

　　這種方法是先將總體按一定方式分成多個群，然後隨機地抽取若幹群並由這些群中的所有個體組成樣本。如按照生產過程將1000個零件分別裝入2O個箱中，每箱5O個，然後隨機抽取一箱，此箱中5O個零件組成樣本。這種抽樣方法實施方便，但樣本來自個別群體而不能均勻分佈在總體中，因而代表性差，抽樣誤差較大。