灰數統計方法
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
灰數統計方法是以灰數的白化函數生成為基礎,將一些具體數據按某種灰類所描述的類別進行歸納整理,從而來加強對事物認識的一種方法[1]。
灰元、灰數、灰關係是灰色現象的特征，是灰色系統的標誌。而灰數又是灰色系統的內核。在技術系統、經濟系統、社會系統、教育系統和管理等系統中，人們對某待評項目(指標)的評價不僅包含著許多不確定性、隨機性和模糊性，而且涉及到心理因素，故有灰內話。同一評價者在不同次的評定中可能給出不同的結果，不同的評價者其結果可能差異更大，而且在評價中也很難獲得一個確切的值(數)，評價者往往用“大約是多少”，“在多少到多少之間”，甚至是“差不多” ，“比較可靠”等方式表達他們的估計。這樣的結果值以其內涵被定義為灰數。對這些灰數進行統計分析，一般的方法無能為力，因此而尋求一種方法分析估價這些評價，以減少評價誤差。灰數統計原理和方法為解決這類同題提供了科學方法。
灰數統計方法的內容及原理[2]
以某風險性指標(以c表示)的風險性大小為例，選n個評價者在軸
上10個等級上給出估計。人們通常不能確定地說是多少，而常給出類似[O.5，0.7]之間的估計，這就是說對於任一評價者來說，雖然不能給出一個確定的點，但其評價總會穩定在一個區間內，記為[O．5，0．7]，k表示第k個評價者。若有n個評價者便可得到n個區間值，形成一個灰數統計序列：
[
],![[u_1^{(2)},u_2^{(2)}]](/w/images/math/4/6/c/46cd00572cac192325ca165ca893477e.png)
,...,![[u_1^{(n)},u_2^{(n)}]](/w/images/math/d/6/c/d6c93af5e0e3b95f460268c2f54a7d17.png)
這n個小子集疊加在一起則形成覆蓋在評價值軸上的一種分佈：
這種分佈可用下式描述：
![\bar{X}_(u)=\frac{1}{n}\sum_{k=1}^n X[u_1^{(k)},u_2^{(k)}]^{(n)}](/w/images/math/b/6/0/b60deaa776e94ecbeb3b8a35a98134db.png)
(1)
其中：
![X[u_1^{(k)},u_2^{(k)}]^{(n)}=\begin{cases} 1,& u_1^{(k)}\le u\le u_2^{(k)}\\0,& \mbox{other}\end{cases}](/w/images/math/e/3/8/e38d882f993d467083df805f9c55591a.png)
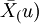被稱為樣本落影函數，那麼指標c的評價值取為：
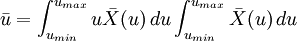(2)
其中umin和umax分別為指標c可能的最高、最低取值。可以證明：
![\int_{u_{min}}^{u_{max}} \bar{X}(u)\,du=\frac{1}{n}\sum_{k=1}^n[u_2^{(k)}-u_1^{(k)}]](/w/images/math/c/4/8/c48512374b52e8bd6ea4b64839a85492.png)
(3)
![\int_{u_{min}}^{u_{max}} \bar{X}(u)\,du=\frac{1}{2n}\sum_{k=1}^n[[u_2^{(k)^2}-(u_1^{(k)})^2]](/w/images/math/e/1/4/e143549a885758393d5da0e2d99da667.png)
(4)
則:
![\bar{u}=\frac{1}{2}\sum_{k=1}^n[(u_2^{(k)})^2-(u_1^{(k)})^2]/\sum_{k=1}^n[u_2^{(k)}-u_1^{(k)}]](/w/images/math/3/b/0/3b031866441c3783d318a81e43126ac2.png)
(5)
事實上，它不僅處理不確切的評價，而且很方便地集中了多種意見或試驗結果，減少了評價中的隨機誤差．更重要的是它可以充分利用評價過程中的信息．除獲得了評價值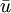
外，還可通過分析
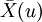獲得評價者對指標的把握度。
a．當指標可以準確定量時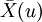，是一個常數1。如圖1-a，說明評價者對指標的把握度最大。
b．當 次試驗或n個區間估計很不集中時，說明評價者對指標的把握程度較小．此時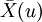的形狀比較扁平(圖1-b)。
c．當 n個評價區間的分佈比較集中，則說明評價者對指標的把握程度較高。此時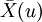的形狀比較尖瘦(圖1-c)。
以上分析表明n次試驗結果分佈的集中程度，即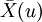形狀的“胖瘦”反映了評價者對指標的把握度。完全有把握，意見一致，評價值非常集中。把握不大，意見就不一致，評價值就比較分散．於是根據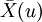我們可分析指標評價的可靠程度。定義
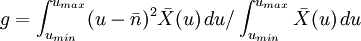(6)
可以證明：
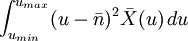=![\frac{1}{3n}\sum{k=1}^n[(u_2^{(k)}-\bar{u})^3-(u_1^{(k)}-\bar{u})^3]](/w/images/math/f/7/f/f7fff5a0a9a1e5760f0214c982647854.png)
(7)
有式（7）和式（3）有
![g=\frac{1}{3}\sum_{k=1}^n[(u_2^{(k)}-\bar{u})^3-(u_1^{(k)}-\bar{u})^3]/\sum_{k=1}^n[(u_2^{(k)}-u_1^{(k)}]](/w/images/math/f/5/a/f5afc7a3189d6f769436afb147980552.png)
(8)
則很明顯，g越大，評價者對指標的把握度越小，指標價值的可靠程度也就越低，故有定義：指標c(第i個指標)的置信度bai為指標評價值可靠程度的一種度．評價值可靠程度越大，指標置信度越高。
bai = 1 / (1 − gi) (9)
然而，由於每個指標都得到一個bi，故定義指標總置信度為：
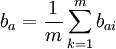(10)
