檢驗效能
出自 MBA智库百科(https://wiki.mbalib.com/)
檢驗效能(power of test)
目錄 |
什麼是檢驗效能[1]
檢驗效能或把握度,是指兩總體確有差別,按α水準能發現它們有差別的能力。用1-β表示其概率大小。
檢驗效能的估計[1]
檢驗效能只取單側,一般認為檢驗效能至少取0.80。β表示第二類錯誤的概率,其大小很難確切估計。一般藉助於求uβ,再查u值表估計β,然後求1-β。
假設檢驗結果出現P>α時,則不拒絕檢驗假設H0,稱差別無統計學意義,臨床常叫“陰性”結果。但“陰性”結果有兩種可能:①β較小,即1-β較大,或當樣本含量n>400時,就認為被比較的指標間很可能無差別。②β較大,即1-β較小,如小於0.80(也有學者認為小於0.70),且n<400時,便認為所比較的指標間很可能差異有統計學意義,由於樣本含量不足未 能發現,是“假陰性”結果。因此在估算樣本含量時,要考慮檢驗效能。部分計算uβ的公式是由樣本含量估算式、通過恆等變換導出,故統計符號與意義均相同。
常用計算uβ的公式如下。
1.兩樣本均數比較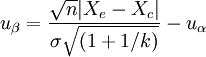 (1)
(1)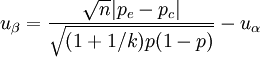 (2)
(2)3.病例對照研究
非配對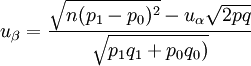 (3)
(3)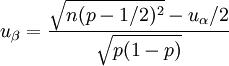 (4)
(4)![u_\beta=\frac{[n(p_1-p_0)^2]-u_\alpha[(1+1/c)pq]^{1/2}}{[p_0q_0+p_1q_1/c]^{1/2}}](/w/images/math/0/2/a/02aa0b72993e6891e9c6cc3975e97a0f.png) (5)
(5)例1 某醫師研究藥物對宮縮及外陰創傷的鎮痛效果,若新藥組觀察40例、鎮痛率 75%,舊藥組觀察60例、鎮痛率55%,當單側U0.05 = 1.6449,問該試驗檢驗效能如何?
本例試驗組有效率pe = 0.75、樣本含量ne = 40;對照組有效率pc = 0.55、樣本含量nc = 60,平均有效率P=(40×0.75+60×0.55)/(40+60)=0.63;k=60/40=1.5,又試驗組n=40、對照組kn=60,已知U0.05 = 1.6449,代入式(2),得: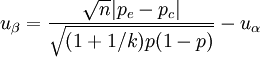 (2)
(2)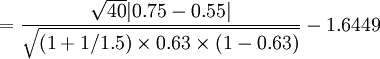
以uβ = 0.3845查u值表,得0.40>β>0.30,即0.60<1-β<0.70。故該試驗檢驗效能為0.60~0.70,可認為該試驗檢驗效能小,與樣本含量不足有關。
檢驗效能的決定因素[2]
檢驗效能的大小主要與以下四個因素有關。
(1)總體差別的大小:正確選擇被試因素及其水平,這是實驗成敗的首要環節。被試因素的有效性越強,H0與H1涉及的不同總體均數之間的差距越大,兩者在分佈上的重疊面積就越小。由於β較小,1-β就必然較大。
(2)檢驗水準(α)的大小:通常H0與H1兩個總體存在一定的重疊面積,界值移動必然引起α與β同時改變。由於α與β存在反變關係,故通過增大口值可提高檢驗效能1-β。然而假設檢驗的目的大多是希望提示被試因素有效性高,應當要求d值越小越好;若將α值過分增大,顯然是不恰當的。相反,如將α過分縮小,勢必引起β增大,檢驗效能降低。因此,在實驗設計時,必須合理地兼顧α與β。在通常情況下,實驗設計時α取0.05,β取0.10或0.05。
(3)標準差的大小:由於α與β呈反比,兩全其美的方法就是使兩個相互比較的總體分佈都很集中,重疊面積縮小,這樣就可收到α與β均減小的效果。在兩個總體均數與樣本含量固定的條件下,各總體分佈的面積不變,但其擴布範圍與標準差成正比。因此,儘量減小個體差異,嚴格控制實驗條件,認真遵守操作規程,努力使標準差減小到合理水平,這是提高檢驗效能的重要途徑之一。
(4)樣本含量的多少:在兩總體均數與標準差固定的條件下,儘管總體分佈的擴布範圍不變,但隨著樣本含量(n)增大,標準誤縮小,總體分佈趨向集中,α與β都減小,因而檢驗效能增加。所以,對於提高檢驗效能而言,增大樣本含量,這也是一種兩全其美的辦法。在理論上,任何真實存在的差異不論大小與有無實際意義,只要有足夠大的咒,通過假設檢驗都可以檢出具有統計意義。然而在科研中必須首先考慮差異程度的實際意義,不能盲目地擴大樣本含量。同時也應看到:樣本含量由n增大至m倍(即m×n),標準誤僅縮小至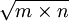 倍。例如,樣本含量由n增至9n,標準誤
倍。例如,樣本含量由n增至9n,標準誤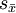 僅減至原來的1/3。因此,通過增大n來提高檢驗效能,其代價是相當高的,在數量上必須適可而止。
僅減至原來的1/3。因此,通過增大n來提高檢驗效能,其代價是相當高的,在數量上必須適可而止。
檢驗效能的意義[3]
檢驗效能,又稱假設檢驗的功效(power of a test),用1-β表示,其意義是,當所研究的總體與H0確有差別時,按照檢驗水準α能夠發現它(拒絕H0)的概率。若1-β=0.90,則意味著當H0不成立時,理論上在100次抽樣實驗中,在α檢驗水準上平均有90次能拒絕H0。檢驗效能可用小數(或百分數)表示,一般取0.99、0.95、0.90、0.80、0.50。研究中要求的檢驗效能越高,所需的樣本含量也越大。樣本含量、客觀事物差異的大小、個體間變異的大小和α值都是影響檢驗功效的要素。當樣本含量固定時,α與β呈反向變化的關係,即α增大,β減小,反之亦然;若欲同時減小α與β,則只有增加樣本含量。因此,若要增大檢驗效能(增大1-β,減小β),一是增大α,二是增大樣本含量。
檢驗效能雖然不是設計時需要解決的,但在查閱文獻和借鑒前人經驗時應當認真考慮。當假設檢驗根據P>0.05做出無統計學意義的結論時,研究者則面臨著犯Ⅱ型錯誤的可能性,應當考慮是否總體間的差異確實存在,但由於檢驗效能不足而未能把該差異反映出來。








第一行的概念錯了是按啊發 發現其差異的能力不是。貝塔