洛倫茲曲線
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
洛倫茲曲線(Lorenz curve),也譯為“勞倫茲曲線” 就是,在一個總體(國家、地區)內,以“最貧窮的人口計算起一直到最富有人口”的人口百分比對應各個人口百分比的收入百分比的點組成的曲線。洛倫茲曲線研究的是國民收入在國民之間的分配問題,美國統計學家(或說奧地利統計學家)M.O.洛倫茲(Max Otto Lorenz,1903- )1907年(或說1905年)提出了著名的洛倫茲曲線。義大利經濟學家基尼在此基礎上定義了基尼繫數。
畫一個矩形,矩形的高衡量社會財富的百分比,將之分為五等份,每一等分為20的社會總財富。在矩形的長上,將100的家庭從最貧者到最富者自左向右排列,也分為5等分,第一個等份代表收入最低的20的家庭。在這個矩形中,將每一百分的家庭所有擁有的財富的百分比累計起來,並將相應的點畫在圖中,便得到了一條曲線就是洛倫茲曲線。
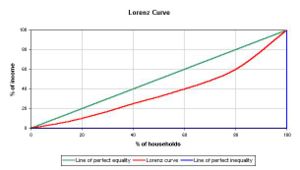
顯而易見,洛倫茲曲線的彎曲程度具有重要意義。一般來說,它反映了收入分配的不平等程度。彎曲程度越大,收入分配程度越不平等;反之亦然。特別是,如果所有收入都集中在某一個人手中,而其餘人口均一無所有,收入分配達到完全不平等,洛倫茲曲線成為折線OHL;另一方面,如果任一人口百分比等於其收入百分比,從而人口累計百分比等於收入累計百分比,則收入分配就是完全平等的,洛倫茲曲線成為通過原點的45度線OL。
洛倫茲曲線用以比較和分析一個國家在不同時代或者不同國家在同一時代的財富不平等,該曲線作為一個總結收入和財富分配信息的便利的圖形方法得到廣泛應用。
圖中橫軸OH表示人口(按收入由低到高分組)的累積百分比,縱軸OM表示收入的累積百分比,弧線OL為洛倫茲曲線。
洛倫茲曲線的彎曲程度有重要意義。一般來講,它反映了收入分配的不平等程度。彎曲程度越大,收入分配越不平等,反之亦然。特別是,如果所有收入都集中在一人手中,而其餘人口均一無所獲時,收入分配達到完全不平等,洛倫茲曲線成為折線OHL.另一方面,若任一人口百分比均等於其收入百分比,從而人口累計百分比等於收入累計百分比,則收入分配是完全平等的,洛倫茲曲線成為通過原點的45度線OL。
一般來說,一個國家的收入分配,既不是完全不平等,也不是完全平等,而是介於兩者之間。相應的洛倫茲曲線,既不是折線OHL,也不是45度線OL,而是像圖中這樣向橫軸突出的弧線OL,儘管突出的程度有所不同。
將洛倫茲曲線與45度線之間的部分A叫做“不平等面積”,當收入分配達到完全不平等時,洛倫茲曲線成為折線OHL,OHL與45度線之間的面積A+B叫做“完全不平等面積”。不平等面積與完全不平等面積之比,成為基尼繫數,是衡量一國貧富差距的標準。基尼繫數G=A/(A+B).顯然,基尼繫數不會大於1,也不會小於零。
洛倫茲曲線的方法[1]
儘管可根據收入分配的統計數據加以描繪,但至今卻未能找到一種有效的方法,準確地擬合洛倫茲曲線方程並由此求出精確的基尼繫數。目前常被使用的方法主要有三種:
(1)幾何計演算法。即根據分組資料,按幾何圖形分塊近似逼近計算的方法。
(2)間接擬合法。即先擬合求出收入分配的概率密度函數,再根據概率密度函數導出洛倫茲曲線。
(3)曲線擬合法,即選擇適當的曲線直接擬合洛倫茲曲線,常用的曲線有二次曲線、指數曲線和冪函數曲線。
利用第一種方法不能得到洛倫茲曲線的表達式,只能用來計算基尼繫數,但由於在計算分塊面積時用直線近似地代替曲線,所估計的基尼繫數要小於實際值,尤其在數據點較少時,誤差較大。第二種方法由於計算收入分配的概率密度的複雜性,很難提出合適的概率函數。至於第三種方法,即直接用曲線方程去擬合洛倫茲曲線,應該不失為一種較好的方法,但目前主要的問題在於現有常用的曲線並不適用,曲線含義不明確,或擬合誤差較大。
為了更準確地描述洛倫茲曲線和精確地估計基尼繫數,我們通過分析洛倫茲曲線的特性,設計出一條洛倫茲曲線方程,對洛倫茲曲線直接進行擬合。經過實例分析,擬合效果好,由洛倫茲曲線可推導出基尼繫數的計算公式,計算結果精確度也很高。
概率密度函數(f(x))或累積分佈函數(F(x)):
洛倫茲曲線方程[1]
設收入變數的概率為f(Y),總人口數為N,則收入等級在Y到Y+dY內人口數的概率為f(Y)dY,在該收入級內的人口數為Nf(Y)dY,這樣收入少於Y的累積人口數占總人口數的百分比。
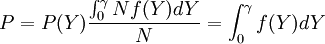 (1)
(1)
式中P(Y)表示收入少於Y的人口分佈函數。
收入少於Y的所有人的累積收入在總收入中的份額為
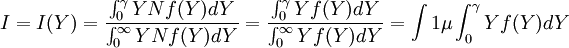 (2)
(2)
式中I(Y)表示收入少於Y的所有人的收入的分佈函數;為收入的期望值或社會總平均收入。
因此,I(Y)和P(Y)的函數關係即洛倫茲曲線方程可表示成
I=I(P)(3)
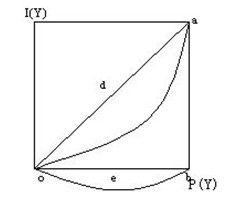
從上圖中可以看到,洛倫茲曲線oca可以看成是45°對角線oda和弓形曲線oeb的合成曲線。
現設計弓形曲線oeb的方程為
I = − APα(1 − P)β(4)
這條方程能根據繫數α和β的調整反映不同偏向的弓形曲線。
當α>β時,弓形曲線偏向右邊;當α<β時,弓形曲線偏向左邊。45°對角線oda的方程為
I=P(5)
將這兩條方程合成,即得到合成曲線的方程即洛倫茲曲線的方程
I = P − APα(1 − P)β(6)
式中:A、α、β為繫數;P為按收入等級分組的累計人口數占總人口比例,0≤P≤100;I為累計人口數比例為P的所有人的累積收入在總收入中的份額,0≤I≤100。
作為洛倫茲曲線,要求滿足如下四個特性:
(1)洛倫茲曲線滿足特殊點的數值,即當P=0時,I=0,表示0%的人口其收入為0;P=I時,I=1,表示100%的人口其收入為100%;
(2)洛倫茲曲線處於絕對平等線oda下方,絕對不平等線oba上方;
(3)洛倫茲曲線是遞增的;
(4)洛倫茲曲線是下凸的。
第一個、第二個特性要求(6)式中的A>0,以及α>0,β>0;第三個特性要求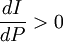 ,第四個特性要求
,第四個特性要求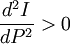 。
。
現在對(6)式求I關於P的一階導數和二階導數:
![\frac{dI}{dP}=1-A\left[\alpha P^{\alpha-1}(1-P)^\beta-\beta P^\alpha(1-P)^{\beta-1}\right]](/w/images/math/8/8/f/88f5384d21cffcc38cc30c5891102e82.png)
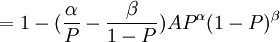
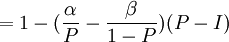
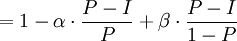 (7)
(7)
![\frac{d^2 I}{dP^2}=(P-I)\left[\frac{\alpha(1-\alpha)}{P^2}+\frac{\beta(1-\beta)}{(1-P)^2}+\frac{2\alpha \beta}{P(1-P)}\right]](/w/images/math/7/2/c/72c5c0aed7303b0609c0a8509d1aa184.png)
![=AP^\alpha(1-P)^\beta\left[frac{\alpha(1-\alpha)}{P^2}+\frac{\beta(1-\beta)}{(1-P)^2}+\frac{2\alpha \beta}{P(1-P)}\right]](/w/images/math/d/1/a/d1ae20f536ca40954fdb8467f3eb8754.png) (8)
(8)
容易證明,當A>0,0<α<1,0<β<1時,(6)式滿足了洛倫茲曲線的四個特性。因此,滿足洛倫茲曲線所有特性的充分條件是A>0,0<α<1,0<β<1,將(6)式轉換成如下形式
ln(P − I) = lnA + αP + βln(1 − P)(9)
這樣,根據I和P的統計數據,利用最小二乘法便可估計出參數A、α、β值。
洛侖茲曲線的性質[2]
洛侖茲曲線具有以下的性質:
(1)P(0)=0,Q(0)=0,即0%的人口的收入占總收入的0%;而P(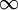 )=1,Q(
)=1,Q(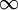 )=1,即100%的人口的收入占總收入的100%。
)=1,即100%的人口的收入占總收入的100%。
(2)洛侖茲曲線是遞增的,因為

(3)洛侖茲曲線是下凸的,因為
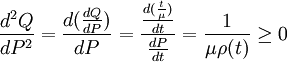
(4)當洛侖茲曲線為45°角的0A線時,人口比重增加一個單位,相應的收入比重也增加一個單位,這表明每個人的收入相同,即收入分配是絕對平均的.直線0A成為絕對平均線.
(5)當洛侖茲曲線為0BA折線時,人口比重在增加到100%前,收入比重保持0不變,當人口比重一達到100%.收入比重馬上達到100%,這表明所有收入集中在一個人手中,而其他人的收入都為零,即社會收入分配是絕對不平均的.0BA折線稱為絕對不平均線。
(6)由性質(1)、(2)可見“洛侖茲曲線其實是一條分佈曲線,洛侖茲函數Q=Q(P)是一個分佈函數.
顯然,在現實生活中,資本在各經濟部門之間的分配絕對平均化或絕對不平均這2種極端現象是不存在的;相反,不均等,有差異是普遍存在的,也是正常的,一般情況是介於二者之間.即洛侖茲曲線是一條介於絕對平均線和絕對不平均線之間的一條曲線。
案例一:洛倫茲曲線的案例分析[1]
利用國家統計局抽樣調查的1997年城鎮居民全部收入資料進行分析
| 收入分組 | 人口比重 | 收入比重 | 累計人口比重(P) | 1-P | 累計收入比重(I) | P-I |
| 最低收入戶 | 0.1129 | 0.0535 | 0.1129 | 0.8871 | 0.0535 | 0.0594 |
| 低收入戶 | 0.1078 | 0.0675 | 0.2207 | 0.7793 | 0.1210 | 0.0997 |
| 中等偏下戶 | 0.2094 | 0.1611 | 0.4301 | 0.5699 | 0.2821 | 0.1480 |
| 中等收入戶 | 0.2000 | 0.1899 | 0.6301 | 0.3699 | 0.4720 | 0.1581 |
| 中等偏上戶 | 0.1925 | 0.2255 | 0.8226 | 0.1774 | 0.6975 | 0.1251 |
| 高收入戶 | 0.9222 | 0.1332 | 0.9148 | 0.0852 | 0.8307 | 0.0841 |
| 最高收入戶 | 0.853 | 0.1693 | 1.0000 | 0.0000 | 1.0000 | 0.0000 |
註:本表數據根據《中國統計年鑒1998年》整理計算
根據上表中所給出的數據(因計算的要求,去掉最後一行數據),利用最小二乘法,對(9)式進行估計,得到如下結果
ln(P − I) = − 0.7748 + 0.9040lnP + 0.652ln(1 − P)(10)
(144.8763) (118.5231)
R2=0.9999 D.W.=2.6020
(10)式下麵括弧內的數字為t統計量,R2為擬合繫數,D.W.為德賓-沃森檢驗值。由估計結果可知,(10)式回歸繫數均通過統計檢驗(取顯著性水平α=0.01),D.W.值也表明不存在序列相關。
(10)式可寫成(6)式的洛倫茲曲線形式:
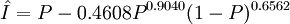 (11)
(11)
由於上式A=0.4608>0,0<α,β<1,滿足洛倫茲曲線的特性要求,故(11)式作為洛倫茲曲線的估計式具有明確的含義,且擬合效果相當好。下表給出了誤差分析情況,收入比重的估計值和累計收入比重的估計值的平均相對誤差僅為0.07和0.34,估計精度相當高。我們利用(6)式對不同的例子進行了多次試算,同樣都達到了理想的擬合效果,說明洛倫茲曲線方程具有很高的實用價值。
| 收入分組 | 累計收入比重實際值I | 累計收入比重估計值 \hat{I} | 相對誤差(%) | 收入比重實際值 | 收入比重估計值 | 相對誤差(%) |
| 最低收入戶 | 0.0535 | 0.0535 | 0.00 | 0.535 | 0.0535 | 0.00 |
| 低收入戶 | 0.1210 | 0.1209 | 0.08 | 0.675 | 0.0674 | 0.15 |
| 中等偏下戶 | 0.2821 | 0.2815 | 0.21 | 0.1611 | 0.1606 | 0.31 |
| 中等收入戶 | 0.4720 | 0.7421 | -0.02 | 0.1899 | 0.1966 | -0.37 |
| 中等偏上戶 | 0.6975 | 0.6984 | -0.13 | 0.2255 | 0.2263 | -0.35 |
| 高收入戶 | 0.8307 | 0.8303 | 0.05 | 0.1332 | 0.1309 | 0.98 |
| 最高收入戶 | 1.0000 | 1.0000 | 0.00 | 0.1693 | 0.1609 | 0.24 |
| 平均值 | - | - | 0.07 | - | - | 0.34 |
計算出基尼繫數
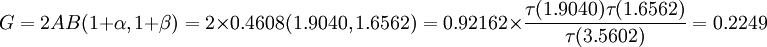
案例二:用洛倫茲曲線分析銷售結構[3]
一、分析銷售結構的傳統方法
連鎖業經營的重要特點是集中統一控制,總部的決策是建立在對來自第一線各業務部門的數據上的,快速準確地抽取大量數據中的信息是連鎖管理的必然要求使用管理信息系統後,連鎖企業缺乏數據的情形已有所緩解,但決策需要的信息在數量、質量和時效上的標準都大大了。
提高結構分析是連鎖企業經常進行的數據分析工作,銷售結構分析是結構分析內容之一,在分析銷售數據時,不但需要知道銷售總量,同時也必須瞭解銷售結構。例如,一家經營150家門店的連鎖公司,商品a和商品b的日銷售數量都是1500,總量是相同的但商品a只有一家門店銷售,而商品b在153家門店都有銷售。而且每家門店的銷售量都是10,銷售存在非常大的差異。從平均數的角度看,商品a和商品b的店均日銷售數都是10,體現不出兩十商品銷售的差異。如果商品淘汰的數量指標是1500,則商品a和b都要被淘汰,但商品a只有一家門店銷售,單店銷售量高.從門店的角度看是不能淘汰的;而商品b單店銷售量低,從總部的角度和門店的角度都是可以淘汰的。這個例子雖然比較極端,但說明瞭銷售結構對商品決策的重要性。
獲取銷售結構信息最直觀的辦法是觀察比較每一門店的銷售數據還可以用頻度統計的方法,將銷售數據劃分為若幹區間,統計每一區間的門店數量,計算其頻度或用分類的方法,根據定義的標準,給商品分類如統計80%的銷售量對應的門店數量比例等,即所謂80—20分析:但上方法都有一個共同的缺點:總括性差,不得不用多個數值來反映結構以下我們借鑒經濟學中分析收人分配程度的思路,提出一種分析銷售結構的方法。
二、引入洛倫茲繫數
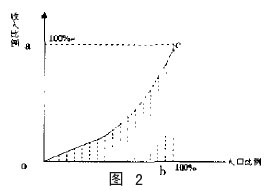
經濟學家在研究收人分配時,用洛倫茲曲線來比較不同國度的收入分配程度,如下圖。
將收人由低至高排序後,依次統計:1%的人口在總收人中的比例,2%的人口在總收人中的比例?一直至的人口在總收入中的比例。繪製成圖就得到曲線oc。
如圖上時,收人是最平均的,1%的人口的收入比例是1%,2%的人口的收入比例是2%,99%的人口的收入比例是99%,100%的人口的收入比例是100%
如上圖時,收人是最不平均的,99%的人口的收人比例是0%,100%的人口的收入比例是100%,即1%的人口占有了100%的收人。
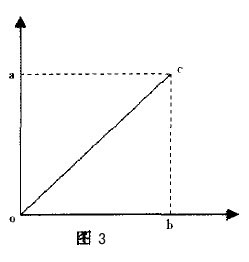
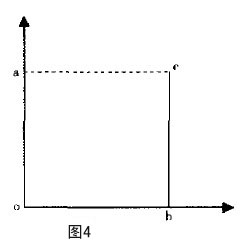
如果定義:洛倫茲繫數=oac的面積/oacb的面積(圖2),那麼,洛倫茲繫數反映了洛倫茲曲線的特征。圖3洛倫茲繫數=0.5,收人最平均;圖4的洛倫茲繫數=0,最不平均。
三、洛倫茲繫數銷售分析方法
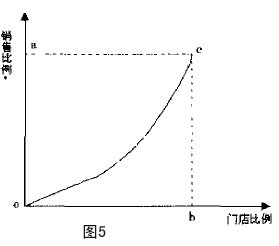
我們可以用洛倫茲繫數的原理來分析銷售,計算商品的洛倫茲繫數(見圖5)。取規定時段的幾店銷售數據,由低至高排序後,依次統計:1%的門店在總銷售中的比例,2%的門店在總銷售中的比例……直至99%的門店在總銷售中的比例,100%的九店在總銷售中的比例。實際運用時,門店的比例可根據具體情況處理,不必機械地照搬1%的間距。
當銷售洛倫茲繫數=0.5時,形狀如圖3時,銷售是最平均的。
當銷售洛倫茲繫數=0時,形狀如圖4時,銷售是最不平均的。99%的門店銷售額是0,100%的門店銷售是1O0%,即1%的門店創造了l00%的銷售額。清楚演算法後,具體計算可通過電腦程式實現。
四、運用
1.商品銷售洛倫茲繫數可以定量比較商品銷售的均勻程度,作為反映銷售結構(銷售分佈的指標。因此銷售洛倫茲繫數可作為一個管理控制的指標。
2.也可以計算門店銷售總額的洛倫茲繫數,將門店銷售總額捧序後,進行計算。同理可以計算毛利的洛倫茲繫數。其實,洛倫茲繫數可以在更廣泛的範圍內使用。
3.可以定義洛倫茲繫數比率,如門店商品的洛倫茲繫數/門店銷售總額的洛倫茲繫數,這個比率也可以更精確反映銷售的均勻程度。

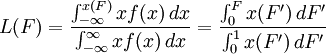








多謝!舉的例子很直觀,使我最終解開半月的迷惑,最終明白了橫軸的含義。