期望值法

出自 MBA智库百科(https://wiki.mbalib.com/)

期望值法（Expectancy Method）

　　期望值法是通過計算項目凈現值的期望值和凈現值大於或等於零時的累計概率，來比較方案優劣、確定項目可行性和風險程度的方法。

　　採用期望值法進行概率分析，一般需要遵循以下步驟：

　　1、選用凈現值作為分析對象，並分析選定與之有關的主要不確定性因素。

　　2、按照窮舉互斥原則，確定各不確定性因素可能發生的狀態或變化範圍。

　　3、分別估算各不確定性因素每種情況下發生的概率。各不確定性因素在每種情況下的概率，必須小於等於1、大於等於零，且所有可能發生情況的概率之和必須等於l。這裡的概率為主觀概率，是在充分掌握有關資料基礎之上，由專家學者依據其自己的知識、經驗經系統分析之後，主觀判斷作出的。

　　4、分別計算各可能發生情況下的凈現值(NPV)。各年凈現值期望值、整個項目壽命周期凈現值的期望值、各年凈現值期望值的計算公式為：

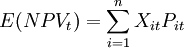
　　式中，E(NPV_t)為第t年凈現值期望值；X_it為第t年第i種情況下的凈現值；P_it為第t年第i種情況發生的概率，n為發生的狀態或變化範圍數。

　　整個項目壽命周期凈現值的期望值的計算公式為：

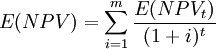
　　式中，E（NPV）為整個項目壽命周期凈現值的期望值；i為折舊率；M為項目壽命周期長度，E（NPVT）為第t年凈現值的期望值。

　　項目凈現值期望值大於零，則項目可行，否則，不可行。

　　5、計算各年凈現值標準差、整個項目壽命周期凈現值的標準差或標準差繫數，各年凈現值標準差的計算公式為：

　　式中，δ_t為第t年凈現值的標準差，其它符號意義同前。

　　整個項目壽命周期的標準差計算公式為：

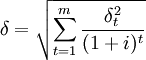
　　式中，δ為整個項目壽命周期的標準差。

　　凈現值標準差反映每年各種情況下凈現值的離散程度和整個項目壽命周期各年凈現值的離散程度，在一定的程度上，能夠說明項目風險的大小。但由於凈現值標準差的大小受凈現值期望值影響甚大，兩者基本上呈同方向變動。因此，單純以凈現值標準差大小衡量項目風險性高低，有時會得出不正確的結論。為此需要消除凈現值期望值大小的影響，利用下式計算整個項目壽命周期的標準差繫數：

　　式中，V為標準差繫數。一般地，V越小，項目的相對風險就越小，反之，項目的相對風險就越大。依據凈現值期望值、凈現值標準差和標準差繫數，可以用來選擇投資方案。判斷投資方案優劣的標準是：期望值相同、標準差小的方案為優；標準差相同、期望值大的方案為優；標準差繫數小的方案為優。

　　6、計算凈現值大於或等於零時的累計概率。累計概率值越大，項目所承擔的風險就越小。

　　7、對以上分析結果作綜合評價，說明項目是否可行及承擔風險性大小。

　　【例】某投資者以25萬元購買了一個商鋪單位2年的經營權，第一年凈現金流量可能為：22萬元、18萬元和14萬元，概率分別為0.2、0.6和o.2；第二年凈現金流量可能為：28萬元、22萬元和16萬元，概率分別為O.15、0.7和0.15，若折現率為10％，問該購買商鋪的投資是否可行。

　　【解】

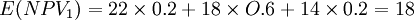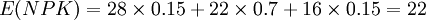　　(萬元)

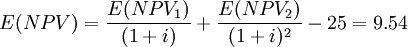　　(萬元)

　　(萬元)

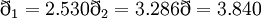
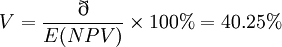
　　因此，該投資項目可行，且風險較小。

　　【例】某項目投資20萬元，建設期1年。據預測，經營期內的年收入可能為5、10、12.5萬元，相應的概率為0.3、O.5和0.2。同時，預計受技術進步的影響，經營期可能為2、3、4、5年，對應的可能性為0.2、0.2、0.5和0.1。如果折現率為10％，對凈現值作累計概率分析。

　　【解】以年收入為10萬元，經營期4年為例。該投資項目的凈現值為：

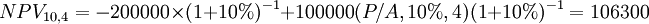　　 (元)。

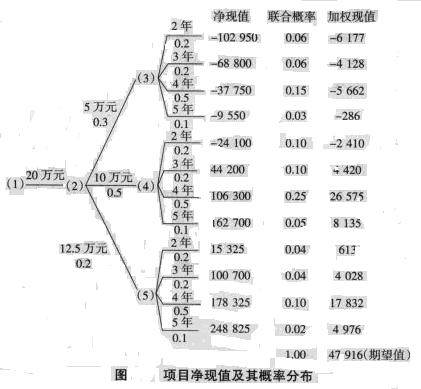
　　其他各種情況下的凈現值如圖所示。

　　可以計算得出，該投資項目的凈現值期望值為47916元，凈現值大於零的累計概率P(NPV>0)為0.6.表明該項目可行。