有效資產組合
出自 MBA智库百科(https://wiki.mbalib.com/)
有效資產組合(Efficient portfolio)
目錄 |
有效資產組合是指在一定的收益水平上承擔最小的風險或在一定的風險水平上獲得最大收益的資產組合.在幾何分析法中,有效資產組合集是由一系列臨界線導出來的。
有效資產組合選擇的幾何分析[1]
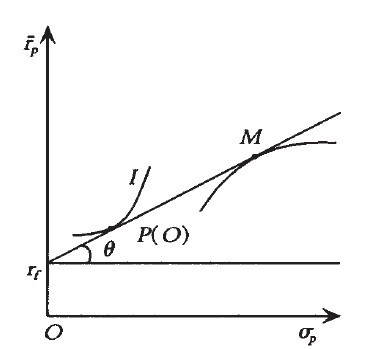
如圖(1)所示:橫坐標表示資產組合收益率的標準差δp,縱坐標表示資產組合的收益率 ;設無風險利率為rf,則根據文獻[2]可知:任何投資者的有效資產組合集為從點(O,rf)出發通過點M的一條射線.其中點M即為給定無風險利率rf下風險資產有效組合,所以無論投資者的收益-風險特征如何,他們所選擇的有效資產組合肯定是落在這條射線上:即由無風險資產和風險資產有效組合構成.至於不同投資者會選擇射線上的不同組合完全取決於其收益-風險偏好.投資者的收益-風險偏好可以用其無差異曲線表示.根據文獻[3]的描述可知無差異曲線是凸向橫軸!如圖(1)中的曲線I此時根據均值方差理論從投資者的不滿足性和風險厭惡性出發,可知投資者肯定會選擇其無差異曲線與線性有效集的切點,如圖(1)中的P點.並且可以判斷P點沿著射線離點(O,rf)越遠,表明投資者的越是風險愛好型的;反之,表明投資者的越是風險厭惡型的.
;設無風險利率為rf,則根據文獻[2]可知:任何投資者的有效資產組合集為從點(O,rf)出發通過點M的一條射線.其中點M即為給定無風險利率rf下風險資產有效組合,所以無論投資者的收益-風險特征如何,他們所選擇的有效資產組合肯定是落在這條射線上:即由無風險資產和風險資產有效組合構成.至於不同投資者會選擇射線上的不同組合完全取決於其收益-風險偏好.投資者的收益-風險偏好可以用其無差異曲線表示.根據文獻[3]的描述可知無差異曲線是凸向橫軸!如圖(1)中的曲線I此時根據均值方差理論從投資者的不滿足性和風險厭惡性出發,可知投資者肯定會選擇其無差異曲線與線性有效集的切點,如圖(1)中的P點.並且可以判斷P點沿著射線離點(O,rf)越遠,表明投資者的越是風險愛好型的;反之,表明投資者的越是風險厭惡型的.
有效資產組合的數學描述[1]
根據第一部分的定性分析,資者有效資產組合的選擇分三個步驟:
第一步尋求有效資產組合集;
第二步確定投資者的無差異曲線及其方程;
第三步根據投資者的不滿足性和風險厭惡性選擇有效資產組合,確定投資方案.
尋求有效資產組合集的實質即為從點(O,rf)出發的射線中與風險資產組合有效集相切的切點合集M的風險資產構成.根據圖(1)可知使得該射線與橫軸的夾角(設為δ)達到最大,所以此問題可歸結為(1)式表示的數學規劃問題.設市場上有N 種風險資產,此時無風險利率為rf,ri(i=1,2,3…N)表示第1種風險資產的收益率,δi(i=1,2,3…N)表示第1種風險資產的收益率的標準差,δij(i,j=1,2,3…N.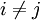 )
表示任兩種風險資產的收益率的協方差.由這N種風險資產構成的組合P的期望收益率
)
表示任兩種風險資產的收益率的協方差.由這N種風險資產構成的組合P的期望收益率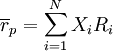 ,其標準差
,其標準差
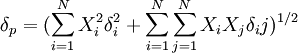 ,
,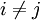 ,若滿足(1)式條件,則組合P為風險資產組合M,並求Xi,確定風險資產構成.
,若滿足(1)式條件,則組合P為風險資產組合M,並求Xi,確定風險資產構成.
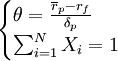 .(1)
.(1)
(1)式為約束極值問題,因為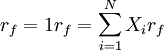 ,將其帶入目標函數消去約束方程,則(1)式變成無約束極值問題,如(2)式.
,將其帶入目標函數消去約束方程,則(1)式變成無約束極值問題,如(2)式.
 ,
,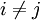 . (2)
. (2)
對於(2)式,為使θ最大,即要求
 (i=1,2,…,N),若設
(i=1,2,…,N),若設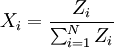 ,則參照文獻[2]
[2]給出的推導,整理並簡化得如下方程組(3):
,則參照文獻[2]
[2]給出的推導,整理並簡化得如下方程組(3):
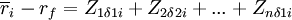 (i=1,2,3...,N) . (3)
(i=1,2,3...,N) . (3)
方程組(3)有N個方程,N個未知數Zi(1,2,3...,N).因為rf,δNi 已知,Zi(1,2,3...,N)的解是確定的,從而Xi
的解也是確定的,所以風險資產有效組合M隨之確定.此時,可求出\overline{r}_M,\delta_M,確定有效資產組合集,其為從點(O,rf)出發斜率為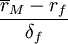 的射線,該射線即為資本市場線,其方程為:
的射線,該射線即為資本市場線,其方程為:
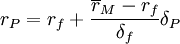 . (4)
. (4)
投資者的無差異曲線反映了投資者對收益-風險組合的同樣滿足程度參考文獻[3][3]關於風險容忍度的討論,設投資者的投資收益率和風險分別表示為r和δ2,則其無差異曲線方程可表示為
r = a + bδ2. (5)
其中a,b為已知常數,所以投資者的無差異曲線如圖(1)所示的I.
對於理性投資者,可以確定其資產組合肯定同時落在有效資產組合集和無差異曲線上,若設投資者資產組合的收益率為r0,收益率的標準差為
δo,則其滿足(4)式和(5)式,即
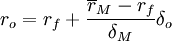 . (6)
. (6)
 . (7)
. (7)
根據投資者的不滿足性和風險厭惡性特征,投資者的資產組合集O若為有效資產組合,則O點一定是(7)式表示的曲線與(6)式表示的射線唯一的相切點.根據切點含義,在O點處由(6)式和(7)式表示的曲線斜率相等,即
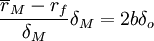 . (8)
. (8)
根據有效資產組合集的性質,投資者的有效資產組合O是由無風險資產和有效風險資產組合M構成,若設投資有效風險資產組合的資金比例為W,則投資無風險資產的比例為1-W,所以
δO = WδM ,將其代入(8)式得
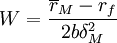 . (9)
. (9)
由(9)式確定W,就可以確定該投資者有效資產組合的構成,即無風險資產的資金比例為1-W,任一風險資產的資金比例為WXi,(i=1,2,...,N),所以特定投資者就可以按上述投資比例確定其有效資產組合.