多目標決策法
出自 MBA智库百科(https://wiki.mbalib.com/)
多目標決策法(Multi-objective decision-making method)
目錄 |
多目標決策是對多個相互矛盾的目標進行科學、合理的選優,然後作出決策的理論和方法。它是20世紀70年代後迅速發展起來的管理科學的一個新的分支。多目標決策與只為了達到一個目標而從許多可行方案中選出最佳方案的一般決策有所不同。
多目標決策有各種各樣的形式,但其基本特征有兩點,這就是目標間的不可公度性和目標間的矛盾性。前者是指各目標間通常沒有統一的度量標準,因而難於進行比較後者是指增加某一目標的利益,常常使另外的某-或某些目標變壞,因而通常不存在一般意義下的最優解。顯然,多目標決策與單目標決策有著質的區別。[1]
從人們在多目標條件下合理進行決策的過程和機制從上分析,多目標決策的理論主要有:多目標決策過程的分析和描述;衝突性的分解和理想點轉移的理論;多屬性效用理論;需求的多重性和層次性理論等。它們是構成多目標決策分析方法的理論基礎。
在多目標決策中,有一部分方案經比較後可以淘汰,稱為劣解;但還有一批方案既不能淘汰,又不能互相比較,從多目標上考慮又都不是最優解,稱為“非劣解”(或“有效解”、“帕累托解)。
在社會經濟系統的研究控制過程中我們所面臨的系統決策問題常常是多目標的,例如我們在研究生產過程的組織決策時,既要考慮生產系統的產量最大,又要使產品質量高,生產成本低等。這些目標之間相互作用和矛盾,使決策過程相當複雜使決策者常常很難輕易作出決策。這類具有多個目標的決策總是就是多目標決策。多目標決策方法現已廣泛地應用於工藝過程、工藝設計、配方配比、水資源利用、環境、人口、教育、能源、企業高速武器系統設計和評價、經濟管理等領域。在多目標決策實踐中也應遵循一定的行為準則,主要包括:
(1)在滿足決策需要的前提下,儘量減少目標個數。可採用剔除從屬性目標,並把類似的目標合併為一個目標,或者把那些只要求達到起碼標準而不要求達到最優的次要目標降為約束條件;以及通過同度量求和、求平均值或構成綜合函數的方法,用綜合指標來代替單項指標的辦法達到目的。
(2)按照目標的輕重緩急,決定目標的取捨。為此,就要將目標按重要程度排列出一個順序,並規定出重要性繫數,以便在選優決策時有所遵循。
(3)對相互矛盾的目標,應以總目標為基準進行協調,力求對各目標全面考慮,統籌兼顧。
處理多目標決策問題,第一步就是找出非劣解,如果非劣解只有一個,就薛蹭為最優方案,如果不只一個,就無最優解,而需按一定法則從它們之中選出一個比較好的作為答案,這個解稱為“較好解”。
這些概念用數學語言來描述,可以表示為:有 N個目標 ![f_1(X_i),f_2(X_i),f_3(X_i),\ldots,f_n(X_i)(X=[X_1,X_2,\ldots X_m])](/w/images/math/c/6/b/c6b41cffa7ebfbb79ce1783409c92d70.png) ,X是各函數中的變數,決策的目的是使各目標均取極大值,即
,X是各函數中的變數,決策的目的是使各目標均取極大值,即
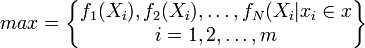 (x是 xi的集合)
(x是 xi的集合)
所謂這一問題的非劣解 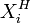 ,是指我們再也找不到一個或一組 Xi值,使得對所有的fi(Xi)[j=1,2,…N]來說,都有
,是指我們再也找不到一個或一組 Xi值,使得對所有的fi(Xi)[j=1,2,…N]來說,都有
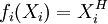
既然找不到一個或一組 Xi值能使
 ,則
,則 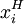 就是非劣解
就是非劣解
或
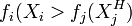
若另有一組 Xi值,使 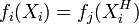 ,則這組 xi值亦為非劣解。
,則這組 xi值亦為非劣解。
這後一個條件是為了防止有兩個目標值完全相同的非劣解時,將其中一個錯判為劣解。
多目標決策的方法很多,有的要用線性規劃、非線性規劃、目標規劃等方法。這裡只介紹一下多目標決策中方案有限的幾種方法。對於多目標的方案有限的決策問題一般先採用列表的方式。
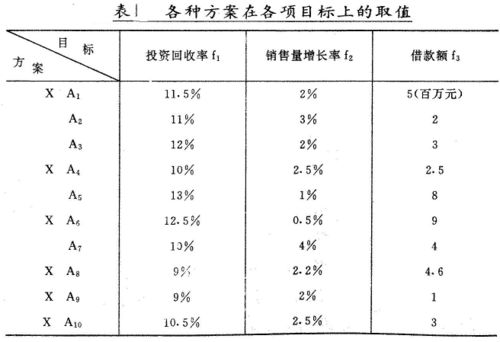
例,某廠要擴大生產,有 10個可行方案。考察各方案優劣的目標有投資回收率 f1,(越大越好),銷售量的增長率f2(越大越好),借款額 f3(越低越好)。各種方案在各項目標上的取值情況見表1,要求找出非劣解,並從中選出一個“較好解”。
顯然,從表中經過比較即可淘汰劣解,我們在劣解方案的在側打上一個“X”號,例如 A1被 A3淘汰,A6被 A5淘汰等等,最後留下A2,A3,A5,A7,A9為非劣解。下一步從中選出“較好解”。
常用的方法有下述幾種;
1.化多為少法。即將多目標改為由一個統一的綜合目標來比較方案。包括綜合評分法、平方和法及約束法。
2.目標分層法。把所有目標分別按其重要性排一個次序。
3.分層序列法:將所有目標按其重要性程度依次排序,先求出第一個最重要的目標的最優解,然後在保證前一目標最優解的前提下依次求下一目標的最優解,一直求到最後一個目標為止。
4.直接求非劣解法:先求出一組非劣解,然後按事先確定好的評價標準從中找出一個滿意的解。
5.目標規劃法:對於每一個目標都事先給定一個期望值,然後在滿足系統一定約束條件下,找出與目標期望值最近的解。
6.多屬性效用法:各個目標均用表示效用程度大小的效用函數表示,通過效用函數構成多目標的綜合效用函數,以此來評價各個可行方案的優劣。
7.層次分析法:把目標體繫結構予以展開,求得目標與決策方案的計量關係。
8.重排序法:把原來的不好比較的非劣解通過其他辦法使其排出優劣次序來。
- ↑ 楊劍波. 多目標決策方法與應用[M]. 湖南出版社, 1996.








線性加權法、TOPSIS法和密切值法??