全球专业中文经管百科，由121,994位网友共同编写而成，共计436,017个条目

查看

工具▼

預測波動率

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

目錄

1 什麼是預測波動率
2 預測波動率的度量方法

什麼是預測波動率

　　預測波動率又稱為預期波動率，它是指運用統計推斷方法對實際波動率進行預測得到的結果，並將其用於期權定價模型，確定出期權的理論價值。因此，預測波動率是人們對期權進行理論定價時實際使用的波動率。這就是說，在討論期權定價問題時所用的波動率一般均是指預測波動率。需要說明的是，預測波動率並不等於歷史波動率，因為前者是人們對實際波動率的理解和認識，當然，歷史波動率往往是這種理論和認識的基礎。除此之外，人們對實際波動率的預測還可能來自經驗判斷等其他方面。

預測波動率的度量方法

　　（一）移動平均法

　　移動平均法是指以過去N天的收益率的方差作為當日波動率的估計值，分為簡單移動平均和加權移動平均兩種方法。簡單移動平均法將每天的收益率看成是等權重的，加權移動平均法則對不同時點賦予不同的權重。

　　簡單移動平均法：

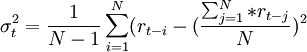
　　 $\sigma_{t}^2=\frac{1}{N-1}\sum_{i=1}^N (r_{t-i}-(\frac{\sum_{j=1}^N*r_{t-j}}{N})^2$

　　加權移動平均法：

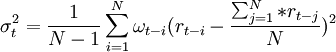
　　 $\sigma_t^2=\frac{1}{N-1}\sum_{i=1}^N\omega_{t-i} (r_{t-i}-\frac{\sum_{j=1}^N*r_{t-j}}{N})^2$

　　其中， $r t - i$ 為t-i時刻的收益率， $ω t - i$ 為t-i時刻的權重。

　　（二）指數平滑法

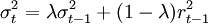
　　 $\sigma_{t}^2=\lambda\sigma_{t-1}^2+(1-\lambda)r_{t-1}^2$

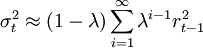
　　 $\sigma_{t}^2\approx(1-\lambda)\sum_{i=1}^\infty\lambda^{i-1}r_{t-1}^2$

　　其中， $λ$ 為衰退因數，即平滑繫數，0< $λ$ <1。

　　將指數平滑公式通過遞推推導，可以得到t時刻的波動率 $σ$ 與收益率r之間的關係式。運用此方法，需要確定參數 $λ$ 。

　　（三）GARCH模型法

　　藉助Garch模型，可以估計和預測波動率。

　　Bollerslev於1986年對自回歸條件異方差模型（ARCH）進行了推廣，提出了廣義自回歸條件異方差模型（GARCH）。標準的Garch(q,p)模型為：

　　 $y t = X t Υ + μ$

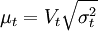
　　 $\mu_t=V_t\sqrt{\sigma_t^2}$

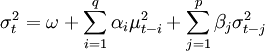
　　 $\sigma_t^2=\omega+\sum_{i=1}^q\alpha_i\mu_{t-i}^2+\sum_{j=1}^p\beta_j\sigma_{t-j}^2$

　　其中，p是GARCH項的次數，q是ARCH項的次數, $σ$ 是條件方差。

　　此外，還有隨機波動模型（SV）以及其擴展模型、自回歸移動平均模型（ARIMA/ARFIMA）等，用於對金融資產波動率的估計。另外，也可以通過模型預計隱含波動率。

取自"https://wiki.mbalib.com/zh-tw/%E9%A2%84%E6%B5%8B%E6%B3%A2%E5%8A%A8%E7%8E%87"

打开MBA智库App, 阅读完整内容打开App

如果您認為本條目還有待完善，需要補充新內容或修改錯誤內容，請編輯條目或投訴舉報。

本条目由以下用户参与贡献

頁面分類: 證券術語

評論(共0條)

提示:評論內容為網友針對條目"預測波動率"展開的討論，與本站觀點立場無關。

發表評論請文明上網，理性發言並遵守有關規定。

以上内容根据网友推荐自动排序生成

闽公网安备 35020302032707号