歷史波動率

出自 MBA智库百科(https://wiki.mbalib.com/)

歷史波動率(History Volatility,HV)

　　歷史波動率是基於過去的統計分析得出的，假定未來是過去的延伸，利用歷史方法估計波動率類似於估計標的資產收益系列的標準差。

　　在股票市場中，歷史波動率反映標的股價過去的波動。然而，由於股價波動難以預測，利用歷史波動率對權證價格進行預測一般都不能保證準確，但是由於目前我國內地沒有權證市場，因而無法獲得權證價格，也就無法計算隱含波動率。因此權證發行商與投資者在權證發行初期只能利用歷史波動率作參考。

　　下麵以計算股票的歷史波動率為例加以說明。

　　1、從市場上獲得標的股票在固定時間間隔(如每天、每周或每月等)上的價格。

　　2、對於每個時間段，求出該時間段末的股價與該時段初的股價之比的自然對數。

　　3、求出這些對數值的標準差，再乘以一年中包含的時段數量的平方根(如，選取時間間隔為每天，則若扣除閉市，每年中有250個交易日，應乘以根號250)，得到的即為歷史波動率。

　　方法一：百分比價格變動法(即價格的環比增長速度)。

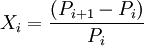　　　　(1)

　　(1)式中，X_i是資產的百分比收益，P_i是昨天(基期)資產的價格，P_{i + 1}是今天(報告期)資產的價格。

　　方法二：對數價格變動法。

　　　　(2)

　　(2)式中，X_i是資產的對數收益，P_i是昨天(基期)資產的價格，P_{i + 1}是今天(報告期)資產的價格。

　　值得註意的是，上述兩個公式的假定不一樣，百分比收益公式假定有固定的不連續間隔價格變化，而對數收益公式假定價格是連續的變化。在Black-Scholes模型中，假定價格變動是連續的，可從連續利率因數e ^{− RT}將敲定價格換算成現值這一事實推導得出。所以，對於這個模型，對數收益公式是確定波動率的合適公式。針對資產的對數收益求其平均數，然後根據下麵公式得到歷史波動率的估計值。

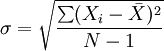
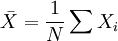
　　這裡，N是觀察值的數量， σ代表對數收益的平均離差，即標準差。若將日、周等標準差轉化為年標準差，需要乘以以年為單位的頻數長度的平方根。如歐洲期權市場一年有252個工作日，X_i為日變數，則年波動率為為。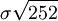

　　歷史波動率估計應考慮的問題：

　　1、歷史波動率估計的數據頻率

　　估計歷史波動率可使用的數據頻率有：交易日、日曆日、星期、月份或季度。選擇不同的數據頻率，波動率的結果是不一樣的。如果取得的系列數據不理想，結果會造成較大的估計錯誤。要使統計誤差最小，大部分的分析家儘可能利用更小單位的每日數據。但選擇日變數，面臨對日曆天數、交易日(工作日)、經濟日的選擇。日曆天數是已過去的波動率估計日的實際值，交易日等於日曆天數減去周末和節假日，經濟日指一些影響資產價格變動的重要事件發生時波動率高的日子。首要的事情是，在估計標的資產波動率時，我們應該選用日曆日還是交易日?很清楚的是當沒有人買人和賣出期權時，期權價格將永遠不會發生變化，因而，由於市場和交易引起波動率變化而導致價格發生變化。所以．在進行歷史波動率估計時，應當僅僅利用交易日觀察值。

　　2、歷史波動率經濟日對預期波動率的影響

　　估計歷史波動率的目的是預測未來波動率的水平。通過對過去數據的觀察，發現在整個有效期內的波動率是不一樣的，這就是異方差性問題。分析家預測未來波動率時，必須基於過去的歷史波動率估計中“經濟日”的數值，猜測一個更為準確的概率預測樣本期的經濟日和正常日天數，這樣，才能得出將在整個時期發生的實際波動率的預期。隨著時間的推移，每天計算波動率預期時，都要考慮過去的經濟日和正常日。預期的“經濟日”越多，估計未來波動率越高，“經濟日”越少，預期波動率越低。所以，波動率預期必須考慮計量正常交易日和經濟交易日的差異。

　　例如，擁有1993年5月25日至1994年5月4日的義大利政府債券合約期貨(BTP)的日波動率，歷史分析期間總觀察值240日，第一步，將日波動率從低到高排序，假定出現高波動率的概率為25％，在第180個觀察值之下的結果是正常日，在第180以上的60個觀察值被分在經濟日里。第二步，用簡單算術平均法分別計算經濟日和正常日發生的平均波動率，經濟日平均波動率高達1 6.326％，正常日平均波動率是4.077％。第三步，用加權算術平均法預測5月5日至5月20日到期日的BTP期貨合約的波動率預期。隨著時間的推移，至到期日那一天，每日的預期波動率=(正常日天數×正常 波動率+經濟日天數×經濟波動率)÷(正常日天數+經濟日天數)。在此，首先運用波動率守恆定律，按照歷史波動率估計中經濟日出現的概率預測未來12個工作日出現的經濟日和正常日的天數。顯然，經濟日占1/4，有3日；正常日占3/4，有9日。

　　BTP期貨波動率預期例子：

　　數據：1994年5月4日到1994年5月20日的波動率預期。

　　(9x4.077％+3x16.326％)／12=7.1393％

　　3、估計的樣本期間的選擇

　　抽樣技術表明，增加估計期樣本數量，可以減少預測的標準誤差，但並不能一味地增加樣本數量，因為預測明天的波動率，使用最近幾天的數值反而比過去五年的數值更有效。分析家們在估計歷史波動率時有三種選擇，其一是採用更長期間的波動率，利用過去一年的交易日；其二是採用更短的樣本期，如3O天或90天交易日；其三是採用過去期間等於要預測的將來時長。如果所有三個樣本期和合成波動率(正常日和經濟日的波動率合成)幾乎是一樣的，則可以認定，這一資產在整個時期的波動率可能是穩定的。但利用三個樣本期計算的結果總是有差異，則可利用基於更常用的數據期間，或與整個預測期相當的期間進行計算；或根據研究需要，對長期、中期和短期波動率賦予一定的權數(如1/2，1/3或1/4等)進行加權平均得到合成波動率。

　　4、估計波動率的價格選擇

　　標的資產的價格有：開盤價、收盤價、最高價、最低價，理論上對歷史波動率估計的價格作了各種研究，大部分情況下，歷史波動率估計中使用的價格是每日市場的收盤價，但外匯市場沒有收盤價，則有學者利用最高價／最低價來計量波動率。無論採用什麼價格，歷史波動率估計和實際波動率一致時，才能證明這一估計是好的。

　　在測算的波動率時，歷史波動率是使用過去的股價數據計算的波動率數值，而隱含波動率是將市場上的權證交易價格代入權證理論價格模型，反推出來的波動率數值。

　　隱含波動率受市場買賣力量的影響，與歷史波動率未必相同。某一月份期貨只有一個歷史波動率，但其隱含波動率卻很多。不同執行價格的看漲期權、看跌期權的隱含波動率都不盡相同。實際交易中，隱含波動率更受交易者的重視。

　　運用期權定價模型計算期權理論價格需要五個參數，其他四個參數都可以方便得到，只有波動率是未知的。從這個角度講，做期權就是做預期的波動率。而歷史波動率和隱含波動率可以用來幫助交易者來預測未來的波動率。