異方差性
出自 MBA智库百科(https://wiki.mbalib.com/)
異方差性（heteroscedasticity）
目錄 |
異方差性的定義[1]
設線性回歸模型為:
經典回歸中所謂同方差是指不同隨機誤差項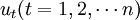
的方差相同，即：
var(ut) = σ2
如果隨機誤差項的方差不是常數，則稱隨機項 具有異方差性（heteroskedasticity），即:
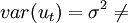常數u_t(t=1,2,\cdots n)
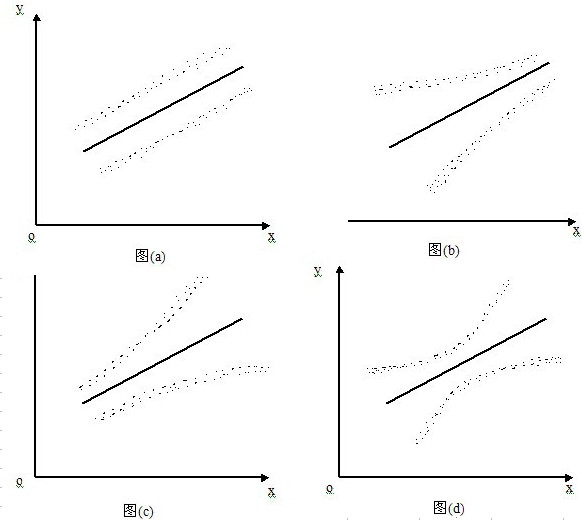
異方差性的幾何直觀表示形式，可藉助觀測值的散佈圖表示。以一元線性回歸為例，在散佈圖上，就是樣本殘差平方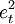
隨解釋變數的變化而變化。
產生異方差性的原因[2]
在計量經濟研究中，異方差性的產生原因主要有以下幾種。
- 1.模型中遺漏了某些解釋變數
如果模型中只包含所要研究的幾個主要因素，其他被省略的因素對被解釋變數的影響都歸入了隨機誤差項，則可能使隨機誤差項產生異方差性。
例如，用截面數據研究消費函數，根據絕對收入消費原理，設消費函數為：
yt = b0 + b1x1 + ut
其中：yt為家庭消費支出，xt為家庭可支配收入。在該模型中，物價水平Pt沒有包括在解釋變數中，但它對消費支出是有影響的，該影響因素卻被放在隨機誤差項中。如果物價水平是影響消費的重要部分，則很可能使隨機誤差的方差變動呈現異方差性。另一方面如果用xt / Pt只表示不同家庭收入組的數據來研究消費函數，則不同收入組在消費支出上的差異是不同的。高收入組的消費支出差異應該很大，而低收入組的消費支出差異就很小。不同收入的家庭其消費支出有不同的差異變化。
再例如，用截面數據研究某一時點上不同地區的某類企業的生產函數，其模型為：
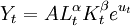
u為隨機誤差項，它包含了除資本K和勞動力L以外的其他因素對產出Y的影響，比如不同企業在設計上、生產工藝上的區別，技術熟練程度或管理上的差別以及其他因素，這些因素在小企業之間差別不大，而在大企業之間則相差很遠，隨機誤差項隨L、K增大而增大。由於不同的地區這些因素不同造成了對產出的影響出現差異，使得模型中的u具有異方差性，並且這種異方差性的表現是隨資本和勞動力的增加而有規律變化的。
- 2.模型函數形式的設定誤差
在一般情況下，解釋變數與被解釋變數之間的關係是比較複雜的非線性關係。在構造模型時，為了簡化模型，用線性模型代替了非線性關係，或者用簡單的非線性模型代替了複雜的非線性關係，造成了模型關係不准確的誤差。如將指數曲線模型誤設成了線性模型，則誤差有增大的趨勢。
- 3.樣本數據的測量誤差
一方面，樣本數據的測量誤差常隨時間的推移而逐步積累，從而會引起隨機誤差項的方差增加。另一方面，隨著時間的推移，抽樣技術和其他收集資料方法的改進，也使得樣本的測量誤差逐步減少，從而引起隨機誤差的方差減小。因此，在時間序列資料中，由於在不同時期測量誤差的大小不同，從而隨機項就不具有同方差性。
- 4.隨機因素的影響
經濟變數本身受很多隨機因素影響(比如政策變動、自然災害或金融危機等)，不具有確定性和重覆性，同時，社會經濟問題涉及人的思維和行為，也涉及各階層的物質利益，人的行為具有很多不確定因素。
因此，經濟分析中經常會遇到異方差性的問題。而且經驗表明，利用橫截面數據建立模型時，由於在不同樣本點上(解釋變數之外)其他因素影響的差異較大，所以比時間序列資料更容易產生異方差性。
在實際經濟計量分析中，絕對嚴格的同方差性幾乎是不可能的，異方差性可以說是一種普遍的現象。
異方差性的影響[1]
- 1.對模型參數估計值無偏性的影響
以一元線性回歸模型為例。設一元線性回歸模型為yt = b0 + b1xt + ut，隨機誤差項ut的方差隨解釋變數的變化而變化：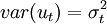
，其他條件不變。此時：
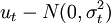。在高斯——馬爾可夫定理證明過程中曾經得到：
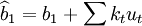，因此，
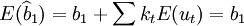。這表明b1滿足無偏性。同理可以證明
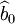也是b0的無偏估計量。
由此可見，隨機誤差項存在異方差性，並不影響模型參數最小二乘估計值的無偏性。
- 2.對模型參數估計值有效性的影響
在上述假定下參數b1的估計值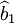
的方差為
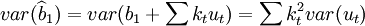
在隨機誤差項ut同方差的假定下，則參數的估計值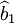的方差為
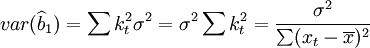
在隨機誤差項ut存在異方差條件下，假設參數估計值為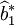
，=var（ut=1,2,…n）,此時，
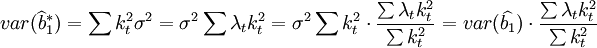
比較上式兩端，當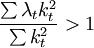
時，有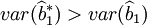
從而說明在隨機誤差項ut存在異方差條件下，最小二乘估計量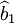不再具有最小方差。同理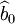也有類似的結果。
由此可見，當線性回歸模型的隨機誤差項存在異方差時，參數的最小二乘估計量不是一個有效的估計量。
- 3.對模型參數估計值顯著性檢驗的影響
在同方差的情況下，如果以σ2的無偏估計量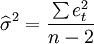
估計σ2，就可以得到繫數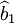的標準誤差為
但是，在異方差的情況下，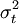
是一些不同的數值，只有估計出每一個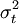之後才能得到繫數的標準誤差，這在只有一組樣本觀測值的情況下是無法做到的。而且如果設
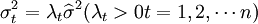，則在異方差的情況下，繫數的標準誤差：
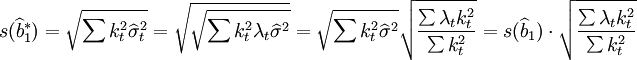
因此，如果仍然用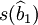
計算繫數的標準誤差，將會產生估計偏差，偏差的大小取決於第二個因數值
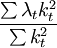的大小，當其大於1時，則會過低估計繫數的誤差；反之，則做出了過高的估計。因而，檢驗的可靠性降低。
在異方差情況下，無法正確估計繫數的標準誤差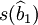，用t統計量為
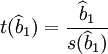來判斷解釋變數影響的顯著性將失去意義。
評論(共3條)
2中第三個式子里分母下是不是少了個求和符號？
謝您的指正，現已更改，MBA智庫百科是可以自由修改編輯的，您也可以直接參与！
在用線性回歸解決計量經濟學問題的時候，如果異方差性是無條件異方差性（unconditional heteroskedasticity），其實是可以認為RSS和估計值b的方差是準確的，檢驗也是可靠的。需要修正的異方差性是有條件異方差性（conditional heteroskedasticity）。如果用布倫斯-帕甘（Breusch–Pagan）檢驗或者懷特（White）檢驗推得有條件異方差性存在，現代統計學軟體都有重新計算RSS和估計值b的方差的功能，叫做heteroskedasticity-adjusted output。重新計算這兩個以後，檢驗的可靠性就恢復了。
2中第三個式子里分母下是不是少了個求和符號？