异方差性
出自 MBA智库百科(https://wiki.mbalib.com/)
异方差性（heteroscedasticity）
目录 |
异方差性的定义[1]
设线性回归模型为:
经典回归中所谓同方差是指不同随机误差项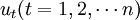
的方差相同，即：
var(ut) = σ2
如果随机误差项的方差不是常数，则称随机项 具有异方差性（heteroskedasticity），即:
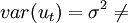常数u_t(t=1,2,\cdots n)
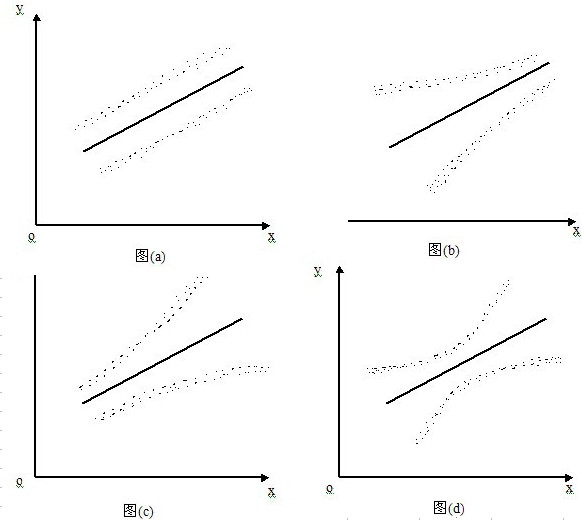
异方差性的几何直观表示形式，可借助观测值的散布图表示。以一元线性回归为例，在散布图上，就是样本残差平方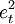
随解释变量的变化而变化。
产生异方差性的原因[2]
在计量经济研究中，异方差性的产生原因主要有以下几种。
- 1.模型中遗漏了某些解释变量
如果模型中只包含所要研究的几个主要因素，其他被省略的因素对被解释变量的影响都归入了随机误差项，则可能使随机误差项产生异方差性。
例如，用截面数据研究消费函数，根据绝对收入消费原理，设消费函数为：
yt = b0 + b1x1 + ut
其中：yt为家庭消费支出，xt为家庭可支配收入。在该模型中，物价水平Pt没有包括在解释变量中，但它对消费支出是有影响的，该影响因素却被放在随机误差项中。如果物价水平是影响消费的重要部分，则很可能使随机误差的方差变动呈现异方差性。另一方面如果用xt / Pt只表示不同家庭收入组的数据来研究消费函数，则不同收入组在消费支出上的差异是不同的。高收入组的消费支出差异应该很大，而低收入组的消费支出差异就很小。不同收入的家庭其消费支出有不同的差异变化。
再例如，用截面数据研究某一时点上不同地区的某类企业的生产函数，其模型为：
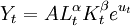
u为随机误差项，它包含了除资本K和劳动力L以外的其他因素对产出Y的影响，比如不同企业在设计上、生产工艺上的区别，技术熟练程度或管理上的差别以及其他因素，这些因素在小企业之间差别不大，而在大企业之间则相差很远，随机误差项随L、K增大而增大。由于不同的地区这些因素不同造成了对产出的影响出现差异，使得模型中的u具有异方差性，并且这种异方差性的表现是随资本和劳动力的增加而有规律变化的。
- 2.模型函数形式的设定误差
在一般情况下，解释变量与被解释变量之间的关系是比较复杂的非线性关系。在构造模型时，为了简化模型，用线性模型代替了非线性关系，或者用简单的非线性模型代替了复杂的非线性关系，造成了模型关系不准确的误差。如将指数曲线模型误设成了线性模型，则误差有增大的趋势。
- 3.样本数据的测量误差
一方面，样本数据的测量误差常随时间的推移而逐步积累，从而会引起随机误差项的方差增加。另一方面，随着时间的推移，抽样技术和其他收集资料方法的改进，也使得样本的测量误差逐步减少，从而引起随机误差的方差减小。因此，在时间序列资料中，由于在不同时期测量误差的大小不同，从而随机项就不具有同方差性。
- 4.随机因素的影响
经济变量本身受很多随机因素影响(比如政策变动、自然灾害或金融危机等)，不具有确定性和重复性，同时，社会经济问题涉及人的思维和行为，也涉及各阶层的物质利益，人的行为具有很多不确定因素。
因此，经济分析中经常会遇到异方差性的问题。而且经验表明，利用横截面数据建立模型时，由于在不同样本点上(解释变量之外)其他因素影响的差异较大，所以比时间序列资料更容易产生异方差性。
在实际经济计量分析中，绝对严格的同方差性几乎是不可能的，异方差性可以说是一种普遍的现象。
异方差性的影响[1]
- 1.对模型参数估计值无偏性的影响
以一元线性回归模型为例。设一元线性回归模型为yt = b0 + b1xt + ut，随机误差项ut的方差随解释变量的变化而变化：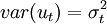
，其他条件不变。此时：
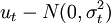。在高斯——马尔可夫定理证明过程中曾经得到：
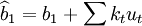，因此，
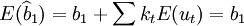。这表明b1满足无偏性。同理可以证明
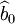也是b0的无偏估计量。
由此可见，随机误差项存在异方差性，并不影响模型参数最小二乘估计值的无偏性。
- 2.对模型参数估计值有效性的影响
在上述假定下参数b1的估计值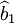
的方差为
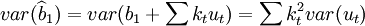
在随机误差项ut同方差的假定下，则参数的估计值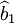的方差为
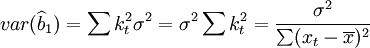
在随机误差项ut存在异方差条件下，假设参数估计值为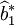
，=var（ut=1,2,…n）,此时，
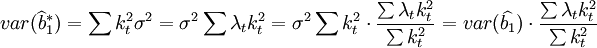
比较上式两端，当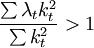
时，有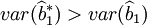
从而说明在随机误差项ut存在异方差条件下，最小二乘估计量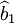不再具有最小方差。同理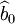也有类似的结果。
由此可见，当线性回归模型的随机误差项存在异方差时，参数的最小二乘估计量不是一个有效的估计量。
- 3.对模型参数估计值显著性检验的影响
在同方差的情况下，如果以σ2的无偏估计量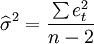
估计σ2，就可以得到系数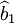的标准误差为
但是，在异方差的情况下，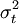
是一些不同的数值，只有估计出每一个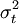之后才能得到系数的标准误差，这在只有一组样本观测值的情况下是无法做到的。而且如果设
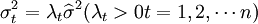，则在异方差的情况下，系数的标准误差：
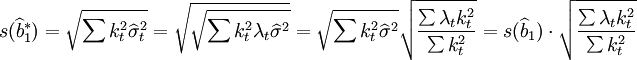
因此，如果仍然用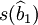
计算系数的标准误差，将会产生估计偏差，偏差的大小取决于第二个因子值
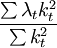的大小，当其大于1时，则会过低估计系数的误差；反之，则做出了过高的估计。因而，检验的可靠性降低。
在异方差情况下，无法正确估计系数的标准误差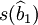，用t统计量为
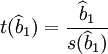来判断解释变量影响的显著性将失去意义。
评论(共3条)
2中第三个式子里分母下是不是少了个求和符号？
谢您的指正，现已更改，MBA智库百科是可以自由修改编辑的，您也可以直接参与！
在用线性回归解决计量经济学问题的时候，如果异方差性是无条件异方差性（unconditional heteroskedasticity），其实是可以认为RSS和估计值b的方差是准确的，检验也是可靠的。需要修正的异方差性是有条件异方差性（conditional heteroskedasticity）。如果用布伦斯-帕甘（Breusch–Pagan）检验或者怀特（White）检验推得有条件异方差性存在，现代统计学软件都有重新计算RSS和估计值b的方差的功能，叫做heteroskedasticity-adjusted output。重新计算这两个以后，检验的可靠性就恢复了。
2中第三个式子里分母下是不是少了个求和符号？