ARCH模型
出自 MBA智库百科(https://wiki.mbalib.com/)
ARCH模型(Autoregressive conditional heteroskedasticity model)
目錄 |
ARCH模型由美國加州大學聖迭哥分校羅伯特·恩格爾(Engle)教授1982年在《計量經濟學》雜誌(Econometrica)的一篇論文中首次提出。此後在計量經濟領域中得到迅速發展。
所謂ARCH模型,按照英文直譯是自回歸條件異方差模型。粗略地說,該模型將當前一切 可利用信息作為條件,並採用某種自回歸形式來刻劃方差的變異,對於一個時間序列而言,在不同時刻可利用的信息不同,而相應的條件方差也不同,利用ARCH 模型,可以刻划出隨時間而變異的條件方差。
作為一種全新的理論,ARCH模型在近十幾年裡取得了極為迅速的發展,已被廣泛地用於驗證金融理論中的規律描述以及金融市場的預測和決策。
ARCH模型是獲得2003年諾貝爾經濟學獎的計量經濟學成果之一。被認為是最集中反映了方差變化特點而被廣泛應用於金融數據時間序列分析的模型。ARCH模型是過去20年內金融計量學發展中最重大的創新。目前所有的波動率模型中,ARCH類模型無論從理論研究的深度還是從實證運用的廣泛性來說都是獨一無二的。
ARCH(q)模型:
均值方程:yt = Xβ + εt
εt的無條件方差是常數,但是其條件分佈為
εt|Ψt − 1~N(O,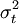 )
)
條件方差方程: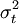 =
=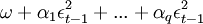
其中Ψt − 1是信息集
常數ω
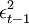 :滯後的殘差平方
:滯後的殘差平方
ARCH模型的基本思想是指在以前信息集下,某一時刻一個雜訊的發生是服從正態分佈。該正態分佈的均值為零,方差是一個隨時間變化的量(即為條件異方差)。並且這個隨時間變化的方差是過去有限項雜訊值平方的線性組合(即為自回歸)。這樣就構成了自回歸條件異方差模型。
由於需要使用到條件方差,我們這裡不採用恩格爾的比較嚴謹的複雜的數學表達式,而是採取下麵的表達方式,以便於我們把握模型的精髓。見如下數學表達:
Yt = βXt+εt (1)其中,
- Yt為被解釋變數,
- Xt為解釋變數,
- εt為誤差項。
如果誤差項的平方服從AR(q)過程,即εt2 =a0+a1εt-12 +a2εt-22 + …… + aqεt-q2 +ηt t =1,2,3…… (2)其中,
ηt獨立同分佈,並滿足E(ηt)= 0, D(ηt)= λ2 ,則稱上述模型是自回歸條件異方差模型。簡記為ARCH模型。稱序列εt 服從q階的ARCH的過程,記作εt -ARCH(q)。為了保證εt2 為正值,要求a0 >0 ,ai ≥0 i=2,3,4… 。
上面(1)和(2)式構成的模型被稱為回歸-ARCH模型。ARCH模型通常對主體模型的隨機擾動項進行建模分析。以便充分的提取殘差中的信息,使得最終的模型殘差ηt成為白雜訊序列。
從上面的模型中可以看出,由於現在時刻雜訊的方差是過去有限項雜訊值平方的回歸,也就是說雜訊的波動具有一定的記憶性,因此,如果在以前時刻雜訊的方差變大,那麼在此刻雜訊的方差往往也跟著變大;如果在以前時刻雜訊的方差變小,那麼在此刻雜訊的方差往往也跟著變小。體現到期貨市場,那就是如果前一階段期貨合約價格波動變大,那麼在此刻市場價格波動也往往較大,反之亦然。這就是ARCH模型所具有描述波動的集群性的特性,由此也決定它的無條件分佈是一個尖峰胖尾的分佈。
ARCH模型的應用分析。從1982年開始就一直沒有間斷,經濟學家和計量經濟學家們,力圖通過不斷挖掘這個模型的潛力,來不斷增強我們解釋和預測市場的能力。從國外的研究情況來看,大致有兩個研究方向:
一是研究ARCH模型的拓展,完善ARCH模型。自ARCH模型始創以來,經歷了兩次突破。一次是Bollerslev T. 提出廣義ARCH (Generalized ARCH) , 即GARCH模型,從此以後,幾乎所有的ARCH 模型新成果都是在GARCH模型基礎上得到的。第二次則是由於長記憶在經濟學上的研究取得突破,分整研究被證明更有效地刻畫了某些長記憶性經濟現象,與ARCH模型相結合所誕生的一系列長記憶ARCH模型的研究從1996年至今方興未艾。
第二個應用是將ARCH模型作為一種度量金融時間序列數據波動性的有效工具,並應用於與波動性有關廣泛研究領域。包括政策研究、理論命題檢驗、季節性分析等方面。
ARCH模型能準確地模擬時間序列變數的波動性的變化,它在金融工程學的實證研究中應用廣泛,使人們能更加準確地把握風險(波動性),尤其是應用在風險價值(Value at Risk)理論中,在華爾街是盡人皆知的工具。
可以預見,未來的研究將會在方法論和工具論兩個方向進一步展開,特別是其應用研究還在不斷拓展,特別是伴隨著市場微觀結構理論的成熟,採用ARCH模型來模擬波動性,將會對期貨交易制度設計,風險控制制度設計和投資組合風險管理策略研究,提供一個更為廣闊的研究空間。
- 波勒斯勒夫(Bollerslev)提出GARCH模型(Generalized ARCH);
- 利立安(Lilien)提出ARCH-M模型;
- 羅賓斯(Robbins)提出NARCH模型








能把發展詳細解說一下嘛?謝謝