集中量數
用手机看条目
出自 MBA智库百科(https://wiki.mbalib.com/)
集中量數(measurement of control tendency)
目錄 |
[編輯]
什麼是集中量數[1]
集中量數亦稱數據的中心位置、集中趨勢，是指描述或反映集中趨勢的量數。
[編輯]
集中量數的概述[1]
集中量數是一組數據的代表值，能說明一組數據的典型情況。人們通常進行的測量，是想知道被測物體的真正有關數值，即真值。但是由於受許多主客觀條件的限制，不可能獲得這個真值。這樣，統計學中就用一些有代表性的數據末代替它，這些數據就是集中量數。
[編輯]
集中量數的內容[1]
包括：算術平均數，中位數、眾數、幾何平均數、調和平均數、加權平均數等。
[編輯]
集中量數的作用[1]
集中量數的作用：
(2)利用集中量數可研究總體的一般水平在時間上的變化。
(3)利用集中量數可分析現象之間的依存關係。
由於一組變數值的次數分佈有集中趨勢和離中趨勢，所以，單是集中量數不能反映一個分佈的全貌。因此，當用平均數描述集中趨勢時，應同時寫出標準差，用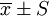
的形式表示整個分佈的概貌。
[編輯]
集中量數與差異量數的區別與關係[2]
集中量數與差異量數的區別與關係是，集中量數描述的是一組數據的典型情況，是一組數據的代表值；而差異量數描述的則是一組數據的離散情況，是一組數據的差異量。對於一組數據的全貌來說，差異量數愈大，集中量數的代表性就愈大。平均數的代表性如何，需要用差異量數來說明。
[編輯]
