隨機性決策
出自 MBA智库百科(https://wiki.mbalib.com/)
隨機性決策(decision under risk)
在不確定的狀態下,根據主觀概率和決策人的偏好對備選方案作出選擇的決策方法,又稱風險型決策。例如,在市場需要量不確定的情況下,分析和決定某種新產品應如何投產,就屬於隨機性決策。對隨機性決策問題進行決策,要藉助於兩個概念,即主觀概率和效用值。
主觀概率。客觀概率可通過在相同條件下重覆進行的隨機試驗來確定,而主觀概率只能由決策人根據自己的經驗和對事件所掌握的先驗信息來設定。例如,生產一定數量的某種產品並投放市場,有可能遇到三種狀態:暢銷、銷路一般和滯銷。在進行決策分析時,必須先對這三種狀態可能發生的概率進行估計。現在已經提出了一些設定主觀概率的方法。
效用值。隨機性決策問題需要對不同方案在各種狀態下可能產生的各種後果,分別確定它們的效用。用數值來度量效用稱為效用值。例如,對生產10萬件某種產品並暢銷,或生產50萬件某種產品並滯銷等後果,要賦予一定的效用值,才能作出定量分析。在不確定情況下作出決定都要冒一定的風險,因此確定後果的效用值總是和風險聯繫起來。各個決策人對冒風險所抱的態度不同,他們對同一後果會賦予不同的效用值。根據美國數學家J.von諾伊曼和O.莫根施特恩所建立的效用理論,在不確定情況下可用期望效用值作為效用的度量。
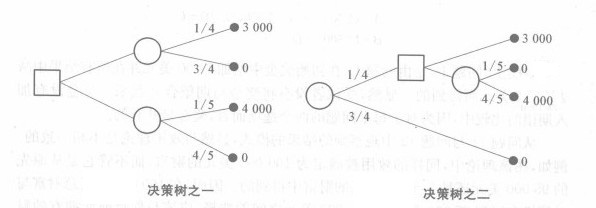
分析方法。分析一個具體的隨機性決策問題,首先應把決策標準、備選方案及其所處狀態,以及相應的主觀概率和後果效用值等因果關係用簡潔的模型描述出來。決策樹就是達到這個目的的一種手段。
例如,有一工廠擬生產某種產品,對生產量制定了三個方案,即a1=10萬件,a2=50萬件,a3=0萬件(即不生產)。預測投入市場後可能出現暢銷(θ1)、銷路一般(θ2)、滯銷(θ3)等三種狀態。不同方案在不同狀態下的主觀概率分別為pij,i、j=1,2,3;第i方案在j狀態下的後果效用值為C(ai,θj), i、j=1,2,3。這個隨機性決策問題可用圖中所示的決策樹來描述。圖中方塊節點表示決策節點,其後表示方案分枝;圓形節點表示狀態節點,其後表示狀態分枝;三角形節點表示後果節點,其後記上相應的後果效用值。最後通過簡單運算即可得到各方案的期望效用值,提供決策人進行決策。
貝葉斯分析。準確地設定主觀概率是件困難的事,因此在分析的過程中如能通過試驗收集更多的有關信息,並用以改進概率分佈,則更為理想。貝葉斯分析就能適應這一要求。貝葉斯分析的理論基礎是貝葉斯定理,這個定理的基本內容是:如果事件A和事件B有某種因果關係,A為“因”,而B為“果”,那麼就能通過對B的觀察,找到 A的概率。這樣確定的A的概率稱為後驗概率,而在觀察B之前所設定的A的概率稱為先驗概率。例如,農作物在生長季節獲得的降雨量的概率這個例子中,實際的降雨量為“因”,氣象預報為“果”,人們在聽到氣象預報之前對降雨量設的概率是先驗概率,在聽到氣象預報之後,根據貝葉斯定理推算得到的降雨量的概率是後驗概率。如果氣象預報有一定的準確性,後驗概率當然會比先驗概率準確。以貝葉斯定理為基礎的分析方法稱為貝葉斯分析,它是決策分析的基本方法。決策分析還有其他分析方法。