進化穩定策略
出自 MBA智库百科(https://wiki.mbalib.com/)
進化穩定策略(Evolutionarily stable stragegy,ESS)
目錄 |
進化博弈理論來自於達爾文的生物進化論,至少自雷威丁(Lewontin,1960)用於解釋生態現象就已經產生了。但直到1973年梅納德·史密斯和普萊斯(Maynard Smith and Price)、梅納德·史密斯(1974)提出了該理論的基本均衡概念——進化穩定策略及泰勒和喬克(Taylor and Joker)提出該理論的基本動態概念——模擬者動態以後,進化博弈理論得到了理論界的普遍關註。特別是1992年關於進化博弈理論發展的國際學術會議在康奈爾大學的召開,正式確定了進化博弈理論在經濟學上的學術地位,此後,該理論在經濟學便上獲得了迅速的發展及廣泛的應用。越來越多的經濟學家運用進化博弈理論來分析諸如社會制度變遷;阿克賽爾羅德(1984)、行業發展趨勢(波特,1980)、股市發展方向;利奈爾和羅爾、消費者對品牌的選擇、社會學習過程及社會習俗形成等領域的相關問題。進化穩定策略是進化博弈理論最基本的均衡概念,它具有廣泛的應用併在發展中得到了不斷完善。
在梅納德·史密斯和普萊斯(1973)、梅納德·史密斯(1974)提出進化穩定策略概念以前,進化博弈理論的發展還僅僅處於萌芽階段。在這一時期生態學家們主要應用純數學理論如極限環、分岔、奇異吸引子(Rosen,1970)等概念來描述生態演化系統並用於解釋生態現象,同時把生物之間的互動行為納入到進化模型之中(Wynne—Edwards,1962),他們的這種處理問題的方法已經蘊含了進化博弈理論的基本思想。在20世紀7O年代,生態學理論和博弈理論在各自領域中都獲得了迅速的發展,同時實驗經濟學作為一門學科也獲得了經濟學界的一致認同,這些條件為進化論與博弈論的結合提供了理論和現實基礎。生態學家梅納德·史密斯和普萊斯(1973)在總結以前理論的基礎上,提出進化博弈理論的基本均衡概念—— 進化穩定策略,該均衡概念的提出使得進化博弈理論的研究有了明確的方向,為進化博弈理論的進一步發展奠定了堅實的基礎。
所謂進化穩定策略也叫演化穩定策略,是指如果占群體絕大多數的個體選擇進化穩定策略,那麼小的突變者群體就不可能侵入到這個群體。或者說,在自然選擇壓力下,突變者要麼改變策略而選擇進化穩定策略,要麼退出系統而在進化過程中消失。下麵我們給出梅納德·史密斯和普萊斯(1973)所定義的進化穩定策略(參見張良橋,2001):
x∈A是進化穩定策略,如果y∈A,y≠x,存在一個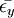 ∈(0,1),不等式u[x,εy + (1 − ε)x] > u[y,εx + (1 − ε)x]對任意e∈(0,
∈(0,1),不等式u[x,εy + (1 − ε)x] > u[y,εx + (1 − ε)x]對任意e∈(0,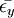 )都成立。其中A是群體中個體博弈時的支付矩陣;y表示突變策略;
)都成立。其中A是群體中個體博弈時的支付矩陣;y表示突變策略;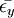 是一個與突變策略y有關的常數,稱之為侵入界限;εy + (1 − ε)x表示選擇進化穩定策略群體與選擇突變策略群體所組成的混合群體。從定義可以看出,當系統處於進化穩定狀態時(群體選擇進化穩定策略時所處的狀態就是進化穩定狀態),除非有來自外部強大的衝擊,否則系統就不會偏離進化穩定狀態,即系統會“鎖定”於該狀態。定義的直觀意思就是,當一個系統處於進化穩定均衡的吸引域範圍之內時,它就能夠抵抗來自外部的小衝擊。顯然,進化穩定策略是一個靜態概念,但它卻可以描述出系統的局部即吸引域內的動態性質。
是一個與突變策略y有關的常數,稱之為侵入界限;εy + (1 − ε)x表示選擇進化穩定策略群體與選擇突變策略群體所組成的混合群體。從定義可以看出,當系統處於進化穩定狀態時(群體選擇進化穩定策略時所處的狀態就是進化穩定狀態),除非有來自外部強大的衝擊,否則系統就不會偏離進化穩定狀態,即系統會“鎖定”於該狀態。定義的直觀意思就是,當一個系統處於進化穩定均衡的吸引域範圍之內時,它就能夠抵抗來自外部的小衝擊。顯然,進化穩定策略是一個靜態概念,但它卻可以描述出系統的局部即吸引域內的動態性質。
原初進化穩定策略定義為以後的研究者提供了理論基礎,但它是建立在許多理想化的假定之上,存在著許多不夠完善的地方:
第一,梅納德·史密斯等是在研究生態現象時提出的進化穩定策略概念的,由於動植物的行為完全是由其基因決定的。因而,每個種群體都被程式化為一個純策略,整個生態環境的所有種群也被看作一個大群體。然而,同一種群的個體由於其性別不同、需要不同、能力不同、基因突變或基因遺傳等因素都會影響到它們的行為,把每一個種群為程式化一個純策略是沒有太強說服力的,把一個生態環境中所有種群看作一個大群體也存在不妥之處;
第二,從梅納德·史密斯等提出的進化穩定策略定義可以看出,它僅適應於互不重疊且相互獨立的突變因素的影響,其吸引域半徑只與單個突變因素有關,也就是說只有等到一個突變因素對群體的影響消失之後,才能出現另一個突變因素,現實中出現這種現象是非常偶然的;
第三,梅納德·史密斯等為了技術上處理的方便及更好地利用數學工具和博弈論來描述生態演化過程而假定群體規模無限大,即隱含地假定博弈的支付空間是一個連通、閉集,這個假定不符合現實;
第四,從原初的進化穩定策略定義可以看出,它是一個靜態概念,只能描述系統(0,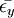 )的局部動態性質,沒有涉及到動態系統整體的調整過程,而現實中許多系統的均衡依賴於系統的整體動態性質。
)的局部動態性質,沒有涉及到動態系統整體的調整過程,而現實中許多系統的均衡依賴於系統的整體動態性質。
從生態意義上說,進化穩定策略把種群之間的互動行為納入到模型之中,推廣了達爾文的優勝劣汰理論,然而與納什均衡概念相比,進化穩定策略並不能解釋群體如何達到穩定的。它只能回答一旦達到了這種穩定狀態,原群體就對突變者群體者具有較強的抵抗力。也就是說,它只能回答當系統處於某一個均衡點的吸引域時,在一定條件下,隨著時間的演化,該系統就會趨於這個均衡點,而當系統有多重均衡或者多個均衡點或者多個吸引域時,原初的定義就顯得無能為力了。事實上梅納德·史密斯和帕克(Maynard Smith and Parker,1976)、梅納德·史密斯(1978,1979)已經認識到原初定義的某些缺陷,梅納德·史密斯(1982)給予了一定程度的修進並提出了修進的進化穩定策略概念。
梅納德·史密斯早在1979年就已經意識到,原初的進化穩定策略在處理多群體非對稱博弈時遇到了困難。他發現,在現實中,如生態學、經濟學和其他社會科學中的許多策略互動行為可能發生於兩個或多個群體的個體之間,個體之間進行的是非對稱博弈,單用原初定義不能很好解釋現實中的這些現象。如何把靜態的單群體進化穩定標準拓展到多群體情形呢?在單群體中,所有的個體都被程式化了一個純策略(梅納德·史密斯假定只有純策略是可以遺傳的),個體之間進行的是兩兩重覆匿名博弈;並且在單群體中,規模很少的突變因素對群體所產生的影響是可以忽略的,因此,非嚴格納什均衡策略不可能侵入到最優反應的嚴格納什均衡策略群體。在多群體中,突變因素可能來自於各個群體,突變策略者的互動行為會對群體行為產生不可忽略的影響。因此,原初的進化穩定標準僅僅限於嚴格納什均衡之間的選擇就不能運用於解釋多群體情形。
澤爾騰(Selten,1980)認為,把均衡概念由單群體拓展到多群體不是一個簡單的過渡,而是涉及到系統的動態調整過程及動態穩定性等一系列的變化。哈曼斯頓(Hammerstein,1981)認為,在非對稱博弈中,個體更加傾向於應用穩定策略來選擇行為並決定競爭結果,而這些穩定策略與進化穩定策略相比,可能會有更少的“吸引域”。因此,由進化穩定策略定義所得的結論就顯得有點似是而非了,但他沒有作出進一步解釋。
澤爾騰(Selten,1980))首次深入地研究了非對稱博弈動態穩定性並利用兩群體博弈情形證明“在非對稱博弈原初進化穩定策略必定是嚴格納什均衡”。後來,範代蒙(Van Damme,1987)在更一般的情形下證明瞭這個命題。我們知道,嚴格納什均衡本來就顯示出很好的性質,如果一個理論把其主要的註意力集中於研究嚴格納什均衡,那麼它就沒有任何理論價值;更重要的是許多非對稱博弈根本就不存在嚴格納什均衡,因而也就無法研究動態系統的穩定性;在非對稱博弈中,漸近穩定性實質上也蘊含了嚴格納什均衡,因此,漸進穩定性在非對稱博弈中也不是一個合適概念;進化穩定策略是一個靜態概念,雖然能夠描述系統的局部動態性質,但在非對稱博弈中,原初的進化穩定均衡與動態演化過程極限結果之間的對應關係卻不明顯(即出現了局部與全局的矛盾)。因此,要研究非對稱博弈的動態穩定性就必須通過考察系統的動態演化過程來尋求能夠適應於對稱博弈與非對稱博弈的穩定性概念。為了能夠更精確地描述非對稱博弈,澤爾騰(1983,1988)通過對引入角色限制行為而提出了適應於非對稱博弈的FAS概念。
他的定義如下:在有角色限制的博弈G中,一個行為策略s = (s1,s2)稱為進化穩定策略,
如果:(i)對任意的s'∈S×S,滿足f(s,s)≥f(s',s);
(ii)如果f(s,s)=f(s',s)那麼對任意的s≠s'有(s',s)>f(s',s')。
然而,澤爾滕的進化穩定策略概念儘管適應於描述兩群體非對稱博弈的情形,但它只能描述系統的局部動態性質,而且該定義並不能夠顯示出均衡概念與動態演化過程極限結果之間的關係。因此,要更好地描述非對稱博弈均衡,就必須正確處理好均衡概念與動態演化過程均衡結果之間的關係。於是,弗里德曼(Friedman,1991)考察了非對稱博弈的更一般的單調調整過程並得出了四個基本結論:
(1)每一個納什均衡都是動態系統的靜止點;
(2)漸近穩定結果必定是納什均衡;
(3)在對稱和非對稱博弈中,對所有單調調整過程而言ESS不一定是漸近穩定的;
(4)對某些單調調整過程而言,正規FAS是漸近穩定的。在此基礎上,他得出了“漸近穩定結果必定是納什均衡”結論。萊瑞·薩繆爾森和張建波(Larry Samuelson and Jianbo ,1992)在弗里德曼(1991)的基礎上進一步考察了非對稱博弈的累積單調選擇動態並得出:在非對稱博弈中,單調調整過程能夠剔除所有嚴格劣的純策略,並且能夠確保均衡結果必定是納什均衡。同時,他們證明瞭“穩定點必定是納什均衡”及“漸近穩定結果必定是嚴格納什均衡”,進而強化了弗里德曼(1991)的“漸近穩定結果必定是納什均衡”的結論。
Swinkels(1992)認為,進化穩定標準不對突變策略組合給予適當限制是說不過去的。特別地,在處理某些經濟問題時,突變策略可能來自於參與人或者企業的創新、試驗等活動,這些突變策略組合本身可能會影響系統的穩定性。因此,考察相對於後進入突變群體最優反應策略組合的穩定性可能會更合理,並且這些穩定性概念很容易由單群體情形推廣到多群體N一人非對稱博弈。於是他定義了適應於非對稱博弈的策略穩健性概念。
定義: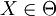 稱之為相對於均衡進入者的穩健策略(Robust against Equilibrium Entrants,REE),如果存在
稱之為相對於均衡進入者的穩健策略(Robust against Equilibrium Entrants,REE),如果存在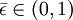 所有的策略組合y≠x及
所有的策略組合y≠x及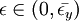 滿足:
滿足:![y\not\in\beta[\epsilon y+(1-\epsilon)x]](/w/images/math/2/1/8/218eaa306708fa44bde2260e94f6a8cd.png) 。
。
其中 表示突變策略;ε表示選擇突變策略者在群體中所占的比例;w = εy + (1 − ε)x表示混合群體;β[εy + (1 − ε)x]表示突變策略相對於策略X的最優反應策略,他並且證明瞭穩健策略是進化穩定策略的一個子集。然後,他又把穩健策略概念推廣到了N一人非對稱博弈的情形而提出了均衡進化穩定概念:
表示突變策略;ε表示選擇突變策略者在群體中所占的比例;w = εy + (1 − ε)x表示混合群體;β[εy + (1 − ε)x]表示突變策略相對於策略X的最優反應策略,他並且證明瞭穩健策略是進化穩定策略的一個子集。然後,他又把穩健策略概念推廣到了N一人非對稱博弈的情形而提出了均衡進化穩定概念:
定義:稱集合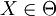 是均衡進化穩定的,如果它是相對於下麵性質的最小集:X是納什均衡策略集合ΘNE個非空閉子集,存在
是均衡進化穩定的,如果它是相對於下麵性質的最小集:X是納什均衡策略集合ΘNE個非空閉子集,存在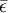 ∈(0,1),如果x∈X,
∈(0,1),如果x∈X, ,
,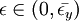 及
及![y\in\beta[(1-\epsilon)x+\epsilon y]](/w/images/math/2/4/b/24b4ba07f619f5e4bb032b9281e2f1ff.png) ,那麼
,那麼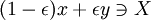 。
。
換句話說,均衡進化穩定集是納什均衡策略集的最小閉集,它能夠保證任何小規模的均衡進入突變者不可能使得群體離開進化穩定均衡的吸引域。
梅納德·史密斯等提出的進化穩定策略概念另一個缺陷就是,他們為了在技術上處理的方便而認為群體規模無限大,這個假定與現實尤其應用於解決經濟問題時並不相符。為了使理論與現實更接近,許多博弈論理論家對有限群體的均衡問題進行了深入的研究。
沙弗爾(Schafer,1988)首次放開群體規模無限大的假定,考察了有限規模群體的進化穩定性並提出了有限群體進化穩定策略概念。他證明“在一般情況下,有限群體進化穩定策略並不是納什均衡策略”。
漢森和薩繆爾森(Hansen and Samuelson,1988)分析了經濟博弈的演化過程,並把有限群體進化穩定策略稱之為“普遍生存策略”。他們認為,在現實世界競爭中,未來的利潤和可供選擇的策略具有不確定性,這就會阻礙企業選擇最優化策略,企業必須通過不斷的試驗、學習過程來尋求有利可圖的滿意策略(不一定是最優策略)。
沙弗爾(1989)應用“普遍生存策略”來研究寡頭企業之間的競爭並得出結論:通過經濟自然選擇過程而得以生存下來的策略是相對的而不是絕對的利潤最大化策略。
泰尼克(Tanaka,2000)利用模擬者動態,考察了差別產品對稱寡頭企業競爭的情形並定義了“全局生存策略”。他得出結論的是:在價格與數量競爭的寡頭模型中,全局生存策略都是隨機穩定的並且在兩種情況下它們是等價的。
以上所得到的均衡概念基本上是適應於單群體有限個體情形,並不適應於有限個體多群體博弈。哈佛保爾和西格蒙德(Hotbauer and Sigmund,l988)證明瞭“兩群體對稱博弈中不存在混合策略進化穩定策略”。澤爾騰(1988)在考察了大量的兩人對稱博弈的基礎上也得出了類似的結論。克瑞斯曼(1992)定義了有限兩群體非對稱博弈的進化穩定策略,1996年對他所定義的概念作了進一步說明。他認為,在模擬者動態下,至少一個群體的突變者所得到的平均支付少於選擇穩定策略者所獲得的支付,才能保證靜止點的漸近穩定性。格雷和瓦格(Garay and Varga,2000)認為,定義有限數目多群體的均衡概念應該滿足如下三點:
其一是突變者不能侵入他自己的群體;
其二是現有群體對來自外部的隨機衝擊具有較強的抵抗力;
其三是多群體進化穩定策略定義應該與非對稱博弈理論的基本結論一致。
眾所周知,純策略模擬者動態的漸近穩定集並不一定是進化穩定策略。那麼,哪一種動態穩定概念等價於進化穩定策略呢?克瑞斯曼(1990)指出,在單群體條件下強穩定性等價於進化穩定策略,那麼多群體的進化穩定策略定義也應該滿足多群體穩定性概念等價於多群體進化穩定策略。根據這個標準,格雷和瓦格(2000)定義了嚴格N群體進化穩定策略概念。其定義 如下:
定義:策略組合 稱之為N一群體進化穩定策略,如果對每一個
稱之為N一群體進化穩定策略,如果對每一個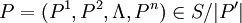 ,若
,若 ,Pi≠Pi' ,存在
,Pi≠Pi' ,存在 ,對所有的
,對所有的 都有:
都有:
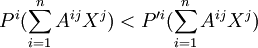
其中Xi = (1 − εj)P'j + εjPj 表示第j個混合群體(即選擇純策略Pj與P'j個體組成的群體);Aij表示i,j兩群體個體博弈時第i個群體中個體所得的支付矩陣。這個定義的優越性主要表現在:
(1)它與達爾文優勝劣汰理論是一致的,並且較好地解決了梅納德·史密斯(1982)及哈佛保爾和西格蒙德(1988)定義不適用於多群體問題;
(2)澤爾騰(1980)與哈佛保爾和西格蒙德(1988)的定義不能用於描述單群體情形,因為在單群體時由他們的定義得到系統沒有內點,在這裡引進了混合策略就能夠解決這個矛盾。他們認為,個體可能不能識別有不同策略集的對手,也可能不能確定他所選擇的策略是否依賴於他們對手策略集,因而引入混合策略是合理的;
(3)從動態的觀點來說,這裡的定義由於能夠確保在模擬者動態下的進化穩定策略的漸近穩定性,所以它也與單群體進化穩定策略概念是一致的。但他們的定義也存在一定的缺陷,該定義不僅要求突變因素 是相互獨立的,而且也要求突變率εj的變化是相互獨立的。在這一點上還沒能跳出傳統定義的框架。
梅納德·史密斯等提出的進化穩定策略概念第三個缺陷是要求突變因素是不連續且不重疊的。原初進化穩定策略定義由於僅僅考慮單個因素對系統的影響,所以任何偏離均衡狀態的行為都會隨著時間的演化自動回覆到原來的進化穩定狀態。帕克和菲爾德曼(Peck and Feldman,1988)認為,由於群體規模和後代數目很大,因而隨機因素對動態系統的影響是可以忽略不計的。現實並不是這樣,經濟演化系統常常會受到來自突變和其他偶然事件的衝擊,這些因素可能會對系統產生不可忽略的影響。
福斯特和楊(Foster and Young,1990)認為,首先,進化穩定策略概念把影響系統的因素都看成是一個個孤立的事件,而在現實中系統常常會受到連續的隨機衝擊。如果假定有一個因素的影響消失以後,再考慮另一個因素對系統的影響,那麼,系統當然就不會遠離原來的均衡狀態;其次,現實中出現上述情況純屬偶然現象,一個只能處理偶然現象的理論是沒有任何存在價值。現實中,儘管單個隨機因素對動態系統的影響較少,但它們卻可能對系統產生累積作用而定量地改變系統的穩定性,使得系統離開進化穩定狀態,系統什麼時候回覆到當初的進化穩定狀態,依賴於動態過程的全局結構,而進化穩定策略定義是一個局部概念,因此在考慮隨機衝擊時就不能作為判斷系統穩定性的標準;再次,由於系統的極限行為依賴於初始條件,同時在吸引子集合中只有一部分狀態是隨機穩定的,且隨機穩定狀態的選擇還依賴於隨機過程特定的結構,因此,進化穩定策略和一般意義上的吸引子由於沒有充分地考慮到隨機因素對進化系統的影響,在描述隨機系統的穩定性時也很不理想。於是,他們首次把影響系統的隨機因素納入到進化模型之中並提出了一個既不同於傳統進化穩定策略也不同於吸引子概念的隨機穩定性概念。他們的定義如下:
定義:群體向量P'是隨機穩定的,如果隨著隨機影響delta→0,極限密度對P'的每一個小鄰域都賦有正概率;更精確
地說,Vε>0, 其中N(P')=|P:|P—P'|<ε。其中fdelta(·)是當t→∞時,P(t)的極限分佈,delta表示隨機因素對系統所產生的影響。
其中N(P')=|P:|P—P'|<ε。其中fdelta(·)是當t→∞時,P(t)的極限分佈,delta表示隨機因素對系統所產生的影響。
粗略地說,一個狀態P是一個隨機穩定的,如果在長期中,隨著隨機衝擊因素影響的不斷變少,系統幾乎一定不會離開P的任意少的鄰域。隨機穩定的群體向量總是存在的,它有如下性質l隨著及delta→0及t→∞,它是一個最小閉集。接著,他們又提出了更一般的概念—— 隨機穩定集。隨機穩定集S是一個滿足如下條件的狀態集合,即從長期來看,隨著隨機衝擊的不斷變少,系統幾乎一定處於包含於S的任何一個開鄰域中。隨機穩定集概念的提出把傳統確定性動態模型中的進化穩定策略拓展到隨機性動態系統中,並且它是一個比進化穩定策略集更精練的概念,是進化穩定集的子集。隨機穩定集已經成為描述隨機動態系統的基本均衡概念。
從進化穩定策略的定義可以看出,它只能描述系統的局部動態性質而與系統的全局動態過程無關,然而,要更準確地描述一個系統的動態性質就必須對仔細考察整個系統的動態調整過程。泰勒和喬克(Taylor and Jonker,1978)首次把傳統的進化穩定策略定義用模擬者動態模型表示出來,他們證明在一個多群體的模型中,進化穩定策略是漸近穩定的充分但非必要條件。但他們沒有作出進一步的研究。鑒於此,吉爾博和馬特休(Gilb0a and Matsui,1991)在考察群體行動態調整過程的基礎上,提出了“迴圈穩定集”又一均衡概念。“迴圈穩定集”直接來源於群體行為的調整過程,其基本思想是“可接近性”。一個策略分佈f稱為可以從另一個策略分佈g接近是指,如果存在一條從f到g的道路,且在該道路方向上任何一點都是相對於該點的最優反應。
“迴圈穩定集”是指在滿足“可接近性”條件下是封閉的策略分佈集合(在該集合中任何兩個分佈之間都是接近的)。與一般均衡理論不同,僅當參與人按照均衡策略而作出選擇時才有效,迴圈穩定集並不要求群體保持這種決策狀態。迴圈穩定集的直觀意義是,在一個很短的時間間隔內,只有少部分人離開或者死亡並且由一些新來的人(新生的孩子)代替,這些新來者從他們的母體那裡繼承一些行為模式,並且在現行預期(也就是說他們並不關心行為模式未來的變化)條件下作出最優的反應,一旦新來者選擇了某一行動,他就會一直堅持下去(轉換成本的存在是他堅持這個行動的一個重要原因)。馬特休(1992)給出了一個“穩定”策略的靜態表述,在存在對原群體中各策略的初始分佈衝擊的情況下該策略能夠保持這種分佈。斯溫克斯(1992)在馬特休的基礎上提出了“群體穩定策略”。
相對於均衡的進入者而言,所謂“群體穩定策略”是指如果存在一個突變群體(或者進入者群體,譬如說群體A),其支付高於原群體的支付,那麼必定存在另外一個群體(如群體B),在這個包含大部分原群體個體而有一少部分群體A的個體的群體中,群體B將獲得高於群體A的支付。這個概念也稱為“穩健策略組合”。當然在某些情況下,“群體穩定策略”可能並不存在,但不是這個概念本身的缺點,出現這種情況與我們所研究的動態過程本身是分不開的。然而,我們可能會問,實際的行為模式又是怎麼樣呢?如果這個過程並不是穩定狀態,那麼穩定狀態又是什麼呢?在對這個問題作出回答時,馬特休利用了吉爾博和馬特休(1991)所提出的集值解的概念,同時他也證明瞭迴圈穩定集的存在性。Binmore and Samue1.son(1993)把參與人的學習過程納入到了進化模型中並提出了自我強化均衡(Fudenberg,D.,1998)。他們認為,每個參與人都會通過自己的經驗來推斷對手可能選擇的策略而作出最優反應,這個學習過程可能使得系統在不同自我強化均衡的吸引域之間漂移而不會停留在某一個均衡,由於在非均衡路徑上的推斷不一定正確,所以自我強化均衡可能不一定是納什均衡。








是不是應該把重點另起一行……密密麻麻看不下去……