肯德爾和諧繫數
出自 MBA智库百科(https://wiki.mbalib.com/)
肯德爾和諧繫數(the kandall coefficient of concordace)
目錄 |
肯德爾和諧繫數是計算多個等級變數相關程度的一種相關量。前述的spearman等級相關討論的是兩個等級變數的相關程度，用於評價時只適用於兩個評分者評價N個人或N件作品，或同一個人先後兩次評價N個人或N件作品，而kandall和諧繫數則適用於數據資料是多列相關的等級資料，即可是k個評分者評(N)個對象，也可以是同一個人先後k次評N個對象。通過求得kandall和諧繫數，可以較為客觀地選擇好的作品或好的評分者。
肯德爾和諧繫數的公式與計算[1]
以下用W表示肯德爾和諧繫數
(1)同一評價者無相同等級評定時，W的計算公式：
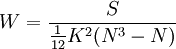(1)
式中：N—被評的對象數； K—評分者人數或評分所依據的標準數；
S—每個被評對象所評等級之和Ri與所有這些和的平均數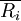
的離差平方和，即
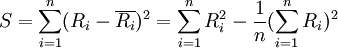
當評分者意見完全一致時，S取得最大值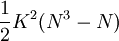
可見，和諧繫數是實際求得的S與其最大可能取值的比值，故0≤W≤1。
(2)同一評價者有相同等級評定時，W的計算公式：
![W=\frac{S}{\frac{1}{12}[K^2(N^3-N)-K\sum_{i=1}^K T_i]}](/w/images/math/d/c/b/dcb1e6ff8a53b302a1fdb1dc2315c3d2.png)
(2)
式中K、N、S的意義同(1)式，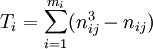
這裡mi為第i個評價者的評定結果中有重覆等級的個數，nij為第i個評價者的評定結果中第j個重覆等級的相同等級數。
對於評定結果無相同等級的評價者，Ti = 0，因此只須對評定結果有相同等級的評價者計算Ti。
【例1】 某校開展學生小論文比賽，請6位教師對入選的6篇論文評定得獎等級，結果如下表所示，試計算6位教師評定結果的kandall和諧繫數。
| 論文編號 評等 評分老師 | 一 | 二 | 三 | 四 | 五 | 六 | |
| A | 3 | 1 | 2 | 5 | 4 | 6 | |
| B | 2 | 1 | 3 | 4 | 5 | 6 | |
| C | 3 | 2 | 1 | 5 | 4 | 6 | |
| D | 4 | 1 | 2 | 6 | 3 | 5 | |
| E | 3 | 1 | 2 | 6 | 4 | 5 | |
| F | 4 | 2 | 1 | 5 | 3 | 6 | |
| Ri | 19 | 8 | 11 | 31 | 23 | 34 |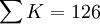 
|
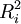 | 361 | 64 | 121 | 961 | 529 | 1156 |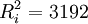 
|
解：由於每個評分老師對6篇論文的評定都無相同的等級，故用公式(1)，由表中數據得：
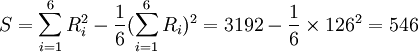
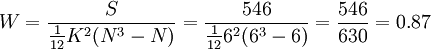
(由W=0.87表明6位老師的評定結果有較大的一致性)
【例2】 3名專家對6篇心理學論文的評分經等級轉換如下表所示，試計算專家評定結果的肯德爾和諧繫數
| 論文 等級 專家 | A | B | C | D | E | F | |
| 甲 | 1 | 4 | 2.5 | 5 | 6 | 2.5 | |
| 乙 | 2 | 3 | 1 | 5 | 6 | 4 | |
| 丙 | 1.5 | 3 | 1.5 | 4 | 5.5 | 5.5 | |
| Ri | 4.5 | 10 | 5 | 14 | 17.5 | 12 | 63 |
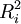| 20.25 | 100 | 25 | 196 | 306.25 | 144 | 791.5 |
解：由於專家甲、丙對6篇論文有相同等級的評定，故用公式(2)計算W：
甲T = 23 − 2 = 6
丙T = (23 − 2) + (23 − 2) = 12
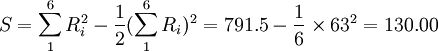
![W=\frac{S}{\frac{1}{12}[K^2(N^3-N)-K\sum T_i]}=\frac{130}{\frac{1}{12}[3^2(6^3-6)-3\times(6+12)]}=\frac{130}{153}=0.849673203=0.85](/w/images/math/1/d/e/1de22e9de9610bd1a179e8e4d219d8f4.png)
由W=0.85可看出專家評定結果有較大的一致性。
1、當評分者人數(k)在3-20之間，被評者(N)在3-7之間時，可查《肯德爾和諧繫數(W)顯著性臨界值表》，檢驗W是否達到顯著性水平。若實際計算的S值大於k、N相同的表內臨界值 ，則W達到顯著水平。
例如例3中，K=6 N=6，查表得檢驗水平分別為α = 0.01，α = 0.05的臨界值各為S0.01 = 282.4，S0.05 = 221.4，均小於實算的S=546，故W達到顯著水平，認為6位教師對6篇論文的評定相當一致。
2、當被評者n＞7時，則可用如下的x2統計量對W是否達到顯著水平作檢驗。
設H0：評價者意見不一致
則：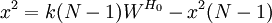
(3)
對給定的水平α，由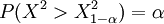
,查df=N-1的X2分佈表得臨界值為分位數
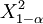，將計算出的kandall繫數W等代入(3)式計算X2值
若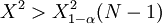
則拒絕H0，認為評分者的意見顯著一致。
若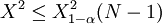
則H0認為評分者的評判顯著不一致。
例如，在一次教學評價中，10位評價者對12項指示進行評價，已計算出W=0.65，需檢驗評價者的意見是否有顯著的一致性(α = 0.01)。
將k=10 N=12 W=0.65代入(3)計算得
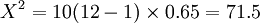
查表得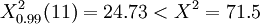
故認為10位評價者對12個指標的評價具有顯著的一致性。
- ↑ 楊宗義.教育統計學[M].科學技術文獻出版社,1990年08月第1版.
評論(共13條)
例2中S的計算有錯誤，應該為791-（63*63）/6=130
謝謝指正，已對相應內容做了修訂。
MBA智庫百科是大家可以參與編輯的百科，期待你的加入哦~
例2，Ti的計算，有點疑問，按照公式 好像分別是 6×6 和 12×12 啊
不好意思 好像是 甲T：6×6 丙T：6×6 + 6×6
給出的Ti值計算公式有誤，應該把平方去掉。
下麵的例子中計算是正確的，也就是沒有算平方的。
謝謝指正，原文已修正！並附上參考文獻，希望對您有幫助！
MBA智庫百科是眾人參與編輯和修改的百科，必然會造成一些不足，現已將參考文獻添加，希望對你有幫助。
例2中S的計算有錯誤，應該為791-（63*63）/6=130