斯皮爾曼等級相關
出自 MBA智库百科(https://wiki.mbalib.com/)
斯皮爾曼等級相關(Spearman Rank Correlation)
目錄 |
斯皮爾曼等級相關是根據等級資料研究兩個變數間相關關係的方法。它是依據兩列成對等級的各對等級數之差來進行計算的,所以又稱為“等級差數法”。
斯皮爾曼等級相關對數據條件的要求沒有積差相關係數嚴格,只要兩個變數的觀測值是成對的等級評定資料,或者是由連續變數觀測資料轉化得到的等級資料,不論兩個變數的總體分佈形態、樣本容量的大小如何,都可以用斯皮爾曼等級相關來進行研究。
斯皮爾曼等級相關係數[1]
斯皮爾曼等級相關係數是反映兩組變數之間聯繫的密切程度,它和相關係數r一樣,取值在-1到+1之間,所不同的是它是建立在等級的基礎上計算的。
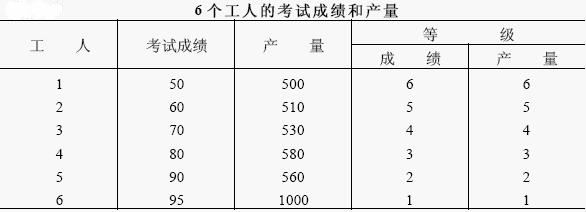
現結合一個例子來加以說明,某工廠對工人的業務進行了一次考試,欲研究考試成績與每月產量之間是否有聯繫,若隨機抽選了一個樣本,其考試成績和產量數字如下表:
從表中的數字可以看出,工人的考試成績愈高其產量也愈高,二者之間的聯繫程度是很一致的,但是相關係數r=0.676 並不算太高,這是由於它們之間的關係並不是線性的,如果分別按考試成績和產量高低變換成等級(見上表第3、4列),則可以計算它們之間的等級相關係數為1。計算等級相關係數可以將數據變換成等級以後用原有的相關係數公式計算,也可以將算出每一對樣本的等級之差di,然後用下列公式計算:
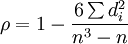
在所舉的例子中由於等級完全一致,所有的di = 0,所以r=1。等級相關係數和通常的相關係數一樣,它與樣本的容量有關,尤其是在樣本容量比較小的情況下,其變異程度較大,等級相關係數的顯著性檢驗與普通的相關係數的顯著性檢驗相同。
- ↑ 倪加勛,袁衛. 8.6 其他非參數統計方法.應用統計學.中國人民大學出版社.第262頁








好東東,謝謝熱心的朋友