箱線圖

出自 MBA智库百科(https://wiki.mbalib.com/)

箱線圖(Box plot)

　　箱線圖（Boxplot）也稱箱須圖（Box-whisker Plot），是利用數據中的五個統計量：最小值、第一四分位數、中位數、第三四分位數與最大值來描述數據的一種方法，它也可以粗略地看出數據是否具有有對稱性，分佈的分散程度等信息，特別可以用於對幾個樣本的比較。

　　（1）畫數軸

　　（2）畫矩形盒 兩端邊的位置分別對應數據的上下四分位數矩形盒：端邊的位置分別對應數據的上下四分位數（Q1和Q3）。在矩形盒內部中位數位置畫一條線段為中位線。

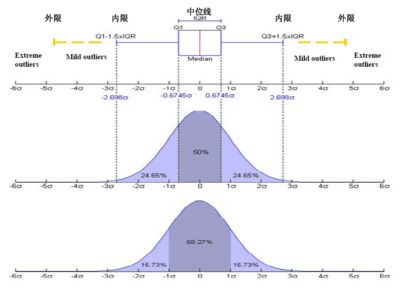
　　（3）在Q3＋1.5IQR（四分位距）和Q1-1.5IQR處畫兩條與中位線一樣的線段，這兩條線段為異常值截斷點，稱其為內限；在Q3＋3IQR和Q1－3IQR處畫兩條線段，稱其為外限。處於內限以外位置的點表示的數據都是異常值，其中在內限與外限之間的異常值為溫和的異常值（mild outliers），在外限以外的為極端的異常值(li)的異常值extreme outliers。

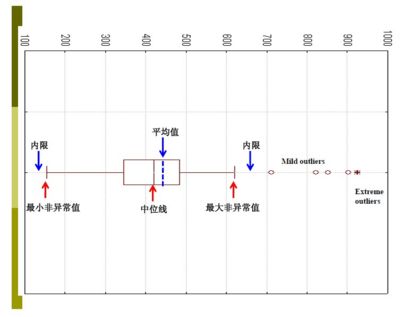
　　（4）從矩形盒兩端邊向外各畫一條線段直到不是異常值的最遠點 表示該批數據正常值的分佈區間點，示該批數據正常值的分佈區間。

　　（5）用“〇”標出溫和的異常值，用“＊”標出極端的異常值。

　　（統計軟體繪製的箱線圖一般沒有標出內限和外限。）

【例】^[2]12位商學院畢業生月起薪的樣本在這裡按升序重覆如下。

　　2710 2755 2850 | 2880 2880 2890 | 2920 2940 2950 | 3050 3130 3325

　　Q₁ = 2865　Q₂ = 2905(中位數)　Q₃ = 3000

　　中位數是2 905，第一個四分位數Q₁ = 2865，第三個四分位數Q₃ = 3000。檢查這些數據，最小值為2710，最大值為3325。因此，薪水數據的五數概括數據為2710、2865、2905、3000、3325。大約1／4或25％的觀察值在五數概括的相鄰兩個數字之間。

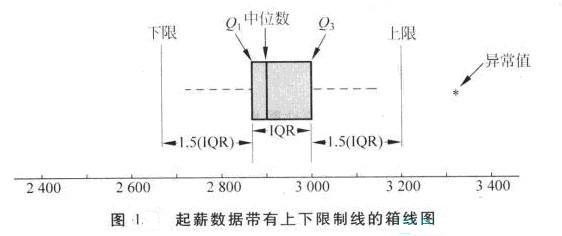
　　箱線圖是在五數概括的基礎上對數據進行描述的圖形方法。繪製箱線圖的關鍵是計算中位數、四分位數Q₁和Q₃。也可以使用四分位數全距IQR = Q₃ − Q₁。圖1是月起薪數據的箱線圖。

　　繪製箱線圖的步驟如下：

　　1．畫一隻箱子，箱子兩端分別位於第一個和第三個四分位數上。對於薪水數據來說,Q₁ = 2865以及Q₃ = 3000。這個箱子包括中間50％的數據。

　　2．在箱子中位數(薪水數據是2905)的位置畫一條垂直線。

　　3．用四分位數全距IQR = Q₃ − Q₁，確定限制線的位置。箱線圖的上、下限制線分別在比Q₁低1.5(IQR)和比Q₃高1.5(IQR)的位置上。對於薪水數據來說，IQR = Q₃ − Q₁ = 3000 − 2865 = 135。因此，限制線的位置在2865 − 1.5(135) = 2662.5和3000 + 1.5(135) = 3202.5處。兩條限制線以外的數據可以認為是異常值。

　　4．圖1中的虛線稱為觸鬚線。觸鬚線從箱子兩端開始繪製，直至第3步中計算的限制線內的最小值和最大值。因此，薪水數據的觸鬚線分別在2 710和3 130處結束。

　　5．最後，每個異常值的位置都用星號“*”表示出來。在圖1中，我們可以看到一個異常值，即3325。

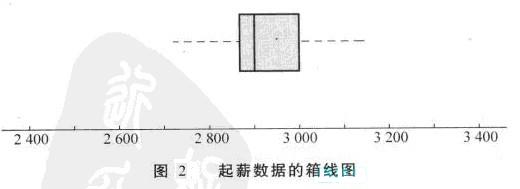
　　在圖1中，我們畫出了表示上下界限位置的直線。畫這些線是為了說明如何計算薪水數據的限制線並標出其位置。雖然限制線通常要計算出來，但是在箱線圖中一般並不標示出來。圖2顯示了薪水數據的常見箱線圖的形狀。

　　箱線圖作為描述統計的工具之一，其功能有獨特之處，主要有以下幾點：

　　1.直觀明瞭地識別數據批中的異常值

　　一批數據中的異常值值得關註，忽視異常值的存在是十分危險的，不加剔除地把異常值包括進數據的計算分析過程中，對結果會帶來不良影響；重視異常值的出現，分析其產生的原因，常常成為發現問題進而改進決策的契機。箱線圖為我們提供了識別異常值的一個標準：異常值被定義為小於Q1－1.5IQR或大於Q3＋1.5IQR的值。雖然這種標準有點任意性，但它來源於經驗判斷，經驗表明它在處理需要特別註意的數據方面表現不錯。這與識別異常值的經典方法有些不同。眾所周知，基於正態分佈的3σ法則或z分數方法是以假定數據服從正態分佈為前提的，但實際數據往往並不嚴格服從正態分佈。它們判斷異常值的標準是以計算數據批的均值和標準差為基礎的，而均值和標準差的耐抗性極小，異常值本身會對它們產生較大影響，這樣產生的異常值個數不會多於總數0.7%。顯然，應用這種方法於非正態分佈數據中判斷異常值，其有效性是有限的。箱線圖的繪製依靠實際數據，不需要事先假定數據服從特定的分佈形式，沒有對數據作任何限制性要求，它只是真實直觀地表現數據形狀的本來面貌；另一方面，箱線圖判斷異常值的標準以四分位數和四分位距為基礎，四分位數具有一定的耐抗性，多達25%的數據可以變得任意遠而不會很大地擾動四分位數，所以異常值不能對這個標準施加影響，箱線圖識別異常值的結果比較客觀。由此可見，箱線圖在識別異常值方面有一定的優越性。

　　2.利用箱線圖判斷數據批的偏態和尾重

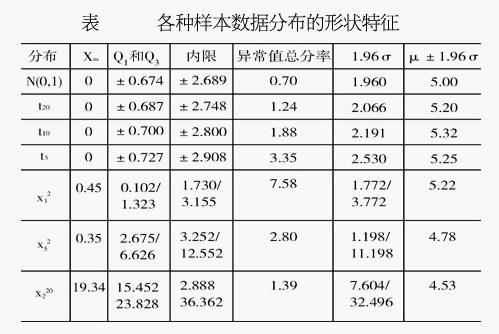
　　比較標準正態分佈、不同自由度的t分佈和非對稱分佈數據的箱線圖的特征，可以發現：對於標準正態分佈的大樣本，只有 0.7%的值是異常值,中位數位於上下四分位數的中央,箱線圖的方盒關於中位線對稱。選取不同自由度的t分佈的大樣本，代表對稱重尾分佈，當t分佈的自由度越小，尾部越重，就有越大的概率觀察到異常值。以卡方分佈作為非對稱分佈的例子進行分析，發現當卡方分佈的自由度越小，異常值出現於一側的概率越大，中位數也越偏離上下四分位數的中心位置，分佈偏態性越強。異常值集中在較小值一側，則分佈呈現左偏態；；異常值集中在較大值一側，則分佈呈現右偏態。下表列出了幾種分佈的樣本數據箱線圖的特征（樣本數據由SAS的隨機數生成函數自動生成），驗證了上述規律。這個規律揭示了數據批分佈偏態和尾重的部分信息，儘管它們不能給出偏態和尾重程度的精確度量，但可作為我們粗略估計的依據。

　　3.利用箱線圖比較幾批數據的形狀

　　同一數軸上，幾批數據的箱線圖並行排列，幾批數據的中位數、尾長、異常值、分佈區間等形狀信息便昭然若揭。在一批數據中，哪幾個數據點出類拔萃，哪些數據點表現不及一般，這些數據點放在同類其它群體中處於什麼位置，可以通過比較各箱線圖的異常值看出。各批數據的四分位距大小，正常值的分佈是集中還是分散，觀察各方盒和線段的長短便可明瞭。每批數據分佈的偏態如何，分析中位線和異常值的位置也可估計出來。還有一些箱線圖的變種，使數據批間的比較更加直觀明白。例如有一種可變寬度的箱線圖，使箱的寬度正比於批量的平方根，從而使批量大的數據批有面積大的箱，面積大的箱有適當的視覺效果。如果對同類群體的幾批數據的箱線圖進行比較，分析評價，便是常模參照解釋方法的可視圖示；如果把受測者數據批的箱線圖與外在效標數據批的箱線圖比較分析，便是效標參照解釋的可視圖示。箱線圖結合這些分析方法用於質量管理、人事測評、探索性數據分析等統計分析活動中去，有助於分析過程的簡便快捷，其作用顯而易見。

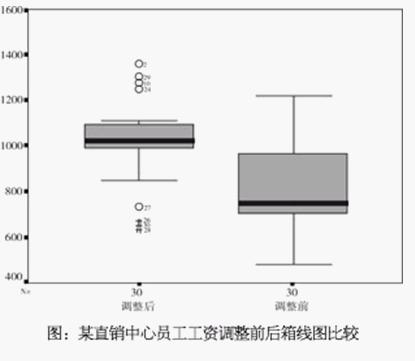
　　現有某直銷中心30名員工的工資測算數據兩批，第一批為工資調整前的數據，第二批為工資調整後的數據，繪出它們的箱線圖（如下圖），進行比較，可以很容易地得出：工資調整前，總體水平在752元左右，四分位距為307.5，沒有異常值。經過調整後，箱線圖顯示，第2、29、10、24、27號為溫和的異常值，第26、30、28號為極端的異常值。為什麼會出現異常值呢？經過進一步分析知道，第2、29、10、24號員工由於技能強、工齡長、積累貢獻大、表現較好，勞苦功高，理應得到較高的報酬；第27、26、30、28號職工則因為技能偏低、工齡短、積累貢獻小且表現較差，得到的工資較低，甚至連一般水平也難以達到。這體現了工資調整的獎優罰劣原則。另外，調整後工資總體水平比調整前高出270元，四分位距為106，工資分佈比調整前更加集中，在合適的範圍內既拉開了差距，又不至於差距太懸殊，還針對特殊情況進行了特殊處理。這種工資分佈具有激勵作用，可以說工資調整達到預期目的。

　　箱線圖美中不足之處在於它不能提供關於數據分佈偏態和尾重程度的精確度量；對於批量較大的數據批，箱線圖反映的形狀信息更加模糊；用中位數代表總體平均水平有一定的局限性等等。所以，應用箱線圖最好結合其它描述統計工具如均值、標準差、偏度、分佈函數等來描述數據批的分佈形狀。

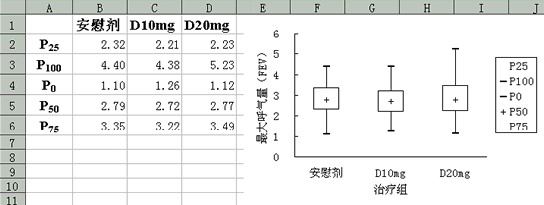
　　例：某研究者分別採用安慰劑、新藥10mg、新藥20mg 治療三個隨機分組的阻塞性肺病病人，每組100 例，治療兩周後測量最大呼氣量（forced expiratory volume, FEV）。每組測量後計算獲得的P100、P75、P50、P25、P0（即最大值、75%百分位數、中位數、25%百分位數、最小值**）（見下圖），試繪製箱線圖。

　　三種方案治療阻塞性肺病後的最大呼氣量箱線圖

　　繪製箱線圖需要藉助於股價圖中的“開盤-盤高-盤低-收盤圖”，該圖形需要將數據按一定的順序排列。因此繪製箱線圖時也需要將數據按P25、P100、P0、P50、P75的順序排列（P25與P75的順序可對調）。具體繪製步驟如下：

　　①選取單元格區域A1:D5，單擊“圖表嚮導”圖標如果圖片縮小請點擊放大，在彈出的“圖表類型”對話框中選中股價圖的“開盤-盤高-盤低-收盤圖”（第2 個子圖表類型），按下一步鍵。

　　②在圖表數據源對話框的數據區域中將“系列產生在”修改為“行”，按下一步鍵。

　　③在“圖表選項”對話框的分類（X）軸下方填入“治療組”，在數值（Y）軸下方填入“最大呼氣量（FEV）”，按完成鍵。

　　④在繪圖區點擊右鍵，選取“數據源→系列→添加”，在“名稱”右側用滑鼠選取單元格A6，在“值”右側用滑鼠選取單元格區域B6:D6 按確定鍵。

　　⑤在網格線上點擊右鍵，“清除”網格線；在繪圖區單擊右鍵“清除”背景色。

　　⑥在橫坐標上單擊右鍵，選取“坐標軸格式→圖案”，右上部主要刻度線類型覆選“無”，按確定鍵。

　　⑦在縱坐標上單擊右鍵，選取“坐標軸格式→數字→數值”，小數位數改為“0”，按確定鍵。

　　⑧在箱的中心位置P50 系列標誌上單擊右鍵，選取“數據系列格式→圖案”，在界面右側數據標記的樣式處選取“+”，前景顏色處選黑色，“大小”改為6 磅，按確定鍵；在箱線圖的頂部P100系列標誌上單擊右鍵，選取“數據系列格式→圖案”，在界面右側數據標記的樣式處選取長橫線“－”，前景顏色處選黑色，“大小”改為6 磅，按確定鍵；在箱線圖的底部P0系列標誌上單擊右鍵，選取“數據系列格式→圖案”，在界面右側數據標記的樣式處選取長橫線“－”，前景顏色處選黑色， “大小”改為6 磅，按確定鍵。

　　⑨適當調整繪圖區的大小，調整整個圖表區域的字體大小，去除圖表區的邊框等，可獲得上圖右側的箱線圖。

• 註：這五個值可以在Excel中用QUARTILE(array,quart)函數求得。由此處也可知，用Excel作箱線圖實際上也是一種間接的方式，並不是像SPSS等軟體那樣直接生成，從統計的角度來說，更重要的是這種方法不考慮Outliers，所以與其他軟體作出來的圖可能並不一樣。

　　1、不能提供關於數據分佈偏態和尾重程度的精確度量

　　2、對於批量比較大的數據批，反應的形狀信息更加模糊

　　3、用中位數代表總體評價水平有一定的局限性