特雷納－布萊克模型

出自 MBA智库百科(https://wiki.mbalib.com/)

　　證券分析是積極的資產組合管理的一種常用形式。如果研究單個證券，可能會發現許多定價不當的證券。它們給投資者提供了數值為正的預期α值。但是把資產組合全部集中在這些證券上將承擔本可以通過分散投資而減少的公司風險。因此，作為一個積極型投資經理，必須在大膽利用定價不當的證券和分散投資目標之間做出權衡。

　　特雷納與布萊克為證券分析的運用提供了一個優化模型，這種資產組合管理理論假定證券市場接近於有效率，該模型的要點是：

　　1.假定積極型投資管理基金的證券分析只能深入研究整個市場中相對較少的一部分股票，而其他沒有被分析的證券的價格是合理的。

　　2.為了有效地分散投資，市場指數資產組合是所有投資的基準，模型把它當作消極型資產組合。

　　3.投資管理公司的巨集觀預測部門應該提供消極型（市場指數）資產組合回報率與方差的預測值。

　　4.證券分析的目標是用有限數量的證券構造一個積極型資產組合，定價不當的被研究證券就是這種組合的基本組成部分。

　　5.分析人員應該按照以下步驟來構造這個積極型資產組合，並對其預期成果進行評價：

• 　　估計出每隻被分析證券的β值和它的殘差風險，根據β值與的巨集觀預測值確定該證券的必要回報率。
• 　　根據每隻證券定價不當的程度確定它的預期收益與預期超額收益（α值）。
• 　　不充分分散投資的成本為定價不當股票的非系統風險，即該股票殘值的方差。這種風險抵消了對價格低估證券進行專門研究所帶來的好處（α值）
• 　　根據α、β與殘差風險的估計值確定每隻證券在資產組合中的最佳權重。
• 　　根據資產組合中每隻證券的權重估計出該積極型資產組合的α、β與殘差風險。

　　6．根據消極型市場指數資產組合的巨集觀經濟預測值與積極型資產組合的綜合預測值確定最佳風險資產組合，它將是消極型資產組合和積極資產組合的結合。

• 　　如同不理想的市場時機也有巨大價值一樣，特雷納與布萊克提出的這種證券分析也具有潛在價值。所以，即使這種證券分析離精確還差很遠，但恰當的積極管理總有增值能力。
• 　　特雷納-布萊克模型在理論上很容易操作，而且即便把它的一些筒化假定放寬，它仍然大有作為。
• 　　該模型特別適用於分權化的機構中，而這正是使大型企業高效運轉的精髓所在。

　　假設所有證券的定價都是合理的，使用指數模型作為這些合理定價證券回報率的參考，那麼，第i個證券的回報率為：

　　r_i = r_f + β_i(r_M − r_f) + e_i.......（8-20）

　　其中， 是均值為0的隨機擾動項。

　　不考慮證券分析，特雷納與布萊克（TB）用式（8-20）表示所有證券的回報率，並且假定市場資產組合M是有效資產組合，而且證券之間回報率中的非系統部分 是不相關的。關於市場時機，TB假定消極型資產組合的預測已經做出，所以市場指數資產組合的預期回報率e_i和它的方差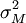都是已知的。

　　現在，我們只需考察目標證券集合中的一小部分，目的是在這些被分析證券中構造一個積極資產組合，並把這個組合與指數資產組合混合起來。對每一隻證券，其回報率可以寫成：

　　r_k = r_f + β_k(r_M − r_f) + e_k + a_k

　　其中，a_k表示定價不當證券的超出預期的額外收益。所以，對每一隻被分析證券，都要估計以下參數：

　　a_k,β_k,σ²(e_k)

　　如果所有的a_k均為0，那麼只需要進行消極管理就可以，指數資產組合M就是投資的最好選擇。但這種可能性極小，因為總存在不為0的a_k，有些為正，有些為負。

　　下麵，我們繼續分析持有積極型資產組合以後的工作，以便對特雷納—布萊克模型有一個整體印象。假定某一積極型資產組合A已經被構造出來了，並具有以下參數：

　　a_A,β_A,σ²(e_A)

　　它的總方差等於系統方差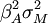與非系統方差σ²(e_A)的和，它與市場指數資產組合M的協方差為：

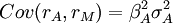
　　下麵我們來看這個優化過程的數學原理，如果我們把一部分資金w投資於積極型資產組合，另一部分資金1-W投資於市場指數資產組合。那麼，該組合的回報率為：

　　r_p(W) = Wr_A + (1 − W)r_M

　　我們可以用這個等式計算出夏普測度的數值（用超額回報均值除以它的標準差），它是權重W的一個函數。然後找到使夏普測度最大的最佳權重w。得到的最終結果為：

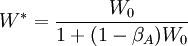　　.......（8-21）

　　其中