相對收益
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
相對收益又叫積極收益Alpha(簡稱α)、超額收益(ER)或執行收益(implementation return),通常用經理人增加Alpha的能力對他們進行評價,超額收益代表的是總收益超過無風險收益或基準收益的部分。
相對收益的表現形式[1]
- (一)直接差額形式
1.與無風險收益相比的絕對超額收益,分為簡單形式和複合形式,分別為:
簡單形式:ER=Rp − Rf=ER
複合形式:由於(1+Rp)=(1+Rf)(1+ER),則ER=\frac{1+Rp}{1+Rf} - 1
2.與基準收益相比的相對超額收益形式,又叫收益增加值(value added)
ER=Rp − RB(相當於β=1);ER為正,表明承擔積極風險以獲取超額收益而不是僅僅獲得基準收益。
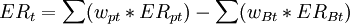
或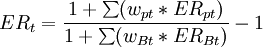
其中,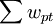 =1,
=1,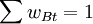
ERt表示組合在時間t超過基準組合的年化超額收益率,TE = σ(ERt)。
- (二)回歸形式
採用Beta衡量的市場波動進行風險調整的Alpha指標,包括回歸Alpha或Jensen’Alpha兩類。但有時投資報告中的Alpha或Beta。並不表明對Alpha或Beta的計算採用的是收益回歸分析還是超額收
益的CAPM模型計算出來的。因為回歸方法與CAPM模型算出來的繫數不同,含義解釋也不同,因此在計算和彙報風險時,對其進行區分是很重要的。在基準代表的市場收益給定的情況下,回歸繫數是對投資組合預期收益的統計描述;CAPM模型得到的收益和Alpha繫數分別是對組合收益的估計以及經理人超額收益的估計。具體包括:
1.回歸Alpha。可以採用單指數或多因素模型回歸:α = Rp − βRB + ε
在回歸Alpha的分析中,決定繫數R2反映了投資組合的分散化程度,便利起見將無風險利率處理為一常量,這樣R2其實就是系統風險在總風險比重。
實證分析發現,我國證券投資基金中R2的值介於0.1529~0.1853之間,說明非系統的風險仍較大,組合的分散化程度較低。
R2愈大,總風險中系統風險的比例愈高,組合的分散化程度越高。
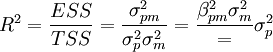 =系統風險/總風險
=系統風險/總風險
2.詹森Alpha:
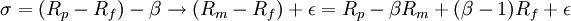
可見,簡單回歸Alpha中的基準收益RB包括市場組合Rm,完善的市場指數一般與基準是統一的。二者的區別在於,詹森Alpha比回歸Alpha多了(β − 1)RfRf≤O這一項。此外,回歸Alpha相當於β=1時的詹森Alpha。
此外,根據選取投資基準的不同,超額收益的表達式也不同。採取單一基準組合進行績效評估時,超額收益率為:
Rp − Rf = αp + βp(Rm − Rf) + εp
採取多個基準組合進行績效評估時,表達式為:
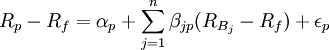
其中,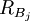 為第j個基準投資組合的收益率,βjp為目標投資組合超額收益率相對於第j個基準投資組合超額收益率的斜率繫數。
為第j個基準投資組合的收益率,βjp為目標投資組合超額收益率相對於第j個基準投資組合超額收益率的斜率繫數。
(三)總Alpha值(α)
業績評價中的總風險調整Alpha指標是法瑪將夏普比率中所使用的總風險調整法與詹森的收益率計算相結合提出的。公式為:
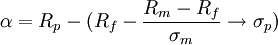
可見,總Alpha值足以資本市場線為依據進行計算的,這時組合的風險由其標準差表示。
- ↑ (美)皮爾遜著.風險預算[M].中信出版社,2011.03







