指數模型
出自 MBA智库百科(https://wiki.mbalib.com/)
我們將將單一證券的風險簡單的分為兩部分:市場風險(系統風險)和公司特有風險。相應地將證券的收益率寫成包含系統風險和公司特有風險的形式,而其中的系統風險可以用主要證券指數的收益來作為一般代表,我們稱這樣的收益率公式為指數模型。
目錄 |
我們把證券的持有期收益寫成:
ri = E(ri) + m + ei.............(1)
從而簡要地將巨集觀經濟因素與公司特有因素區分開。
式中:
- E(ri)——證券持有期期初的期望收益;
- m——證券持有期間非預期的巨集觀事件對證券收益的影響;
- ei——證券持有期間非預期的公司特有事件對證券收益的影響。
m和ei都具有零期望值,因為他們都是非預期事件的影響,根據定義其平均值必然為零。
如果我們記巨集觀因素的非預測成分為F,記證券i對巨集觀經濟事件的敏感度為βi,則證券i的收益的巨集觀成分為mi = βiF,則(1)式變成:
ri = E(ri) + βiF + ei............(2)
如果我們用主要證券指數,如標準普爾500指數作為巨集觀因素的一般代表時,就可得到與單因素模型類似的等式,這就是單指數模型,也就是我們將要討論的指數模型的一般代表。
指數模型的風險溢價形式
根據指數模型,我們可以把實際的或已實現的證券收益區分成巨集觀(系統)的與微觀(公司特有)的兩部分。我們把每個證券的收益率寫成三個部分的總和:
| 項目 | 記號 |
|
αi |
股票持有期超額收益可寫成:
ri − rf = αi + βi(rm − rf) + ei
我們用大寫的R代表超過無風險收益的超額收益,把這個等式改寫成:
Ri = αi + βiRm + ei
我們考慮單個證券的方差,有:
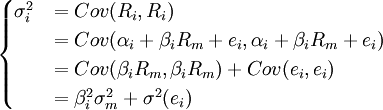
上式可做如下解釋:αi為一確定值,其與其它變數的協方差均為零;ei為公司特有成分,獨立於系統風險,即ei與Rm的協方差為零。從而得到上式。
我們考慮兩個證券的協方差,有:
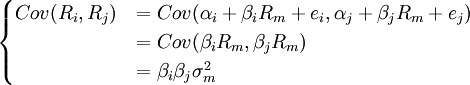
與前述方差的解釋一致,而且有兩公司的特有風險不相關,即存在Cov(ei,ej) = 0。
由夏普首先建立的指數模型也提供了資產組合風險分散化的另一個視角。假定我們選擇有n個證券的等權重資產組合。每個證券的超額收益率由下式給出:
Ri = αi + βiRm + ei
相似地,我們可以把股票資產組合的超額收益寫成:
Rp = αp + βpRm + ep................(3)
現在我們說明,隨著資產組合中的股票數量的增加,歸因於非市場因素的風險部分將變得越來越小。這部分風險被分散掉了。相比較,市場風險依然存在,無論資產組合的股票數量有多少。
我們註意到等權重的假定(即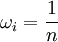 ),從而有:
),從而有:
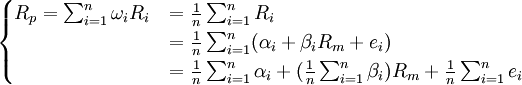 ………………(4)
………………(4)
比較上式與(3)式,我們可得到:
資產組合對市場的敏感度為:
資產組合有一個常數的非市場收益成分: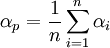
和零均值變數: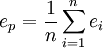
資產組合的方差為: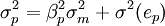
我們定義資產組合方差的系統風險成分為依賴於市場運動的部分為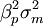 ,它也依賴於單個證券的敏感度繫數。這部分風險依賴於資產組合的貝塔的
,它也依賴於單個證券的敏感度繫數。這部分風險依賴於資產組合的貝塔的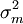 ,不管資產組合分散化程度如何都不會改變。無論持有多少股票,它們在市場中暴露的一般風險將反映在資產組合的系統風險中。
,不管資產組合分散化程度如何都不會改變。無論持有多少股票,它們在市場中暴露的一般風險將反映在資產組合的系統風險中。
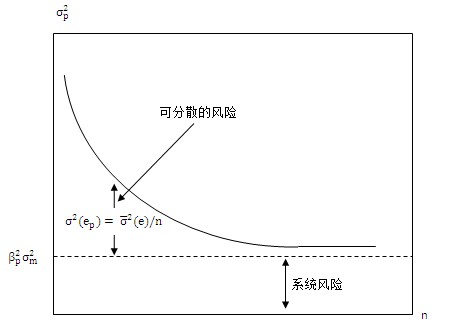
相比較,資產組合方差的非系統風險成分是σ2(ep),它來源於公司特有成分ei。因為這些ei是獨立的,都具有零期望值,所以可以由平均法則得出這樣的結論:隨著越來越多的股票加入到資產組合中,公司特有風險傾向於被分散掉,非市場風險越來越小,這些風險被認為是可分散的。這一點可說明如下。
因為ei是獨立的,有:
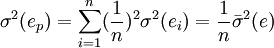
式中,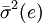 為公司特有方差的均值。由於這一均值獨立於n,所以當n變大時,σ2(ep)就變得小得可以忽略了。
為公司特有方差的均值。由於這一均值獨立於n,所以當n變大時,σ2(ep)就變得小得可以忽略了。
總而言之,隨著分散化程度的加強,資產組合的方差接近於系統方差。系統方差定義為市場因素的方差乘以資產組合敏感繫數的平方 。可見如下示意圖。
。可見如下示意圖。
由指數模型,有:
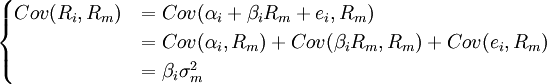
在上式中,我們註意到αi是一個常量,因而Cov(αi,Rm) = 0;而公司特有的成分獨立於整個市場的成分,因而Cov(ei,Rm) = 0。從而有:
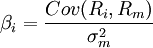
由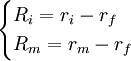
知:Cov(Ri,Rm) = Cov(ri,rm)
這說明指數模型與資本資產定價模型中的貝塔具有相同的含義。
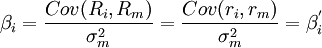 ,式中
,式中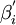 為
為







寫得非常好,比百度知道不知道強多少倍