核心存款
出自 MBA智库百科(https://wiki.mbalib.com/)
核心存款(core deposit)
目錄 |
什麼是核心存款[1]
核心存款又被稱為無到期日存款(non-maturity deposit)或流動性存款(liquidity deposit)。對於核心存款的定義,目前尚未形成統一的標準。
美國通貨監理局(Office of Comptroller of the Currency,簡稱OCC)認為,所謂核心存款就是指那些能夠穩定客戶關係的活期和定期存款,銀行可以在一定時期,通常是數年內使用這些資金。
Becher(1962),Parson(1972)以及Flannery(1982)認為,核心存款是指由於存在整置成本(setup cost,又譯為起動成本、整備成本等)和交易投資成本而使銀行和儲戶都願意繼續持有的那部分存款。
McGuire(1995)從儲戶的角度給出瞭如下的定義:核心存款是指那些主要用於滿足交易支付需求且可以隨時提取的存款。
縱觀上述定義,筆者認為,核心存款就是儲戶在銀行持有的對市場利率變動不敏感且可以隨時支取的那部分資金頭寸。
核心存款比率表現為核心存款和總資產比率以及核心存款和貸款總額的比率。
核心存款比例=核心存款/總資產
核心存款指那些相對來說比較穩定的,對利率變化不太敏感的存款,季節和經濟環境對其影響也較小,所以核心存款是銀行資金的穩定來源,這一比率反映了銀行流動性大小;
國外對核心存款的研究[1]
- 1.核心存款餘額的穩定性和長期性
一般認為,核心存款餘額對利率不敏感,因而比較穩定。Becher(1962),Oi(1962) 以及Parson(1972)發現,儲戶設立新帳戶(在銀行開設新帳戶)會產生整置成本,該成本會促使銀行和儲戶維持現有的關係。雖然從短期來看維持這種關係對雙方可能都不是最優的,但長期而言是最優選擇。Flannery(1982)的結論同上述觀點相似。他認為,簽署新的存款合同會同時給銀行和儲戶都帶來整置成本和學習成本。銀行在資金充裕時為了節約資金成本,就可減少核心存款餘額。但由於存在上述成本,再加上未來的資金需求量可能較大,所以銀行一般並不願意減少核心存款餘額。對於儲戶而言其原理也是相同的。筆者認為,核心存款體現了銀行和儲戶的互利關係:銀行樂意長期為儲屍提供各種優質服務,而儲戶也願意長期接受低於市場利率的存款收益。這種互利關係使得核心存款餘額的變動不會由於外界環境的變化麗發生很大的變化,因而核心存款的餘額比較穩定。
雖然核心存款餘額比較穩定,但由於核心存款可以隨時提取,所以它不像定期存款那樣有確切的到期日,如3年。Flannery和James(1984)指出,由於儲戶願意持有一定數量的核心存款來滿足日常交易以及應付突發事件產生的支付需求,因而核心存款具有較長的實際到期日。然而他們並未指出核心存款的具體到期日。對於商業銀行而言,只有準確地瞭解每一筆資金來源的期限才能合理地安排資金貸放,才能避免出現資金閑置或不足的問題。因而僅研究核心存款餘額具有較長的實際到期日是不夠的,商業銀行關註的是,“較長”到底有“多長”,3年還是5年,抑或10年。因此,測度核心存款餘額的實際到期日已成為學者們進一步研究的課題。
1993年,美國學者Chambers最先給出核心存款餘額的實際到期日。他的研究表明,核心存款的平均持有期是5年。在他之後還有不少學者對這一問題也進行了研究。Morgan和Cates(1994)的實證分析表明,通常銀行在8年後失去50%的核心存款儲戶,而在20年後則將失去所有的核心存款儲戶(不考慮新儲戶的加入)。就平均而言,核心存款的持有期為6—8年。他們的研究不僅給出了核心存款餘額的實際到期日,而且還得出“核心存款消亡的速度隨時間的推移而不斷降低”的重要結論。Berger和Udell(1995)的研究顯示,核心存款的實際到期日約為12年,而Pennacchi(1996)的實證結果是6年。從總體看,核心存款的實際到期日約為6年。造成Berger、Udell(1995)與其他學者結論不同的主要原因在於他們選取不同性質的樣本。在分析了他們所研究的銀行核心存款構成比例後,筆者發現,前者的研究對象,即所選取銀行的核心存款主要以個人活期存款帳戶為主,而後者所研究的對象則以企業活期存款帳戶為主。由於企業存款的金額較大,因而對利率的敏感性相對較高,其期限比個人活期存款短也屬正常。如此看來,儘管核心存款沒有確切的到期日,但其實際到期日卻非常長。因此,對於銀行而言,核心存款餘額具有穩定和長期的特性。同時,上述學者研究結論的分歧也告訴我們:在研究核心存款實際到期日的時候,應該將不同種類的核心存款,分別計算其實際到期日,這樣才能獲得比較準確的數據。
- 2.核心存款利率的決定因素及其特性
從錶面看,核心存款利率是由商業銀行直接制定的。實際上,銀行在制定這一利率時還需要考慮儲戶的反應和市場的狀況。Whitesell(1992)和Hutehison(1995)強調了儲蓄和交易功能在核心存款定價方面的重要性。他們認為,儲戶的儲蓄意願(與投資意願相對應)越強,核心存款的交易功能越多,則利率越低。 McGuire(1995)認為,商業銀行和儲戶的博弈決定核心存款的利率水平。商業銀行對核心存款附加服務的質量和便利程度是儲戶考慮的主要因素,而儲戶的偏好又決定了商業銀行在現行市場利率條件下制定一個最優利率。在一些經濟因素髮生變化以後,原來的均衡就會被打破,於是產生新一輪的博弈,最終達到一個銀行和儲戶都不願改變的現有策略的納什均衡點。
目前,更多的研究集中在核心存款利率的特性上。Small(1990),Harman和Berger(1991),Neumark和 Sharp(1992)以及Ausubel(1992),在分析了美國銀行的統計數據後指出,核心存款利率具有三個基本特征:一是核心存款利率低於市場利率(一般指一年期存款或國債利率);二是短期內核心存款利率呈現粘性(核心存款並不立即對市場利率的調整作出反應,其調整存在一定的時滯);三是從長期看核心存款利率調整趨勢不對稱(當市場利率上升時,核心存款利率並不隨之上升,呈現剛性特征;當市場利率下降時,核心存款利率隨之下降,呈現非剛性特征)。核心存款利率低於市場利率這比較容易理解,因為核心存款的流動性要高於一年期存款和國債,因而其收益率就相對較低。而短期內核心存款利率呈現粘性的觀點是由O’Brien (2000)提出的。他認為,從理論上講,在外部因素影響市場利率以後,核心存款利率應當隨之發生變動。但實際上,如果市場利率上升,銀行就提高核心存款利率,則會增加利息支出。為了控製成本,銀行就會降低對核心存款儲戶服務的質量,並減少服務種類。儲戶也意識到,如果存款的利息收益增加,那麼就不可能享受原先的優質服務,獲得的便利也會減少,因而儲戶樂意接受原先的利率。由於銀行和儲戶都不願改變原先的策略,核心存款利率在短期內就不會上升。同理,如果市場利率下降,銀行和儲戶也仍然會採取原來的策略,核心存款利率也不會隨之下降。所以,從實際情況來看,銀行不會因為市場利率的變動而頻繁調整核心存款利率,核心存款利率在短期內具有粘性。但從長期來看,核心存款利率具有不對稱調整的特性。Ausubel (1992)認為,信息有限以及搜尋成本的存在是核心存款利率不對稱調整的主要原因。其模型結論為當市場利率不斷下降時,商業銀行核心存款流失的概率也非常大。而實際情況是從長期看,當市場利率不斷上升時,儲戶由於受高利率的誘惑而不斷將核心存款轉向其他投資工具。Sharpe(1997)依據消費者搜尋成本的建模,解釋了核心存款利率調整不對稱的.原因,但他沒有提出明確的解決方案。Kahn等(1999)利用消費者的有限記憶試圖對存款利率調整進行解釋,但他們還是未能明確解釋核心存款利率為什麼在市場利率上升和下降時會出現不對稱調整的現象。時至今日,還沒有一位學者能夠合理地解釋這個問題。
- 3.核心存款的估價方法和溢價特性
國外金融機構在金融產品的定價及風險預測和防範管理方面,一般都傾向於運用定量模型。但核心存款的定量分析卻沒有一個類似於資本資產定價模型(CAPM)的標準模型,主要原因在於核心存款缺少一個具有高度流動性的二級市場。Ausubel(1991),Calera和Mester(1995)以及Hutchison和Pennaechi(1996)通過研究發現,核心存款之所以難以估價,是因為市場競爭不完全,商業銀行一般不會將其核心存款出售給其他銀行。同時,搜尋和轉換成本、監管壁壘以及逆向選擇問題等也使得核心存款的估價變得更加困難。
核心存款的估算[2]
- 1.HP濾波法原理
HP濾波法是由Hodrick和Prescott於1980年在分析美國戰後的經濟景氣時首先提出的。這種方法被廣泛地應用於對巨集觀經濟趨勢的分析研究中。HP濾波法是一種時間序列在狀態空間中的分析方法,相當於對波動方差的極小化。HP濾波可以看作是一個近似的高通濾波器(High-Pass Filter),其理論基礎是時間序列的譜分析方法。譜分析方法把時間序列看作是不同頻率的成分的疊加,時間序列的High-Pass濾波就是要在這些所有的不同頻率的成分中,分離出頻率較高的成分,去掉頻率較低的成分,也即去掉長期的趨勢項,而對短期的隨機波動項進行度量。
HP濾波的原理,可以表述為:
假設經濟時間序列為Y={y1,y2,…,yn},趨勢要素為G={g1,g2,…,gn}。其中,n為樣本的容量。因此,HP濾波可以將yt(t=1,2,…n)分解為:
yt = gt + ct
其中,gt和ct均為不可觀測值。
一般的,時間序列Y中不可觀測部分趨勢G常被定義為下麵(1)最小化問題的解:
![min \left\{ \sum_{t=1}^n (y_t - g_t)^2 + \lambda \sum_{t=1}^n [B(L)g_t]^2 \right\}](/w/images/math/8/1/f/81fb1842aba9b63c0b49ea69a88b75d2.png)
其中,B(L)是延遲運算元多項式
B(L) = (L − 1 − 1) − (1 − L)
將(2)代人(1)式,則HP濾波的問題就是使下麵損失函數最小,即
![min \left\{ \sum_{t=1}^n (y_t - g_t)^2 + \lambda \sum_{t=1}^n [(g_{t+1} -g_t)-(g_t - g_{t-1})]^2 \right\}](/w/images/math/8/a/d/8adba9d463ea5f7d9ccbeabfe46c2704.png)
對(3)式y1,y2,...,yn進行一階求導,並令導數為0,得:
g1: c1 = λ(g1 − 2g2 + g3)
g2: c2 = λ( − 2g1 + 5g2 − 4g3 + g4)

gt: ct = λ(gt − 2 − 4gt − 1 + 6gt − 4gt + 1 + g4)

gn − 1: cn − 1 = λ(gn − 3 − 4gn − 2 + 5gn1 − 2gn)
gn: cn = λ(gn − 2 − 2gn1 + gn)
用矩陣形式表示,為:
c = λFg
F為如下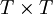 繫數矩陣:
繫數矩陣:

通過上述公式,可以得到:
y − g = λFg
整理後,可得:
g = (λF + I) − 1y
並且,在上述F矩陣中,每一列元素之和均為零。因此,根據C=\lambda Fg可知,短期波動之和為0。即:
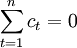
最小化問題用![\lambda \sum_{t=1}^n [B(L)g_t]^2](/w/images/math/c/b/9/cb9953e5f1be9a9a53e80ab5290e6391.png) 來調整趨勢的變化。並且,
來調整趨勢的變化。並且,![\lambda \sum_{t=1}^1[B(L)g_t]^2](/w/images/math/4/6/c/46c2be92a075f999079ff85f2595799e.png) 的取值隨著λ的增大而增大。不同的λ值決定了不同的隨機波動方式和不同的平滑程度。當λ = 0時,有gt = yt,滿足最小化問題的趨勢等於序列Y;隨著λ的增加,估計的趨勢越光滑;當λ→∞時,估計的趨勢也就接近於線性函數,這時,HP濾波就退化為用最小二乘法估計趨勢。從統計意義上講,λ的值的選取是任意的,因為任何一個非平穩時間序列都可以分解成為無數個非平穩趨勢成分與平穩周期成分的組合。但λ的取值決定著趨勢要素對實際序列的跟蹤程度和趨勢光滑度之間的權衡選擇。分別用
的取值隨著λ的增大而增大。不同的λ值決定了不同的隨機波動方式和不同的平滑程度。當λ = 0時,有gt = yt,滿足最小化問題的趨勢等於序列Y;隨著λ的增加,估計的趨勢越光滑;當λ→∞時,估計的趨勢也就接近於線性函數,這時,HP濾波就退化為用最小二乘法估計趨勢。從統計意義上講,λ的值的選取是任意的,因為任何一個非平穩時間序列都可以分解成為無數個非平穩趨勢成分與平穩周期成分的組合。但λ的取值決定著趨勢要素對實際序列的跟蹤程度和趨勢光滑度之間的權衡選擇。分別用 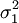 和
和 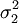 表示時間序列中趨勢成分和周期成分的標準差,那麼,λ的最優取值即為
表示時間序列中趨勢成分和周期成分的標準差,那麼,λ的最優取值即為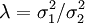 。根據一般經驗,\lambda的取值如下:
。根據一般經驗,\lambda的取值如下:
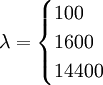
100,年度數據;1600,季度數據;14400,度數據
- 2.應用HP濾波法求核心存款
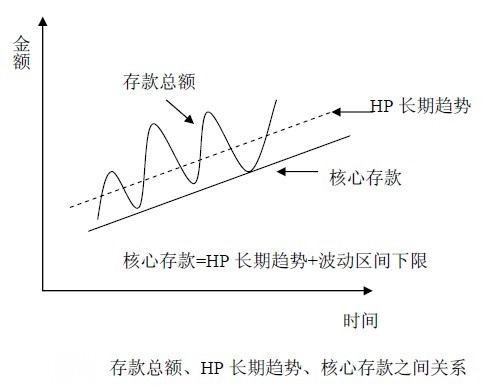
採用HP濾波方法計算出來的長期趨勢反映了商業銀行存款總額變動的平均狀態。實際存款總額總是圍繞長期趨勢而上下波動, 且由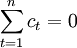 可以得知,各期波動存款之和為零。而我們所要求的核心存款是指存款中長期穩定部分, 波動存款在核心存款之上浮動。核心存款與波動存款之間具有關係:
可以得知,各期波動存款之和為零。而我們所要求的核心存款是指存款中長期穩定部分, 波動存款在核心存款之上浮動。核心存款與波動存款之間具有關係:
波動存款=存款總額-核心存款
因此, 用HP濾波求出的長期趨勢成分和短期波動成分並不是我們所需要的核心存款和波動存款,我們還需要在此基礎上做進一步計算,以得出穩定的核心存款金額。
為此,本文把用HP濾波法計算出來的長期趨勢做下移,從而以一定的概率保證實際存款總額總是在核心存款之上波動。
假設由HP濾波求得的波動部分ct滿足正態分佈N(μ , σ2),其中μ為ct的期望,σ2為方差。則由 和
和 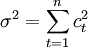 即可求得N(μ,σ2)。取存款總額在核心存款之上的概率為置信水平(1- α),滿足置信水平(1- α)的區間為(-C,C),則有:
即可求得N(μ,σ2)。取存款總額在核心存款之上的概率為置信水平(1- α),滿足置信水平(1- α)的區間為(-C,C),則有:
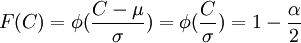
由於α、σ均為已知量,因此,可以反求出C。將HP濾波法求得的穩定部分gt向下平移C即得到核心存款:
核心存款= gt − C
如圖所示,存款總額、核心存款與通過HP濾波方法得到的長期趨勢之間具有如下關係: