無風險證券
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
無風險證券,是指能夠按時履約的固定收入證券,即沒有任何風險的證券。無風險證券的利率稱為無風險利率。在證券界通常將期限小於三個月的短期貼現國債視為無風險證券。
這是因為三個月的期限很短,在這期間市場利率波動對債券的影響很小,其收益基本是恆定的,可以認為是沒有風險的。
結合我國的情況,目前還沒有三個月的國庫券,因此無風險利率可以參照短期存款利率.
在現實中,人們通常將政府債券作為無風險證券的典型例子,這不僅因為政府債券往往是固定收入的證券,還因為政府債券在正常情況下政府所做的支付承諾能夠按計劃兌現。即使政府收不抵支,政府也可以通過發行貨幣來兌現支付承諾,不過此時投資者會面臨購買力風險。因此,無風險證券只是一種假定的證券。假定存在無風險證券,主要是為了說明無風險條件下,證券投資價值的決定機制。
在無風險的條件下,投資者購買固定收益證券,需要花費現期收入,從而必須推遲消費。雖然投資者在未來時期可以按時獲取固定的收入,但從投資購買證券到獲取收入之間始終存在一定的時差。投資者推遲消費的耐心應獲得報酬,這種報酬對投資本金的百分率便稱為貨幣的時間價值,即利息率,簡稱利率。貨幣的時間價值是使用貨幣的機會成本,或者說是無風險條件下使用貨幣進行投資可能獲得的收益,也可以說是貨幣的基本市場價格。各種證券投資都涉及到貨幣的時間價值。
無風險證券對有效邊界的影響
無風險證券對有效邊界的影響是:(幾何特征)現有證券組合可行域較之原有風險證券組合可行域擴大並具有直線邊界。
原因:
1、投資者通過將無風險證券F與每個可行的風險證券組合再組合的方式增加證券組合的種類,使原有風險證券組合的可行域得以擴大(新可行域含:無風險證券、原有風險證券組合、因無風險證券F與原有風險證券組合再組合而產生的新型證券組合);
2、無風險證券F與任意風險證券或組合P進行組合時,其組合線恰好是一條由無風險證券F出發並經過風險證券或組合P的射線FP,從而無風險證券F與切點證券組合T進行組合的組合線便是射線FT,併成為新可行域的上部邊界――有效邊界。
設F是無風險證券,其無風險收益率為rf,rf 是常數。又設S是風險證券,其期望收益率為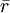 ,風險是σ。現作F和S的組合p=(x,1-x),其中x 是投資於無風險證券F的比例,如果不能賣空,則
,風險是σ。現作F和S的組合p=(x,1-x),其中x 是投資於無風險證券F的比例,如果不能賣空,則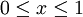 ;1-x是投資於風險證券S的比例。
;1-x是投資於風險證券S的比例。
下麵討論這個組合收益率、風險和和有效前沿。
F的風險為零,σf = 0。這樣,組合P的期望收益率和風險分別為:
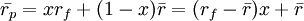
![\sigma_p=[x^2\sigma^2_f+2x(1-x)\sigma_{f_3}]^{y_2}](/w/images/math/c/9/2/c92bd91fc75500e6b7d585c91204ade8.png)
= (1 − x)σ
消去參數x,得到:
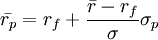
這個方程在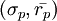 平面上表示的是一條直線,它在
平面上表示的是一條直線,它在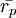 軸上的截距是rf ,斜率是
軸上的截距是rf ,斜率是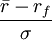 。位於F(0,rf) 和
。位於F(0,rf) 和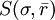 之間的線段是組合p=(x,1-x)的可行集和有效前沿,x=0對應於風險證券S,而x=1對應於無風險證券F 。
之間的線段是組合p=(x,1-x)的可行集和有效前沿,x=0對應於風險證券S,而x=1對應於無風險證券F 。







