排中律
出自 MBA智库百科(https://wiki.mbalib.com/)
排中律(Law Of Excluded Middle)
目錄 |
什麼是排中律[1]
排中律是指在同一個思維過程中,兩個互相矛盾的思想不能都假,必有一真。用公式表示為:“A或者非A”。這顯然是一種不相容的選言關係。即在同一思維過程中,或者A,或者非A,二者必居其一。違反排中律,就會在思維中犯“模棱兩可”的錯誤。
排中律的邏輯結構[2]
排中律實質是要求人們的思維具有明確性。具體來看它的邏輯結構,可以如下分析:
1.對於概念來說,某詞項所對應的概念總是或者反映了某個對象,或者沒有反映這一對象。用“A”來表示該詞項所對應的概念的話,那麼,對於任意一個對象來說,它總是或者屬於“A”的外延,或者屬於“非A”的外延。即在同一思維過程中,就同一對象而言,它或者是“A”,或者是“非A”,二者必居其一。排中律的公式可以表示為:“ ”。
”。
2.對於命題來說,排中律斷言:在同一思維過程中同一個命題(用P表示)或者是真的或者是假的。也就是說,如果否定了“P”為真,也就等於肯定了“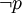 ”為真;如果否定了“P”為假,也就等於肯定了“
”為真;如果否定了“P”為假,也就等於肯定了“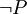 ”為假。用符號來重述它就是:排中律斷言的是每個具有
”為假。用符號來重述它就是:排中律斷言的是每個具有 形式的命題必定是真的,每個這樣的命題都是重言式。
形式的命題必定是真的,每個這樣的命題都是重言式。
從以上對排中律的內容和結構的分析中,可以看出,排中律要重言式。
從以上對排中律的內容和結構的分析中,可以看出,排中律要求思維的明確性,不允許在“是”與“非”之間含糊不清。否則,在思維或者是論辯過程中就會容易造成觀點或者主張的模棱兩可、令人費解。
違反排中律的邏輯錯誤[3]
根據排中律的要求,在同一思維過程中,對於矛盾關係或下反對關係的思想,不能都加以否定。如果都加以否定,就違反排中律。違反排中律要求的邏輯錯誤叫做“兩不可”,即對兩個相互矛盾的判斷都否定。這種邏輯錯誤,是對互相矛盾的思想沒能二者擇其一造成的。從其表現形式上看有以下兩種情況。
1.對互相矛盾或具有下反對關係的判斷都否定
這種邏輯錯誤是典型的“兩不可”錯誤,即是在同一時間、同一關係下,對同一對象做出的具有矛盾關係或下反對關係的判斷都加以否定的邏輯錯誤。如,有人說“可能有鬼”,有人說“可能無鬼”,我對這兩種觀點都不贊成,這種爭論沒有多大意思。“可能有鬼”和“可能無鬼”是兩個下反對關係的判斷,二者必居其一。同時否定,犯“兩不可”的邏輯錯誤。
2.對互相矛盾或具有下反對關係的判斷即不肯定也不否定
這樣的錯誤一般也把它稱為不置可否的錯誤。在生活中有這樣一種人,遇事不搖頭也不點頭,像魯迅先生的雜文《立論》中所講的事情:
一個家庭得子過滿月,主人高興之餘問來賓孩子的將來如何?甲說:“孩子將來定要發財。”乙說:“孩子將來定會做官。”兩人都得到了主人的獎賞。可丙卻說:“孩子將來定會死的。”結果惹了一頓打。在這種情況下,作者只好去問老師如何回答?老師說:“說要死的必然,說富貴的說謊。但說謊的得好報,說必然的遭打。你既不想說謊也不想挨打,那麼,你就說,啊呀!這個孩子呵!您瞧!多麼……阿唷!哈哈!Hehe!he,hehehehe!”’
在這段文字中不管是作者還是老師,他們都未能對兩個互相否定的判斷作出正確的回答。特別是老師採取“哈哈”的態度,既不肯定也不否定,這就是典型的不置可否的錯誤。
在日常生活和工作中,常見的在是非、真假問題上不敢鮮明地表明自己贊成什麼反對什麼,而是含含糊糊,迴避觀望,這種“好好先生”的毫無原則的態度,以及在兩種互相矛盾的意見之間需要做出決斷而不作決斷,卻互相推諉,毫無責任心的官僚主義態度,從邏輯的角度來看,也屬於違反排中律的模棱兩可的錯誤。
正確理解和運用排中律的保證[3]
(一)區分排中律的“中”與唯物辯證法的“中介”
排中律的“中”與唯物辯證法的“中介”是不同的,不要把二者混同。
(1)含義不同
排中律的“中”是指思維過程中“是”與“否”、“真”與“假”的中間情況,這種中間情況不是客觀存在,而僅僅是在人的思維過程中。唯物辯證法的“中介”是對客觀世界普遍存在的中間環節的客觀、正確的反映。也就是人們常說的中間環節。這種中間環節是真實的、普遍的,例如客觀世界中確實存在著“不上不下”、“不左不右”、“不前不後”、“亦此亦彼”、“非此非彼”的現象,這就是唯物辯證法的“中介”。因此在應用過程中不能誇大排中律的作用。
(2)意義不同
“中”不是邏輯學的範疇,是表現那種影響思維明確性的虛構存在的狀況,是排中律所要排除的對象,在“是”與“否”、“矛”與“盾”之中作出“非此即彼”的選擇。“中介”是唯物辯證法的重要範疇,它揭示了客觀事物的“亦此亦彼”的辯證性質,具有方法論意義。正確理解“中介”範疇,對於完整、準確地把握和運用對立統一規律有重要作用。
(二)正確理解排中律的本質
排中律是保證思維明確性的一條規則,它從思維不能“兩否”的角度補充了矛盾律的內容,進一步保證思維具有確定性。
排中律在實際運用中不僅有助於消除思維中的兩不可現象,保證思維的明確性,而且要求人們在真理與謬誤,是與非面前旗幟鮮明,不能猶豫。而詭辯者和堅持錯誤的人總是迴避在相互排斥的觀點之間作出明確選擇。運用排中律,就可以首先從邏輯上揭穿其詭辯手法,進而駁斥其觀點的謬誤。
人們不僅可以揭示對手的謬誤,而且可以用排中律進行推理和論證,從正面闡述我們的觀點。因為排中律是確認在同一思維過程中,兩個互相矛盾或具有下反對關係的判斷不能同假,必有一真,但到底哪個真不能確認,肯定有一個真的,也可能同真。所以,可以利用排中律進行推理和論證。
(三)運用排中律要註意以下幾個問題
①若不是在“同一思維過程”的條件下,對兩個互相否定的思想都加以否定,並不違反排中律。
②人們對於互相矛盾的判斷,由於認識或客觀實際的限制,暫時還不能分辯或回答,這種情況並不違反排中律。如,到底有沒有UFO?現在既不肯定也不否定。這是大家都知道的事實。
③當某個複雜問語所隱含的判斷不能成立或不能接受時,從而不用肯定或否定的方式來回答也不違反排中律。如有人問你“你現在還抽煙嗎?”這句話中就隱含著另外一個判斷,那就是“你以前抽煙”。無論你回答“是”或“不是”都得承認這個假定。這種問句,邏輯上稱之為複雜問句。碰上一個複雜問句,當其中包含的那個假定是不能接受的時候,不要輕易回答,否則,就會陷入對方的圈套中。
④區分與矛盾律的不同。
其一是適用範圍不同。矛盾律與排中律都針對兩個互相矛盾的判斷,但矛盾律還針對上反對關係;而排中律是對下反對關係的。
其二是內容不同。矛盾律指明“有假”,即指明兩個互相矛盾或具有上反對關係的判斷,不能同真,必有一假;而排中律是指明“有真”,即指明兩個互相矛盾或具有下反對關係的判斷,不能同假,必有一真。
其三是違反要求的錯誤不同。矛盾律不遵守規則導致的錯誤叫“模棱兩可”;而排中律不遵守規則導致的錯誤叫“兩不可”。
其四是實際作用不同。矛盾律是由真推假;而排中律是由假推真。
在瞭解了矛盾律與排中律的不同之後,就可以有條理地分析一個判斷到底是適用矛盾律還是排中律,包括這個判斷是否違反邏輯規律都是可以一目瞭然的。
首先,如果你遇到的兩個判斷具有上反對關係,那顯然就要用矛盾律;如果是具有下反對關係的兩個判斷,就要用排中律。
其次,如果同時斷定兩個互相矛盾的概念或判斷為真,則違反矛盾律;如果同時否定兩個互相矛盾的概念或判斷,則違反排中律。
總之,先看出現的是相互反對還是相互矛盾的概念或判斷還是下反對關係的判斷,再看對這些概念或判斷是同時加以肯定,還是同時加以否定。這樣就比較容易區分到底是違反了矛盾律還是排中律。
反證法(又稱歸謬法、背理法)是一種論證方式,他首先假設某命題不成立(即在原命題的條件下,結論不成立),然後推理出明顯矛盾的結果,從而下結論說原假設不成立,原命題得證。
反證法常稱作Reductio ad absurdum,是拉丁語中的“轉化到不可能”,源自希臘語中的“ἡ εις το αδυνατον παγωγη”,阿基米德經常使用它。
“歐幾裡得最喜歡用的反證法,是數學家最精良的武器。它比起棋手所用的任何戰術還要好:棋手可能需要犧牲一隻兵或其他棋,但數學家用的卻是整個游戲。”《一個數學家的辯解》,英國數學家高德菲·哈羅德·哈代。
維也納的科學哲學家卡爾·波普爾的論點:“不能被反證的理論就不能被稱作科學的理論”。(這裡的反證不是指反證法,而是指推翻如證偽、修正、提出異議等。
反證法在數學中經常運用。當論題從正面不容易或不能得到證明時,就需要運用反證法,此即所謂"正難則反"。牛頓曾經說過:“反證法是數學家最精當的武器之一”。一般來講,反證法常用來證明正面證明有困難,情況多或複雜,而逆否命題則比較淺顯的題目,問題可能解決得十分乾脆。應用反證法的是:欲證“若P則Q”為真命題,從相反結論出發,得出矛盾,從而原命題為真命題。
反證法是“間接證明法”一類,是從反方向證明的證明方法,即:肯定題設而否定結論,從而得出矛盾。法國數學家阿達瑪(Hadamard)對反證法的實質作過概括:“若肯定定理的假設而否定其結論,就會導致矛盾”。具體地講,反證法就是從反論題入手,把命題結論的否定當作條件,使之得到與條件相矛盾,肯定了命題的結論,從而使命題獲得了證明。 在應用反證法證題時,一定要用到“反設”,否則就不是反證法。用反證法證題時,如果欲證明的命題的方面情況只有一種,那麼只要將這種情況駁倒了就可以,這種反證法又叫“歸謬法”;如果結論的方面情況有多種,那麼必須將所有的反面情況一一駁倒,才能推斷原結論成立,這種證法又叫“窮舉法”。
原理1:給出命題P和命題(非P),根據排中律( ),兩者之中起碼有一個是真(更強的說法為,除了真和假之外並無其他的情況),所以若果其中一個是假的,另一個就必然是真。
),兩者之中起碼有一個是真(更強的說法為,除了真和假之外並無其他的情況),所以若果其中一個是假的,另一個就必然是真。
原理2:給出命題P和命題(非P),根據無矛盾律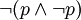 ,兩者同時為真的情況
,兩者同時為真的情況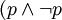 )為假。形式化為:
)為假。形式化為: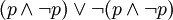 。與排中律的邏輯結構相同。
。與排中律的邏輯結構相同。
原理3:給出命題p和r,根據否定後件律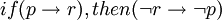 ,如果若成立p時出現r,則為r假時即為p假。
,如果若成立p時出現r,則為r假時即為p假。
反證法在要證明時,透過顯示出若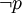 成立時出現矛盾,即為
成立時出現矛盾,即為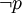 假,從而證明為P真。
假,從而證明為P真。
證明:命題P為真
詳細論證以下命題為真:
A.沉默是金
B.和氣生財
- 1.反命題為:話多是金。假設該命題為真。
- 2.舉出實際反例:
a.言多必失,禍從口入。話過多,把自己底牌亮出,讓自己處於信息不對稱的地位,暴露自己的隱私與弱點,陷入被動的境地,極易破財。
b.話多誤事,效率低下,浪費時間與精力,等同於破財。不節制說話的話,會忘記該做的事情。
c.話多容易造成重覆啰嗦甚至傷害人,十分討人厭,搞壞形象與人緣,等同於甚至甚於破財。一個只知道話多的人,他的思想是不會隨著話多而增加的。
d.即使是有些靠說話謀生的人,也不能話多。如,主持人,銷售員等,主要靠提問引導對方多說話而不是自己多說話。
e.話多不如話少,話少不如話精。人的內心是很隱密的,恭維了某個人可能就得罪了另一個人。 說話是門藝術,除了十分用腦,還要十分用心。心直口快,小事冒煙,大事冒火,是十分不用腦,十分不用心的表現,也是還沒學會自我控制的表現,最終吃虧的就是自己。
f. 實證分析一下:冷靜想想身邊熟悉的人。話多財多,話多破財,悶聲發財,悶聲破財。從人數和財富的數量上,對比這四種人中,有沒有典型代表,結論自然就能得出。
- 3.反命題:話多是金。該命題不成立。
- 4.據排中律:沉默是金。
- 5.和氣生財,大致同理。
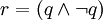 。據
。據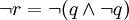








排中律,實質就是2選1。是排除法的特例。排除法是多選1。