排中律
出自 MBA智库百科(https://wiki.mbalib.com/)
排中律(Law Of Excluded Middle)
目录 |
什么是排中律[1]
排中律是指在同一个思维过程中,两个互相矛盾的思想不能都假,必有一真。用公式表示为:“A或者非A”。这显然是一种不相容的选言关系。即在同一思维过程中,或者A,或者非A,二者必居其一。违反排中律,就会在思维中犯“模棱两可”的错误。
排中律的逻辑结构[2]
排中律实质是要求人们的思维具有明确性。具体来看它的逻辑结构,可以如下分析:
1.对于概念来说,某词项所对应的概念总是或者反映了某个对象,或者没有反映这一对象。用“A”来表示该词项所对应的概念的话,那么,对于任意一个对象来说,它总是或者属于“A”的外延,或者属于“非A”的外延。即在同一思维过程中,就同一对象而言,它或者是“A”,或者是“非A”,二者必居其一。排中律的公式可以表示为:“ ”。
”。
2.对于命题来说,排中律断言:在同一思维过程中同一个命题(用P表示)或者是真的或者是假的。也就是说,如果否定了“P”为真,也就等于肯定了“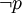 ”为真;如果否定了“P”为假,也就等于肯定了“
”为真;如果否定了“P”为假,也就等于肯定了“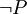 ”为假。用符号来重述它就是:排中律断言的是每个具有
”为假。用符号来重述它就是:排中律断言的是每个具有 形式的命题必定是真的,每个这样的命题都是重言式。
形式的命题必定是真的,每个这样的命题都是重言式。
从以上对排中律的内容和结构的分析中,可以看出,排中律要重言式。
从以上对排中律的内容和结构的分析中,可以看出,排中律要求思维的明确性,不允许在“是”与“非”之间含糊不清。否则,在思维或者是论辩过程中就会容易造成观点或者主张的模棱两可、令人费解。
违反排中律的逻辑错误[3]
根据排中律的要求,在同一思维过程中,对于矛盾关系或下反对关系的思想,不能都加以否定。如果都加以否定,就违反排中律。违反排中律要求的逻辑错误叫做“两不可”,即对两个相互矛盾的判断都否定。这种逻辑错误,是对互相矛盾的思想没能二者择其一造成的。从其表现形式上看有以下两种情况。
1.对互相矛盾或具有下反对关系的判断都否定
这种逻辑错误是典型的“两不可”错误,即是在同一时间、同一关系下,对同一对象做出的具有矛盾关系或下反对关系的判断都加以否定的逻辑错误。如,有人说“可能有鬼”,有人说“可能无鬼”,我对这两种观点都不赞成,这种争论没有多大意思。“可能有鬼”和“可能无鬼”是两个下反对关系的判断,二者必居其一。同时否定,犯“两不可”的逻辑错误。
2.对互相矛盾或具有下反对关系的判断即不肯定也不否定
这样的错误一般也把它称为不置可否的错误。在生活中有这样一种人,遇事不摇头也不点头,像鲁迅先生的杂文《立论》中所讲的事情:
一个家庭得子过满月,主人高兴之余问来宾孩子的将来如何?甲说:“孩子将来定要发财。”乙说:“孩子将来定会做官。”两人都得到了主人的奖赏。可丙却说:“孩子将来定会死的。”结果惹了一顿打。在这种情况下,作者只好去问老师如何回答?老师说:“说要死的必然,说富贵的说谎。但说谎的得好报,说必然的遭打。你既不想说谎也不想挨打,那么,你就说,啊呀!这个孩子呵!您瞧!多么……阿唷!哈哈!Hehe!he,hehehehe!”’
在这段文字中不管是作者还是老师,他们都未能对两个互相否定的判断作出正确的回答。特别是老师采取“哈哈”的态度,既不肯定也不否定,这就是典型的不置可否的错误。
在日常生活和工作中,常见的在是非、真假问题上不敢鲜明地表明自己赞成什么反对什么,而是含含糊糊,回避观望,这种“好好先生”的毫无原则的态度,以及在两种互相矛盾的意见之间需要做出决断而不作决断,却互相推诿,毫无责任心的官僚主义态度,从逻辑的角度来看,也属于违反排中律的模棱两可的错误。
正确理解和运用排中律的保证[3]
(一)区分排中律的“中”与唯物辩证法的“中介”
排中律的“中”与唯物辩证法的“中介”是不同的,不要把二者混同。
(1)含义不同
排中律的“中”是指思维过程中“是”与“否”、“真”与“假”的中间情况,这种中间情况不是客观存在,而仅仅是在人的思维过程中。唯物辩证法的“中介”是对客观世界普遍存在的中间环节的客观、正确的反映。也就是人们常说的中间环节。这种中间环节是真实的、普遍的,例如客观世界中确实存在着“不上不下”、“不左不右”、“不前不后”、“亦此亦彼”、“非此非彼”的现象,这就是唯物辩证法的“中介”。因此在应用过程中不能夸大排中律的作用。
(2)意义不同
“中”不是逻辑学的范畴,是表现那种影响思维明确性的虚构存在的状况,是排中律所要排除的对象,在“是”与“否”、“矛”与“盾”之中作出“非此即彼”的选择。“中介”是唯物辩证法的重要范畴,它揭示了客观事物的“亦此亦彼”的辩证性质,具有方法论意义。正确理解“中介”范畴,对于完整、准确地把握和运用对立统一规律有重要作用。
(二)正确理解排中律的本质
排中律是保证思维明确性的一条规则,它从思维不能“两否”的角度补充了矛盾律的内容,进一步保证思维具有确定性。
排中律在实际运用中不仅有助于消除思维中的两不可现象,保证思维的明确性,而且要求人们在真理与谬误,是与非面前旗帜鲜明,不能犹豫。而诡辩者和坚持错误的人总是回避在相互排斥的观点之间作出明确选择。运用排中律,就可以首先从逻辑上揭穿其诡辩手法,进而驳斥其观点的谬误。
人们不仅可以揭示对手的谬误,而且可以用排中律进行推理和论证,从正面阐述我们的观点。因为排中律是确认在同一思维过程中,两个互相矛盾或具有下反对关系的判断不能同假,必有一真,但到底哪个真不能确认,肯定有一个真的,也可能同真。所以,可以利用排中律进行推理和论证。
(三)运用排中律要注意以下几个问题
①若不是在“同一思维过程”的条件下,对两个互相否定的思想都加以否定,并不违反排中律。
②人们对于互相矛盾的判断,由于认识或客观实际的限制,暂时还不能分辩或回答,这种情况并不违反排中律。如,到底有没有UFO?现在既不肯定也不否定。这是大家都知道的事实。
③当某个复杂问语所隐含的判断不能成立或不能接受时,从而不用肯定或否定的方式来回答也不违反排中律。如有人问你“你现在还抽烟吗?”这句话中就隐含着另外一个判断,那就是“你以前抽烟”。无论你回答“是”或“不是”都得承认这个假定。这种问句,逻辑上称之为复杂问句。碰上一个复杂问句,当其中包含的那个假定是不能接受的时候,不要轻易回答,否则,就会陷入对方的圈套中。
④区分与矛盾律的不同。
其一是适用范围不同。矛盾律与排中律都针对两个互相矛盾的判断,但矛盾律还针对上反对关系;而排中律是对下反对关系的。
其二是内容不同。矛盾律指明“有假”,即指明两个互相矛盾或具有上反对关系的判断,不能同真,必有一假;而排中律是指明“有真”,即指明两个互相矛盾或具有下反对关系的判断,不能同假,必有一真。
其三是违反要求的错误不同。矛盾律不遵守规则导致的错误叫“模棱两可”;而排中律不遵守规则导致的错误叫“两不可”。
其四是实际作用不同。矛盾律是由真推假;而排中律是由假推真。
在了解了矛盾律与排中律的不同之后,就可以有条理地分析一个判断到底是适用矛盾律还是排中律,包括这个判断是否违反逻辑规律都是可以一目了然的。
首先,如果你遇到的两个判断具有上反对关系,那显然就要用矛盾律;如果是具有下反对关系的两个判断,就要用排中律。
其次,如果同时断定两个互相矛盾的概念或判断为真,则违反矛盾律;如果同时否定两个互相矛盾的概念或判断,则违反排中律。
总之,先看出现的是相互反对还是相互矛盾的概念或判断还是下反对关系的判断,再看对这些概念或判断是同时加以肯定,还是同时加以否定。这样就比较容易区分到底是违反了矛盾律还是排中律。
反证法(又称归谬法、背理法)是一种论证方式,他首先假设某命题不成立(即在原命题的条件下,结论不成立),然后推理出明显矛盾的结果,从而下结论说原假设不成立,原命题得证。
反证法常称作Reductio ad absurdum,是拉丁语中的“转化到不可能”,源自希腊语中的“ἡ εις το αδυνατον παγωγη”,阿基米德经常使用它。
“欧几里得最喜欢用的反证法,是数学家最精良的武器。它比起棋手所用的任何战术还要好:棋手可能需要牺牲一只兵或其他棋,但数学家用的却是整个游戏。”《一个数学家的辩解》,英国数学家高德菲·哈罗德·哈代。
维也纳的科学哲学家卡尔·波普尔的论点:“不能被反证的理论就不能被称作科学的理论”。(这里的反证不是指反证法,而是指推翻如证伪、修正、提出异议等。
反证法在数学中经常运用。当论题从正面不容易或不能得到证明时,就需要运用反证法,此即所谓"正难则反"。牛顿曾经说过:“反证法是数学家最精当的武器之一”。一般来讲,反证法常用来证明正面证明有困难,情况多或复杂,而逆否命题则比较浅显的题目,问题可能解决得十分干脆。应用反证法的是:欲证“若P则Q”为真命题,从相反结论出发,得出矛盾,从而原命题为真命题。
反证法是“间接证明法”一类,是从反方向证明的证明方法,即:肯定题设而否定结论,从而得出矛盾。法国数学家阿达玛(Hadamard)对反证法的实质作过概括:“若肯定定理的假设而否定其结论,就会导致矛盾”。具体地讲,反证法就是从反论题入手,把命题结论的否定当作条件,使之得到与条件相矛盾,肯定了命题的结论,从而使命题获得了证明。 在应用反证法证题时,一定要用到“反设”,否则就不是反证法。用反证法证题时,如果欲证明的命题的方面情况只有一种,那么只要将这种情况驳倒了就可以,这种反证法又叫“归谬法”;如果结论的方面情况有多种,那么必须将所有的反面情况一一驳倒,才能推断原结论成立,这种证法又叫“穷举法”。
原理1:给出命题P和命题(非P),根据排中律( ),两者之中起码有一个是真(更强的说法为,除了真和假之外并无其他的情况),所以若果其中一个是假的,另一个就必然是真。
),两者之中起码有一个是真(更强的说法为,除了真和假之外并无其他的情况),所以若果其中一个是假的,另一个就必然是真。
原理2:给出命题P和命题(非P),根据无矛盾律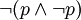 ,两者同时为真的情况
,两者同时为真的情况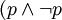 )为假。形式化为:
)为假。形式化为: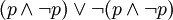 。与排中律的逻辑结构相同。
。与排中律的逻辑结构相同。
原理3:给出命题p和r,根据否定后件律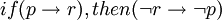 ,如果若成立p时出现r,则为r假时即为p假。
,如果若成立p时出现r,则为r假时即为p假。
反证法在要证明时,透过显示出若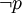 成立时出现矛盾,即为
成立时出现矛盾,即为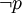 假,从而证明为P真。
假,从而证明为P真。
证明:命题P为真
详细论证以下命题为真:
A.沉默是金
B.和气生财
- 1.反命题为:话多是金。假设该命题为真。
- 2.举出实际反例:
a.言多必失,祸从口入。话过多,把自己底牌亮出,让自己处于信息不对称的地位,暴露自己的隐私与弱点,陷入被动的境地,极易破财。
b.话多误事,效率低下,浪费时间与精力,等同于破财。不节制说话的话,会忘记该做的事情。
c.话多容易造成重复啰嗦甚至伤害人,十分讨人厌,搞坏形象与人缘,等同于甚至甚于破财。一个只知道话多的人,他的思想是不会随着话多而增加的。
d.即使是有些靠说话谋生的人,也不能话多。如,主持人,销售员等,主要靠提问引导对方多说话而不是自己多说话。
e.话多不如话少,话少不如话精。人的内心是很隐密的,恭维了某个人可能就得罪了另一个人。 说话是门艺术,除了十分用脑,还要十分用心。心直口快,小事冒烟,大事冒火,是十分不用脑,十分不用心的表现,也是还没学会自我控制的表现,最终吃亏的就是自己。
f. 实证分析一下:冷静想想身边熟悉的人。话多财多,话多破财,闷声发财,闷声破财。从人数和财富的数量上,对比这四种人中,有没有典型代表,结论自然就能得出。
- 3.反命题:话多是金。该命题不成立。
- 4.据排中律:沉默是金。
- 5.和气生财,大致同理。
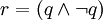 。据
。据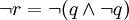








排中律,实质就是2选1。是排除法的特例。排除法是多选1。