拉格朗日乘數
出自 MBA智库百科(https://wiki.mbalib.com/)
拉格朗日乘數(Lagrange Multipliers)
目錄 |
在數學最優化問題中,拉格朗日乘數法(以數學家約瑟夫•拉格朗日命名)是一種尋找變數受一個或多個條件所限制的多元函數的極值的方法。這種方法將一個有n 個變數與k 個約束條件的最優化問題轉換為一個有n + k個變數的方程組的極值問題,其變數不受任何約束。這種方法引入了一種新的標量未知數,即拉格朗日乘數:約束方程的梯度(gradient)的線性組合里每個向量的繫數。
簡單舉例:
最大化 f(x,y)。
受限於 g(x,y) = c。
引入新變數拉格朗日乘數λ,即可求解下列拉格朗日方程
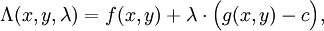
此方法的證明牽涉到偏微分,全微分或鏈法,從而找到能讓設出的隱函數的微分為零的未知數的值。
微積分中最常見的問題之一是求一個函數的極大極小值(極值)。但是很多時候找到極值函數的顯式表達是很困難的,特別是當函數有先決條件或約束時。拉格朗日乘數則提供了一個非常便利方法來解決這類問題,而避開顯式地引入約束和求解外部變數。
先看一個二維的例子:假設有函數:f(x,y),要求其極值(最大值/最小值),且滿足條件: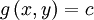 。
。
c 為常數。對不同dn的值,不難想象出 的等高線。而方程g的可行集所構成的線正好是g(x,y) = c。想象我們沿著g = c的可行集走;因為大部分情況下f的等高線和g的可行集線不會重合,但在有解的情況下,這兩條線會相交。想象此時我們移動g = c上的點,因為f是連續的方程,我們因此能走到
的等高線。而方程g的可行集所構成的線正好是g(x,y) = c。想象我們沿著g = c的可行集走;因為大部分情況下f的等高線和g的可行集線不會重合,但在有解的情況下,這兩條線會相交。想象此時我們移動g = c上的點,因為f是連續的方程,我們因此能走到 更高或更低的等高線上,也就是說dn可以變大或變小。只有當g = c和
更高或更低的等高線上,也就是說dn可以變大或變小。只有當g = c和 相切,也就是說,此時,我們正同時沿著g = c和
相切,也就是說,此時,我們正同時沿著g = c和 走。這種情況下,會出現極值或鞍點。
走。這種情況下,會出現極值或鞍點。
氣象圖中就很常出現這樣的例子,當溫度和氣壓兩列等高線同時出現的時候,切點就意味著約束極值的存在。
用向量的形式來表達的話,我們說相切的性質在此意味著f和g的切線在某點上平行。此時引入一個未知標量λ,並求解:
![\nabla \Big[f \left(x, y \right) + \lambda \left(g \left(x, y \right) - c \right) \Big] = 0](/w/images/math/4/0/6/406f930f4470f6f4e060122ab562d343.png)
且λ ≠ 0。
一旦求出λ的值,將其套入下式,易求在無約束極值和極值所對應的點。
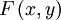 =
= 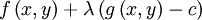
新方程F(x,y)在達到極值時與f(x,y)相等,因為F(x,y)達到極值時g(x,y) − c總等於零。
如f定義為在Rn上的方程,約束為gk(x)= ck(或將約束左移得到gk(x) − ck = 0)。定義拉格朗日Λ為
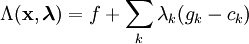 。
。
註意極值的條件和約束現在就都被記錄到一個式子里了:
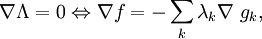 和
和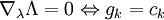 。
。
拉格朗日乘數常被用作表達最大增長值。原因是從式子: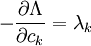 。中我們可以看出λk是當方程在被約束條件下,能夠達到的最大增長率。拉格朗日力學就使用到這個原理。
。中我們可以看出λk是當方程在被約束條件下,能夠達到的最大增長率。拉格朗日力學就使用到這個原理。
拉格朗日乘數法在Karush-Kuhn-Tucker最優化條件被推廣。
求此方程的最小值:
f(x,y) = x2y
同時未知數滿足
x2 + y2 = 1
因為只有一個未知數的限制條件,我們只需要用一個乘數λ。
g(x,y) = x2 + y2 − 1
Φ(x,y,λ) = f(x,y) + λg(x,y) = x2y + λ(x2 + y2 − 1)
將所有Φ方程的偏微分設為零,得到一個方程組,最大值是以下方程組的解中的一個:
2xy + 2λx = 0
x2 + 2λy = 0
x2 + y2 − 1 = 0
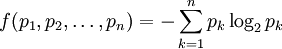 。
。
所有概率的總和是1,因此我們得到的約束是g(p)= 1即
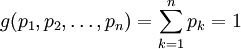 。
。
可以使用拉格朗日乘數找到最高熵(概率的函數)。對於所有的k 從1到n,要求

由此得到
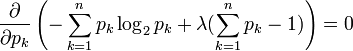 。
。
計算出這n個等式的微分,我們得到:
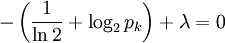 。
。
這說明pi都相等 (因為它們都只是λ的函數)。
解出約束∑k pk = 1,得到
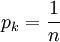 。
。
因此,使用均勻分佈可得到最大熵的值。
約束最優化在經濟學占有很重要的地位。例如一個消費者的選擇問題可以被視為一個求效用|效用方程在預算約束下的最大值問題。拉格朗日乘數在經濟學中被解釋為影子價格,設定在某種約束下,在這裡即收入的邊際效用。
拉格朗日乘數就是效用函數在最優解出對收入的偏導數,也就是在最優解處增加一個單位收入帶來的效用增加,或者說在最優解處有效用衡量收入的價值,稱之為收入的邊際效用。
在企業生產問題中,拉格朗日乘數用來衡量要素投入變動所帶來的收入變動,du/dm=λ,u表示效用函數或生產函數,m表示收入或要素投入。
在具體數學推導中還可以運用包絡定理的內容。







