弗里德曼的貨幣需求理論
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
美國經濟學家弗里德曼認為貨幣數量論並不是關於產量、貨幣收入或物價水平的理論,而是貨幣需求的理論,即貨幣需求是由何種因素決定的理論。因此,弗里德曼對貨幣數量論的重新表述就是從貨幣需求入手的。
弗里德曼將貨幣看作是資產的一種形式,用消費者的需求和選擇理論來分析人們對貨幣的需求。消費選擇理論認為,消費者在選擇消費品時,須考慮三類因素:收入,這構成預算約束;商品價格以及替代品和互補品的價格;消費者的偏好。
1、同理,影響人們貨幣需求的第一類因數是預算約束,也就是說,個人所能夠持有的貨幣以其總財富量為限。並以恆久收入作為總財富的代表。恆久收入是指過去、現在和將來的收入的平均數,即長期收入的平均數。弗里德曼註意到在總財富中有人力財富和非人力財富。人力財富是指個人獲得收入的能力,非人力財富即物質財富。弗里德曼將非人力財富占總財富的比率作為影響人們貨幣需求的一個重要變數。
2、影響貨幣需求的第二類因數是貨幣及其他資產的預期收益率,包括貨幣的預期收益率、債券的預期收益率、股票的預期收益率、預期物價變動率。
3、影響貨幣需求的第三類因數是財富持有者的偏好。
將貨幣視同各種資產中的一種,通過對影響貨幣需求7種因素的分析,提出了貨幣需求函數公式。貨幣學派強調貨幣需求與恆久收入和各種非貨幣性資產的預期回報率等因素之間存在著函數關係,貨幣需求函數具有穩定性的特點。
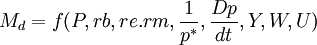
他認為:
他強調恆久性收入的波動幅度比現期收入小得多,且貨幣流通速度也相對穩定,所以貨幣需求也比較穩定。
弗理德曼認為,貨幣需求函數具有穩定性,理由是:
1、影響貨幣供給和貨幣需求的因素相互獨立。
2、在函數式的變數中,有些自身就具有相對的穩定性。
3、貨幣流通速度是一個穩定的函數。
因此,貨幣對於總體經濟的影響主要來自於貨幣的供應方面。
弗里德曼貨幣需求理論函數的前提假設[1]
由於1929~1933年的世界性經濟危機、二次世界大戰及戰後歐洲復興等事件先後發生,世界經濟長時期蕭條,因此,從1936年至20世紀50年代末,是“蕭條經濟學”――凱恩斯學派的全盛時期。但在這之後,大規模經濟蕭條現象已經不是世界經濟的主題,取而代之的是通貨膨脹問題。到70年代,簡單的通貨膨脹又變成了更為複雜的“滯脹”。這種經濟環境大前提的變化,導致了貨幣數量說的復興。 弗里德曼的前提假設與凱恩斯的假設在以下兩個方面存在差異:
1.長期分析,價格起作用,而且對未來的價格預期也起作用
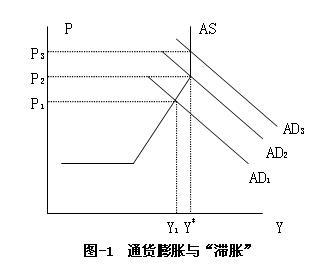
隨著歐洲經濟的恢復,世界經濟有了較大幅度的增長,如圖2-10,產出量(Y1)接近或達到了充分就業的產量Y * 。如果仍然按照凱恩斯經濟學指導下的財政政策和貨幣政策行事,則必然有總需求的進一步攀升(從AD1到AD3),其結果只能是“滯脹”――只有價格上漲,沒有經濟增長(價格從P2到P3)。在長期中,價格變數是變動的,對國民收入是有影響的。在通貨膨脹條件下(價格從P1到P2),價格或多或少會影響實際國民收入(從Y1到Y * );在“滯脹”條件下,價格影響名義國民收入。
60年代以來發生的持續通貨膨脹,不能不對人們關於下一期的價格預測發生影響。價格預期一定有三種情形:看漲、看跌和不變,前兩者都會對人們的支出產生影響,從而對經濟發生作用。正如許多經濟學家所說,“大多數人預期什麼,就會發生什麼”。
2. 貨幣量的層次為 ,即包括貨幣和準貨幣
與凱恩斯不同,弗里德曼擴大了貨幣的涵蓋內容,將貨幣定義在了廣義貨幣層次上,即業內人士所說的 。眾所周知,貨幣的定義有許多種,譬如,美聯儲對貨幣的定義就不下6種。多數經濟學家是從純理論角度,即貨幣的功能方面來討論貨幣定義的。而貨幣學派則不同,弗里德曼認為貨幣定義應以嚴格的計量經濟學方法來測定。確定最適當的貨幣定義的標準是:
(1)貨幣總量與國民收入的相關係數最大。如,M2與GDP的相關係數若分別大於M1、M3與GDP的相關係數,則M2作為貨幣的可能性較大。同時,還要看第二個標準。
(2)貨幣總量與國民收入的相關係數要分別大於總量中各個組成部分與國民收入的相關係數。如,M2與GDP的相關係數要大於M0(現金)、Dd(活期存款)、Dt(定期存款)與GDP的相關係數。
上述兩個標準必須同時滿足。弗里德曼和安娜·雅各布森·施瓦茨(Anna Jacobson Schwartz,1915—)就是根據這兩個標準確定M2是最佳貨幣定義的。
弗里德曼貨幣需求理論函數[1]
1956年,弗里德曼發表了著名論文《貨幣數量說的重新表述》。在文中,弗里德曼將貨幣需求理論函數表述如下:
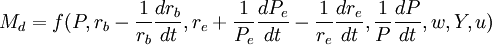 (1)
(1)
式(1)中的符號意義、函數與自變數的相關關係如下:
1、Md為名義貨幣需求,它是因變數,是受自變數決定的。
2、P為價格指數,為了實現正常消費或經營,商品和服務的價格越高,所需貨幣量就應該越多,二者正相關。
3、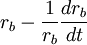 為債券的預期名義收益率;其中,rb為債券利率。比較費解的分式
為債券的預期名義收益率;其中,rb為債券利率。比較費解的分式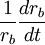 是債券利率的預期變動率。為什麼寫成這種形式呢?我們對此做一簡單的解釋。經驗指出,債券利率隨時間的變化而變化,即rb = f(t)。若求函數在任一點上的變化率,則要對函數求對數的導數(lnrb)t。根據複合函數的求導法則,有
是債券利率的預期變動率。為什麼寫成這種形式呢?我們對此做一簡單的解釋。經驗指出,債券利率隨時間的變化而變化,即rb = f(t)。若求函數在任一點上的變化率,則要對函數求對數的導數(lnrb)t。根據複合函數的求導法則,有
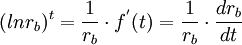 (2)
(2)
弄清了數學表達式的意義之後,再來討論一下變數與函數的相關關係。當期債券利率減去債券利率的預期變動率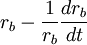 ,就是債券的預期收益率。債券的預期收益率上升,意味著持有貨幣的機會成本加大,理性的經濟個體必然要儘可能地減少貨幣需求量,用有較大預期收益的債券替代。反之則反是。顯然,債券的預期收益率與貨幣需求量負相關。
,就是債券的預期收益率。債券的預期收益率上升,意味著持有貨幣的機會成本加大,理性的經濟個體必然要儘可能地減少貨幣需求量,用有較大預期收益的債券替代。反之則反是。顯然,債券的預期收益率與貨幣需求量負相關。
4.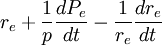 為股票的預期名義收益率;其中,re為股票收益率;
為股票的預期名義收益率;其中,re為股票收益率;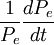 為預期資本損益率,即股票價格變化率,數學意義同前; 為股票收益率的預期變化率。
為預期資本損益率,即股票價格變化率,數學意義同前; 為股票收益率的預期變化率。
股票的預期名義收益率的機理與債券相同,變數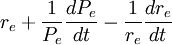 與函數Md也是負相關的。
與函數Md也是負相關的。
5. 與前面的道理相同,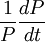 為預期價格變動率。如果預期物價上升,就意味著下一期貨幣的購買力將降低。於是,人們勢必會減少貨幣持有量,以其它能保值的資產保值。反之則反是。Needless to say,二者是負相關的。
為預期價格變動率。如果預期物價上升,就意味著下一期貨幣的購買力將降低。於是,人們勢必會減少貨幣持有量,以其它能保值的資產保值。反之則反是。Needless to say,二者是負相關的。
6. w為人力財富在總財富中的比例,按弗里德曼的思路可以用下式來表示:
|
|
在弗里德曼的貨幣需求理論函數中, 與 是什麼關係?不知道為什麼,弗里德曼沒有說明。而且,在貨幣理論界,對此也無普遍接受的研究結論。
7.Y為“恆久收入”。恆久收入不同於我們經常使用的“統計收入”概念,它是統計收入與“臨時收入”的代數和,換言之,恆久收入的統計量是統計收入的幾何加權平均值。弗里德曼為什麼用恆久收入替代一般的國民收入呢?我們的理解是這樣的:在長期中,假定一個人的平均收入水平是月薪6000元,他就基本上形成了一個較為穩定的消費支出習慣,因而決定了貨幣需求量。他不會因某一個月收入偶然的提高或降低而改變自己的消費支出習慣,從而貨幣需求量。譬如,增加了1000元,他可能用其購買公債;減少1000元,他可能賣出一部分手中的公債,以保證消費支付習慣不變。如果他確信平均收入從此就提高(降低)到了某一新的水平上,他將調整自己的消費支出習慣,從而決定新的貨幣需求量。這裡所說的“平均收入”,大致就是“恆久收入”的含義。
恆久收入與Md的相關關係如同凱恩斯的收入與Md一樣,是正數相關的。
8.u為影響持有貨幣效用的其它隨機因素,如偏好、與貨幣有關的制度變化等等。顯然,由於u的隨機性,它與Md的關係不定。
需要說明,在許多經濟學專著中,變數與函數的關係都是用一階偏導數來表示的。我們知道,導數是函數在某一點上的變化率,是曲線上該點切線的斜率。這個斜率大於0時,自變數與函數同升同降,正數相關;反之,斜率小於0,自變數與函數反向變動,負數相關。
後來,在《美國和英國的貨幣趨勢》一書中,弗里德曼將單個財富持有者的貨幣需求理論函數簡化為:
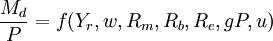 (3)
(3)
式(3)中符號的意義如下:
1.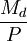 為實際貨幣需求;
為實際貨幣需求;
2. Yr為實際恆久收入,即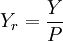 ;
;
3. w、u的意義同式(1);
3. Rm為貨幣的預期名義收益率,在其它條件不變時,可以理解為定期存款的預期收益率。這是個新出現的變數,因為它是度量持有貨幣收益的,所以,它與貨幣需求之間應該是正相關的。
4. Rb相當於式(1)的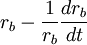 ;
;
5.re相當於式(1)的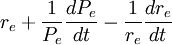 ;
;
6. gP相當於式(1)的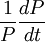 。
。
除了用簡單的符號代替了式(1)中的某些艱澀的數學表達式、加入了貨幣收益率變數之外,式(3)與式(1)的顯著區別是,函數用實際貨幣需求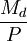 取代了名義貨幣需求Md。這是怎麼轉換的呢?換句話說,價格變數 是怎麼跑到等式的左端去的呢?
取代了名義貨幣需求Md。這是怎麼轉換的呢?換句話說,價格變數 是怎麼跑到等式的左端去的呢?
弗里德曼進一步假定,函數由實際變數決定,即與衡量貨幣變數的名義單位完全獨立。如果衡量物價、名義收入的單位發生變化,則貨幣需求也作同比例變化。用數學語言描述,即式(1)對 和 是一階齊次的。回顧一下我們學過的高等數學:
若某一函數的自變數乘以常數λ,該函數值以λn的倍數發生變化,則該函數稱為n階齊次函數。設,函數f(x,y),若f(\lambda x,\lambda y)=\lambda f(x,y),則該函數對x、y為一階齊次。
這樣,式(1)可以寫成:
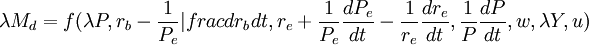
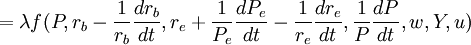 (4)
(4)
令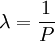 ,代入式(4)則有
,代入式(4)則有
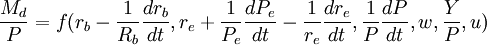 (5)
(5)
按式(3)的符號簡化、加入貨幣預期收益率,即
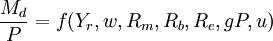
在式(1)的基礎上(為方便起見,將符號簡化),弗里德曼進一步假定: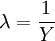 ,則有
,則有
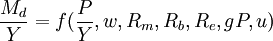 (6)
(6)
移項,得
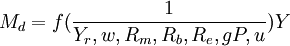 (7)
(7)
令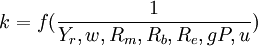 ,將名義收入寫成PYr,代入式(7),得
,將名義收入寫成PYr,代入式(7),得
Md = kPYr 或 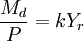
貨幣供給與貨幣需求事後相等,可以去掉貨幣需求符號的下標
M = kPYr 或 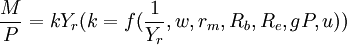 (8)
(8)
令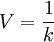 ,代入式(8),則有
,代入式(8),則有
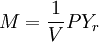
MV = PYr(9)
式(8)簡直就是劍橋學派的貨幣數量方程式!式(9)與交易方程式幾無二致!不過,弗里德曼“新貨幣數量論”的持幣率 k 或貨幣流通速度 V 已不再是常數,而是一個比較複雜的函數。從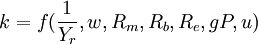 可以看出 k、V 與各變數之間的相關關係。
弗里德曼的貨幣需求理論函數雖然在形式上反映了凱恩斯的影響,但函數的內容則比凱恩斯的流動性偏好理論精密。就貨幣需求函數的一般形式(1)、(3)兩式而言,基本上被學術界接受,沒有什麼爭論了。但是,弗里德曼運用齊次公式,將貨幣需求函數轉換為式(8)或(9),無疑是對古典貨幣數量說的重建。同時,弗里德曼認為,新貨幣數量論的 或 雖與劍橋方程式的 及費雪交易方程式的 之常數推論有別,但它們基本上是穩定的、可測的函數,甚至“比消費函數或其它主要函數更為穩定”。
可以看出 k、V 與各變數之間的相關關係。
弗里德曼的貨幣需求理論函數雖然在形式上反映了凱恩斯的影響,但函數的內容則比凱恩斯的流動性偏好理論精密。就貨幣需求函數的一般形式(1)、(3)兩式而言,基本上被學術界接受,沒有什麼爭論了。但是,弗里德曼運用齊次公式,將貨幣需求函數轉換為式(8)或(9),無疑是對古典貨幣數量說的重建。同時,弗里德曼認為,新貨幣數量論的 或 雖與劍橋方程式的 及費雪交易方程式的 之常數推論有別,但它們基本上是穩定的、可測的函數,甚至“比消費函數或其它主要函數更為穩定”。
在《1867~1960年美國貨幣史》一書中,弗里德曼做出了實證研究結論:在將近100年的時段上,美國貨幣流通速度大致以每年1%的速度減慢。將大時段拆分的情況是:1880~1914年,貨幣流通速度從4.97下降到1.91;1914~1929年,貨幣流通速度無明顯變動;1929~1946年,貨幣流通速度有所下降;1946年以後開始回升,但仍低於1920年的水平,也低於1914年的水平。
對於V每年遞減1%的問題,弗里德曼受到了同行激烈的挑戰。後來,弗里德曼本人也承認這一結論是有問題的。經濟學大師的這種求是的科學態度,是值得我們後輩學習的。
貨幣需求理論函數的簡化[1]
弗里德曼的貨幣需求理論函數包括的變數多、形式複雜,可以在無損主旨的情況下加以簡化。我們從式(3)開始:
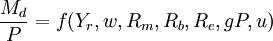 (3)
(3)
1、假定u穩定。因為,與貨幣相關的制度通常是比較穩定的,偏好、習慣等因素也不會輕易改變,所以,可以視為一個常量從函數中略去。於是有:
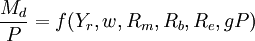 (10)
(10)
2、由於財富的構成比例 在一定時期內也是比較穩定的,它對貨幣需求的影響不會有顯著的變化,所以也可以從函數中刪除。於是有:
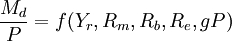 (11)
(11)
3、根據一些國家的統計數據,只有當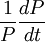 (或寫作gP)變動幅度很大、持續時間很長時,才會對貨幣需求量產生顯著影響。經驗指出,這種情況很少發生。因此,
(或寫作gP)變動幅度很大、持續時間很長時,才會對貨幣需求量產生顯著影響。經驗指出,這種情況很少發生。因此,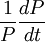 也可以略去。於是有:
也可以略去。於是有:
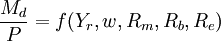 (12)
(12)
4、一般情況下,狹義的貨幣收益率Rm僅指定期存款Dt的利率,這個利率通常也不高。如果將定期存款Dt所獲利息除以M2(M0 + Dd + Dt),計算出的利率應該是相當低的。況且,銀行利率的變動一般又是相當緩慢的。因此,該變數對貨幣需求的影響應該是極不顯著的,可以略去。於是有:
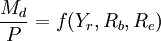 (13)
(13)
5、兩種金融資產的收益率Rb、Re是受大致相同的因素決定二者高度正相關,用一個收益率作變數,完全可以替代和反映出另一個收益率的變動。因此,可以將二者合併,不妨以“市場利率”統稱之。若市場利率仍用 表示,則有:
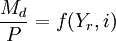 (14)
(14)
式(14)即為弗里德曼貨幣需求理論函數的最終簡化式。
對貨幣需求理論函數的實證[1]
實證研究要做的工作是,確定函數中各個獨立變數的作用。具體說,貨幣需求對利率的彈性如何?貨幣需求對收入或財富變動的敏感性如何?貨幣需求對其它列入貨幣需求函數或未列入貨幣需求函數的變數的依存程度如何?等等。此外,還有一個基本概念的問題,即貨幣是什麼?究竟採用哪個層次上的貨幣量較為適宜?
除了構造科學的模型和運用正確的計量方法之外,實證研究的先決條件是,能夠獲得可靠的統計數據。事實上,若無統計數據,實證研究就根本無法進行。因此,實證研究的數據多得自於統計工作比較完備的美國、西歐和日本。
根據貨幣需求理論函數的簡化式(14),實際貨幣需求是由實際收入和市場利率兩個因素決定的。但是,式(14)僅是一般函數形式,需要將其以某種方程形式表示出來。弗里德曼及其貨幣學派在大量的實證分析中摸索建立瞭如下方程:
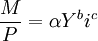 (15)
(15)
式(15)是一個冪函數曲線的回歸方程,a,b,c是由回歸分析決定的參數。用回歸分析方法檢驗非線性方程有一定困難,可以用對數方法把非線性方程化為線性方程:
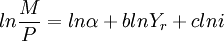 (16)
(16)
式(16)是一個二元回歸方程,被認為是“近年來貨幣數量論者通過大量的對貨幣需求的經驗研究所得出的基本公式”。回歸繫數可用最小二乘法求得。貨幣學派根據美國1892~1960年的統計數據計算出:
ln a=3.003 b=1.394 c=-0.155 R2 = 0.99
將上述回歸繫數寫入方程,有
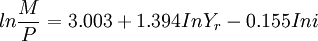 (17)
(17)
式(17)中,M為廣義貨幣M2,Yr為實際恆久收入,i為4—6個月商業票據利率。式(17)表明, Yr與 i 的變動可以高度解釋(擬合優度R2 = 0.99)M的變動,且實際貨幣需求的收入彈性為1.394。收入彈性說明,當實際收入提高1%時,實際貨幣需求將提高1.394%。反之則反是。同時,式(17)還說明,實際貨幣需求的利率彈性為-0.155,即當利率提高1%時,實際貨幣需求下降0.155%,幾乎無彈性。
不過,對於貨幣需求的收入彈性結論,弗里德曼自己也多有修正。
1959年,他認為是1.8;
1970年,他認為是1.0~2.0,並將其分為1.0~1.5和1.5~2.0兩段。
無庸諱言,在實證方面,許多學者與弗里德曼及其貨幣學派有分歧。
弗里德曼對貨幣需求理論的貢獻[1]
1、將貨幣視為一種資產,從而將貨幣理論納入了資產組合選擇理論的框架,摒棄了古典學派視貨幣為純交易工具的狹隘理念。
2、在一般均衡的資產組合理論中,特別強調貨幣量在經濟中的樞紐作用,糾正了凱恩斯學派忽視貨幣量的偏頗
3、在貨幣需求函數中,首先設置了預期物價變動率這一獨立變數,確定了預期因素在貨幣理論中的地位
4、嚴格地將名義量和實際量加以區分。
5、特別強調實證研究的重要性,改正了以往學者們在經濟理論,尤其是在貨幣理論中只顧抽象演繹的缺陷,使貨幣理論更向可操作的貨幣政策靠攏了。
弗里德曼的貨幣需求理論與凱恩斯的貨幣需求理論的區別 [2]
1、在凱恩斯的貨幣需求函數中,利率僅限於債券利率,收入為即期的實際收入水平。而在弗里德曼的貨幣需求函數中,利率則包括各種財富的收益率,收入則是具有高度穩定性的恆久收入,是決定貨幣需求的主要因素。
2、凱恩斯的貨幣需求函數是以利率的流動性偏好為基礎的,認為利率是決定貨幣需求的重要因素。而弗里德曼則認為,貨幣需求的利率彈性較低,即對利率不敏感。
3、凱恩斯認為,貨幣流通速度與貨幣需求函數不穩定。而弗里德曼則認為,貨幣流通速度與貨幣需求函數高度穩定。
4、凱恩斯認為,國民收入是由有效需求決定的,貨幣供給量對國民收入的影響是一個間接作用的過程,即經由利率、投資及投資乘數作用而作用於社會總需求和國民收入。弗里德曼則認為,由於貨幣流通速度是穩定的,貨幣流通速度的變動則直接引起名義國民收入和物價水平的變動,所以貨幣是決定總支出的主要因素。
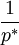 預期物價變動率;
預期物價變動率;








謝謝