巨集觀模擬模型

出自 MBA智库百科(https://wiki.mbalib.com/)

　　巨集觀模擬模型是直接將信用等級轉換概率與巨集觀因素之間的關係模型化，並且，如果模型是擬合的，就可以通過製造巨集觀上的對於模型的“衝擊”來模擬信用等級轉換概率的跨時期演變狀況。

　　1)盯市模型或違約模型

　　根據模型對信用損失的不同定義，可以將模型分為兩類：以貸款的市場價值變化為基礎計算的風險價值模型稱為盯市模型(Marked-to-Market Model)，集中於預測違約損失的風險價值模型稱為違約模型(Default Model)。盯市模型在計算貸款價值的損失和收益中既考慮了違約因素，同時又考慮了貸款信用等級上升或下降以及由此而發生的信用價差變化等因素。違約模型只考慮了兩種狀態，即違約或不違約。盯市模型和違約模型之間的關鍵差異是盯市模型包括了價差風險。常見的四種風險計量模型中信用度量術模型明顯是一種盯市模型，Credit Risk+模型和KMV模型則本質上是違約模型，而信用組合觀點既可以被當做盯市模型使用，又可以被當做違約模型使用。

　　2)信用風險驅動因素

　　信用組合觀點的風險驅動因素有著與信用度量術和KMV方法的風險驅動因素在本源上的相似之處。特別是，一套系統的“國家範圍的”巨集觀因素和非系統的巨集觀衝擊驅動著違約風險和借款人之間違約風險的相關性。

　　信用度量術方法和KMV方法以默頓模型為分析基礎，企業的資產價值和資產價值的波動性是違約風險的關鍵性驅動因素。在信用組合觀點中，信用風險驅動因素是一些巨集觀因素。

　　3)信用事件的波動性

　　在信用組合觀點中，違約概率是一套呈正態分佈的巨集觀因素和衝擊的一個對數函數，因此，隨著巨集觀經濟的演變，違約概率以及信用等級轉換矩陣中其餘的單元或概率也會變化。

　　4)模型的數字方法

　　信用組合觀點方法使用重覆的蒙特卡羅模擬法來生成巨集觀的衝擊和貸款組合損失或貸款價值的分佈，從而最終也能算出風險價值。

　　1)周期性因素的處理

　　(1)將過去的樣本區間劃分為衰退期和非衰退期，並且分別計算這兩個時期的信用轉移矩陣，以得到兩種不同的VaR結果。

　　(2)直接將信用轉移概率與巨集觀因素之間的關係模型化，並且如果模型是擬合的，就通過巨集觀因素對於模型的修正來模擬信用轉移概率的演變。這就是巨集觀模擬方法，麥肯錫公司的信用組合模型應用的就是這種方法。

　　2)巨集觀模擬方法

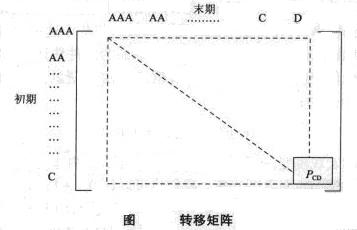
　　對於一個給定國家的信用狀況，可以利用轉移矩陣表述(見圖)。轉移矩陣的每一個單元顯示的是一個特定交易對手在初期被評為一定的信用級別而在期末移往另一個信用級別的概率。圖中估計的是一個被評為c級的借款人(投機級別的借款人)下一年會違約的概率，即它會從C級移往D(違約)的概率。

　　一般而言，人們可以預期這一概率在商業周期期間會變動較大，而在衰退期間的變動會比在擴張期間更高。令P_CD在時間t隨同一套巨集觀因素而變化，設這些巨集觀因素可以用變數y加以表示。模型中的C級借款人在下一個時期(如1年)里的違約概率以一般的形式表示為：

　　P_t = f(Y_t)　　(1)

　　式中：f<0，表示在經濟狀態與違約概率之間存在反向聯繫。反映巨集觀指標的變數Y_t可以被看做是由時間t在i種(系統的)巨集觀經濟變數的集合(X_it)以及(非系統的)隨機衝擊或經濟體系的創新(V_t)所共同推動的。一般的，有如下關係：

　　y_t = g(X_it,V_t)　　(2)

　　式中：i=1，…，n，並且V_it～N(0,σ)。

　　依次的，諸如國內生產總值(GDP)的增長、失業率以及其他巨集觀經濟變數(X_it)本身可以被視為由過去的歷史(比如滯後的GDP增長)決定，並且也對其自身受到的衝擊(ε_it)敏感。因而：

　　X_it = h(X_{it − 1},X_{it − 2},...,ε_it)　　(3)

　　可以將不同巨集觀模型的具體形式運用於式(2)和式(3)的環境中以改善模型的擬合性，也可以用不同的模型解釋不同國家和行業的轉移。

　　將式(3)代人式(2)，再將式(2)代入式(1)，就可以用下式確定一種投機性(C級)貸款在下一年內移往D級的概率：

　　P_t = f(X_{it − j};V_t,ε_it)　　(4)

　　式(4)建立了決定這一轉移概率的模型，認為它是滯後的巨集觀經濟變數(X_{it − j})一般性經濟衝擊因素或“創新”(V_t)以及每一個巨集觀變數i的衝擊因素或創新(ε_it)的函數。因為X_{it − j}是事先確定的，推動P_t的關鍵變數是創新或衝擊V_t和ε_it。使用蒙地卡羅模擬方法，可以產生未來多期的V_t和ε_it數值。我們可以在擬合的巨集觀模型中使用模擬而得的V值和\epsilon以模擬在未來時期t，t+1，t+2，…，t+n中P_CD的值。

　　假設基於當前的巨集觀形勢，以P ⁺ 表示P_CD的模擬值為0．35，即通過式(4)計算出來的違約概率值，在歷史上的無條件的轉移矩陣中這一數值為0．30。因為無條件的轉移概率值0．30小於以巨集觀經濟狀態為條件估計出的數值0．35，所以我們可能會低估貸款和貸款組合的VaR值，特別是在貸款低質量的情況下。

　　定義比率(r_t)為：

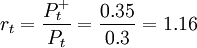　　　　(5)

　　基於模擬的巨集觀模型，一個C級的借款人在下一年內違約的概率要比歷史上的無條件的平均轉移概率高出16％。我們也可以計算t+1，t+2，以及再往後時期的這一比率。這些計算出來的比率可以被用來調整t，t+1，…，t+n期轉移矩陣圖中的元素。在信用組合觀點模型中，通過有條件的P_CD對其無條件的P_CD值加以調整：r_t×0．30=0．35。我們用0．35代替轉移矩陣里的0．30，這也意味著我們需要調整轉移矩陣中的所有其他元素(如P_CA等)。可以通過許多步驟做到這一點，包括轉移矩陣中的每一個元素或單位對於比率r_t的線性的和非線性的回歸。

　　對於每一年會有不同的轉移矩陣。這些調整後的矩陣反映出巨集觀經濟衝擊對於轉移概率的模擬的影響。我們也可將這種方法應用到信用度量術中以計算對於周期敏感的1年，2年，……，n年的VaR值。