容差設計
出自 MBA智库百科(https://wiki.mbalib.com/)
容差設計(Tolerance Design)
目錄 |
容差是從經濟角度考慮允許質量特性值的波動範圍。容差設計通過研究容差範圍與質量成本之間的關係,對質量和成本進行綜合平衡。容差設計在完成系統設計和由參數設計確定了可控因素的最佳水平組合後進行,此時各元件(參數)的質量等級較低,參數波動範圍較寬。
容差設計的目的是在參數設計階段確定的最佳條件的基礎上,確定各個參數合適的容差。
容差設計的基本思想如下:根據各參數的波動對產品質量特性貢獻(影響)的大小,從經濟性角度考慮有無必要對影響大的參數給予較小的容差(例如用較高質量等級的元件替代較低質量等級的元件)。這樣做,一方面可以進一步減少質量特性的波動,提高產品的穩定性,減少質量損失;另一方面,由於提高了元件的質量等級,使產品的成本有所提高。因此,容差設計階段既要考慮進一步減少在參數設計後產品仍存在的質量損失,又要考慮縮小一些元件的容差將會增加成本,要權衡兩者的利弊得失,採取最佳決策。
總之,通過容差設計來確定各參數的最合理的容差,使總損失(質量與成本之和)達到最佳(最小)。我們知道,使若幹參數的容差減少需要增加成本,但由此會提高質量,減少功能波動的損失。因此,要尋找使總損失最小的容差設計方案。用於容差設計的主要工具是質量損失函數和正交多項式回歸。
容差設計與參數設計的關係
參數設計與容差設計是相輔相成的。按照參數設計的原理,每一層次的產品(系統、子系統、設備、部件、零件),尤其交付顧客的最終產品都應儘可能減少質量波動,縮小容差,以提高產品質量,增強顧客滿意;但另一方面,每一層次產品均應具有很強的承受各種干擾(包括加工誤差)影響的能力,即應容許其下屬零部件有較大的容差範圍。對於下屬零部件通過容差設計確定科學合理的容差,作為生產製造階段符合性控制的依據。但應指出,此處的符合性控制與傳統質量管理的符合性控制有兩點不同:第一,檢驗工序不能只記錄通過或不通過,還應記錄質量特性的具體數值;不能只給出不合格率,還要按照質量損失的理論制訂科學的統計方法來給出質量水平的數據。第二,採用適應健壯設計的線上質量控制方法(如先進的SPC方法等),實時監控產品質量波動的情況,進行反饋和工藝參數的調整;針對存在的問題,不斷地採取措施改進工藝設計,提高產品質量,在減少總損失的前提下使質量特性越來越接近目標值,條件具備時,應減少容差範圍。
容差設計的實現途徑很多,比較常見的有極值分析法(WorstCase)、統計平方公差法(Root-Sum-Squares)和模擬法(Simulation)三類,下麵將會結合實際案例作各自的說明和相互的比較。在高端六西格瑪統計分析軟體JMP的協助下,容差設計的工作效率更加高速,分析結果更加清晰。在案例分析中,JMP軟體是目前唯一一款集統計分析功能和專業模擬功能於一身的六西格瑪統計分析軟體,也是目前全球試驗設計方法的領導品牌。
一、極值分析法(WorstCase)
極值分析法是目前應用範圍最廣泛、操作最簡便的方法,大多數的設計都基於這個概念。在這種方法中,零部件都設計為名義值,然後假定容差差完全向一個或另一個方向積累,最終的結果仍能滿足產品的功能要求。
在極值分析法分析中主要考慮的是設計規格的線性極值,它雖然確保了所有零件的組合,但往往導致最終結果過於保守,產生過大或過小的容差。而且嚴格地說,極值分析法並不屬於統計方法,但它為後面講到的統計平方公差法提供了比較的基礎,能夠幫助我們更好地意識到應用統計方法的好處。我們通過一個典型的機械繫統設計案例來加深理解。
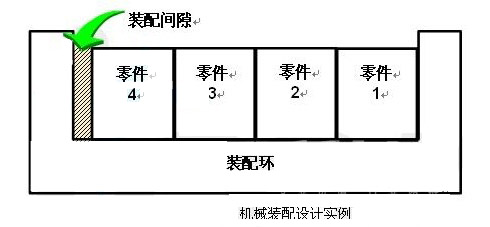
場景:在一個裝配環中裝入4個零件,如下圖所示,要求裝配間隙Gap的目標值T=0.016,波動範圍儘可能小。已知現在的零件1~4服從技術規範1.225±0.003,裝配環服從技術規範4.916±0.003。試問:該系統的的目標值是否達到要求?公差範圍是多少?
根據極值分析法的分析思路:
裝配環的名義值=4.916 公差=±0.003
零件1的名義值=-1.225 公差=±0.003
零件2的名義值=-1.225 公差=±0.003
零件3的名義值=-1.225 公差=±0.003
零件4的名義值=-1.225 公差=±0.003
由此我們可以得到:
間隙的名義值=0.016 總公差=±0.015
間隙的最小值=0.001
間隙的最大值=0.031
也就是說,系統的目標值達到了要求,系統的公差範圍是[0.001,0.031],然而實際情況果真如此嗎?系統中每個零部件出現極值的概率分別隻有0.0027,由此組成的系統(即間隙)出現極值的概率=0.00275=0.000000000000143,幾乎接近於0。這說明,通過極值分析法估算出來的公差範圍過大,沒有反應系統的真實情況。
二、統計平方公差法(Root-Sum-Squares)
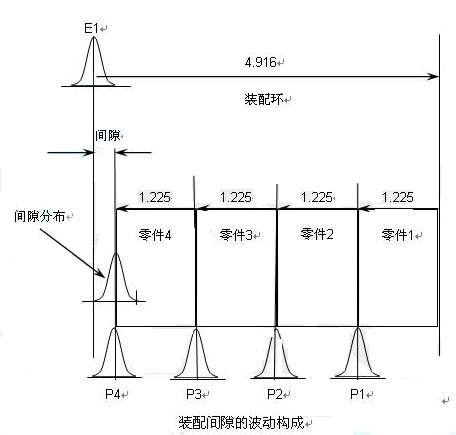
統計平方公差法基於這樣一個假設理論:大多數的零部件在它們的公差範圍內呈正態概率分佈,此時由它們所構成的系統與各個零部件線性相關,則系統的分佈也可以用一個正態分佈或近似正態的分佈來表示。結合上一個機械繫統的案例,這個理論可以用下圖表示。
統計平方公差法採用統計分析方法進行公差分析,防止了產生過於保守的設計,適當地擴展了零部件的允許公差,如果清楚過程能力,甚至可以得到更寬鬆的公差。
這時候,在同一個機械繫統的狀況下,根據統計平方公差法的定義公式,間隙的總公差=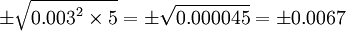
間隙的最小值=0.016-0.0067=0.0093
間隙的最大值=0.016+0.0067=0.0227
也就是說,系統的公差範圍變為[0.0093,0.0227],相對於極值分析法的結論,它顯得更加接近現實情況。但是,統計平方公差法也存在一個先天性的缺陷:當初始的假定理論不成立,即零部件明顯不呈正態概率分佈,或者系統與各個零部件呈非線性相關時,原先統計平方公差的計算公式也就不成立了。
三、模擬法(Simulation)
模擬也稱模擬,是指通過設定若幹個隨機變數以及相互之間的關係建立系統的數學模型或邏輯模型,並對該模型進行充分的試驗,以獲得對該系統行為的認識或者幫助解決決策問題的過程。自上世紀八十年代起,隨著電子電腦軟硬體的普及,模擬得到了廣泛應用,它的操作也越來越簡單。
在容差設計時應用模擬技術,分析人員無需組建真實的系統就能夠評價模型,或者在不幹擾現有系統的情況下對模型進行驗證。而且模擬法對零部件的分佈和模型的線性性要求較低,比許多其他的分析方法更容易被人理解。
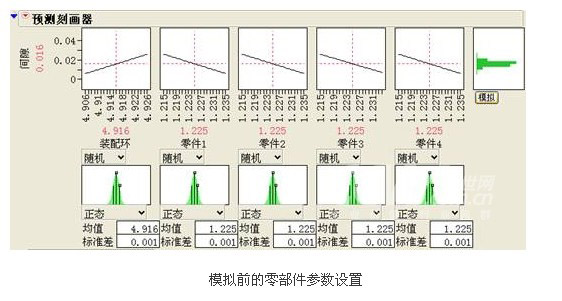
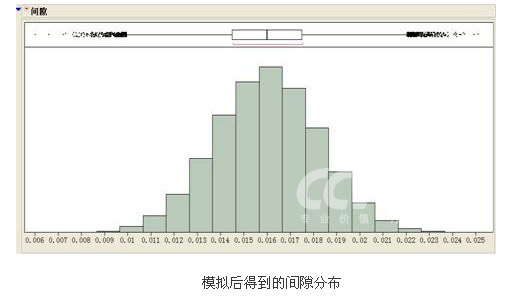
再次借用機械繫統的案例,我們首先在高級DOE分析軟體JMP里對裝配過程中的各個零部件參數進行設置,一般認為參數服從正態分佈,均值等於中心值,標準差為半公差的1/3(具體操作參見上圖)。短短幾秒鐘後,彙總十萬次模擬結果的間隙分佈就由JMP軟體自動生成了。從下圖可以看到,通過模擬法得到的系統的公差範圍變為[0.009,0.023],與統計平方公差法的結論十分相似,非常接近現實情況。同時,模擬法的分析過程生動形象,由它獲取的結果的可讀性依然很強。更重要的是,當遇到電子線路等非線性模型時,統計平方公差法已不適用,但模擬法卻依然有效。
以上花了很多篇幅介紹瞭如何正確地預測系統的公差範圍。一旦發現系統的公差範圍過大時,應該怎樣調整零部件參數的公差設置呢?正如我們所知道的,減少零部件參數的公差會提高質量,減少系統功能波動的損失,但缺憾是往往需要增加成本。通過公差設計,可以確定各參數的最合理公差,使總損失(質量損失與材料成本之和)達到最佳(最小)。接下來將用最簡單易懂的模擬法來簡要說明。
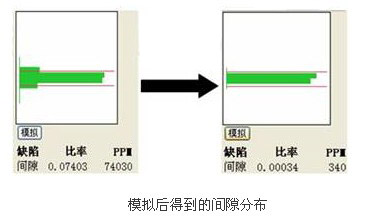
例如,設定在上述的機械繫統中顧客滿意的間隙波動範圍為[0.012,0.020],顯然會有相當一部分產品被判為不合格。如果將各個零部件參數的公差都縮小一半,效果是否會明顯改善呢?在高級統計分析軟體JMP自帶的模擬器的幫助下,我們很快會得到如下圖所示的缺陷前後對比。間隙地缺陷數量從原先的74030PPM迅速下降到改進後的340PPM,充分說明效果是明顯的。如果能夠證明因此改進而增加的成本不高時,那我們就更有信心將零件1-4的公差範圍設定為1.225±0.0015,裝配環的公差範圍設定為4.916±0.0015。








瞭解下概念。