符號檢驗
出自 MBA智库百科(https://wiki.mbalib.com/)
符號檢驗(Sign test)
目錄 |
符號檢驗法是通過兩個相關樣本的每對數據之差的符號進行檢驗,從而比較兩個樣本的顯著性。具體地講,若兩個樣本差異不顯著,正差值與負差值的個數應大致各占一半。
符號檢驗與參數檢驗中相關樣本顯著性t檢驗相對應,當資料不滿足參數檢驗條件時,可採用此法來檢驗兩相關樣本的差異顯著性。
根據符號檢驗判斷差異顯著性時也要查表找出相應的臨界值。但特別應註意的是在某一顯著性水平下,實得的r值大於表中r的臨界值時,表示差異不顯著,這一點與參數檢驗時的統計量和臨界值的判斷結果不同。
表1 單側符號檢驗統計判斷規則
| r與臨界值的比較 | P值 | 顯著性 |
| r > r0.05 | P>0.05 | 不顯著 |
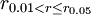 | 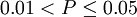 | 顯著 |
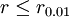 | 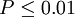 | 極顯著 |
編符號:一對一比較,如果前者大於後者,或者前者較優,記以符號”+”,否則記以”-”,如二者相等或不能判明優劣,就記為”0”。 建立假設:
H0:P(X1 > X2) = P(X2 > X1) = 0.5
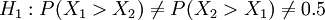
清點“+”、“-”、“0”各有幾個,分別記為n+、n-、n0
進行顯著性檢驗
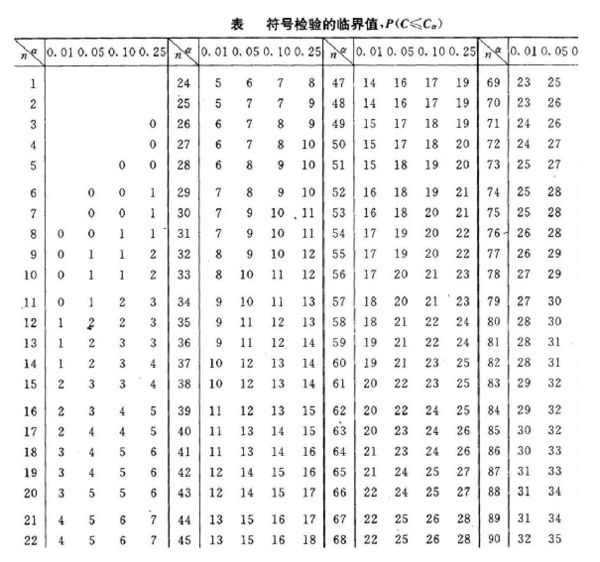
查符號檢驗表(表中N = n + + n − ):r = min(n + ,n − ),查表,如r>表值,差異不顯著,r≤表值,差異顯著。
符號檢驗的計算方法[1]
符號檢驗的具體檢驗方法因樣本大小的不同而不同。
1、小樣本(N<25)時的檢驗方法
例1:研究人員將三歲兒童經配對而成的實驗組進行顏色試驗教學,對照組不進行此種教學。後期測驗得分如表2。問顏色教學是否有顯著效果?
解:檢驗步驟:
(1)建立假設:
- H0:顏色教學無顯著效果
- H1:顏色教學有顯著效果
(2)求差數並記符號:計算X1 與X2每對數據的差數,“+”的個數n + = 7,“-”的個數n − = 3,差數為0不予考慮。於是有:n = n + + n − = 7 + 3 = 10。將n + 和n_中較小的一個記為r,本例r=3。
(3)統計決斷:根據n = n + + n − = 7 + 3 = 10及顯著性水平,查符號檢驗表尋找r的臨界值,r0.05 = 1,而實際的r=3, 有r > r0.05 。由於符號檢驗表是單側檢驗表,進行雙側檢驗時,其顯著性水平應乘以2。所以本例應在0.10顯著性水平上保留虛無假設,拒絕備擇假設。其結論為:顏色教學無顯著效果。
2、大樣本(N>25)時的檢驗方法
對於差值的正負號差異的檢驗本屬於二項分佈的問題,當樣本容量較大即(N>25)時,二項分佈近似於正態分佈,因此可用Z比率作為檢驗統計量。檢驗公式為:
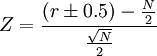 (1)
(1)
式中:r為n + 或n_的數值,N為n + 與n_之和。±0.5為校正數,當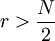 時用r-0.5,當
時用r-0.5,當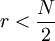 時用r+0.5。
時用r+0.5。
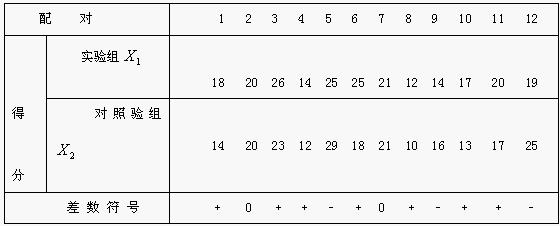
例2:某省幼教培訓中心,對30名幼兒園教師進行手工技能培訓,培訓前後的測驗結果如表2,試問培訓前後的兩次測驗結果差異是否顯著?
30名幼兒園教師培訓前後的兩次測驗結果
| 序 號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 培訓前X | 70 | 65 | 86 | 71 | 61 | 90 | 64 | 70 | 94 | 69 | 55 | 60 | 91 | 85 | 82 | 88 | 74 | 66 | 89 | 67 | 62 | 83 | 86 | 84 | 64 | 72 | 74 | 58 | 60 | 94 |
| 培訓後Y | 76 | 66 | 79 | 79 | 65 | 87 | 73 | 85 | 92 | 74 | 53 | 64 | 96 | 82 | 86 | 90 | 79 | 62 | 90 | 78 | 70 | 77 | 93 | 89 | 63 | 88 | 80 | 60 | 70 | 89 |
| 差數符號 | - | - | + | - | - | + | - | - | + | - | + | - | - | + | - | - | - | + | - | - | - | + | - | - | + | - | - | - | - | + |
解:檢驗步驟:
(1)建立假設:
- H0:手工技能培訓無顯著效果
- H1:手工技能培訓有顯著效果
(2)求差數並記符號:計算X1與X2每對數據的差數,“+”的個數n + = 9,“-”的個數n_=21,差數為0不予考慮。於是有: N = n + + n − = 9 + 21 = 30。將n + 和n − 中較小的一個記為r,本例r=9。
由於樣本容量比較大,則可使用(公式1)計算:
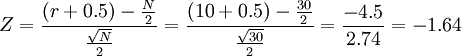
(3)統計決斷:因為|Z|<1.96,所以本例應在0.05顯著性水平上保留虛無假設,拒絕備擇假設。其結論為:手工技能培訓無顯著效果。
符號檢驗法的優點是不需要對所要檢驗的兩個總體的分佈形態做任何假定,並且計算簡便。其最大的缺點是它只考慮符號,不考察差數的大小,因而失去樣本所提供的一部分信息。對於同一樣本數據,採用符號檢驗的精確度,只相當於卡方檢驗的60%,因此除了小樣本,一般不使用符號檢驗。
附表:符號檢驗表
評論(共14條)
例2中在文字中說明r=9,在公式中使用的r=10,導致結果可能有問題……
謝謝指正,已進行更正。
請問符號檢驗表哪裡能找到?
補充了符號檢驗表
統計決斷這邊是不是有誤呀,Z的絕對值不是大於1.96嗎??
謝謝指正,原文已修正~
MBA智庫百科是可以自由參與的百科,如有發現錯誤和不足,您也可以參與修改編輯,只要通過網頁右上角的創建新帳號,創建用戶名後即可參與,期待您的加入哦!~
MBA智庫百科是可以自由參與的百科,如有發現錯誤和不足,您也可以參與修改編輯,點擊條目上方的編輯進入即可參與,期待您的加入!~
目的不一樣嘛,在只需要比較變化本身而不考慮變化量的情況下,簡單的符號檢測到是好用很多。
嗯,那張圖片的數字數字10還沒改過來呢
請問1.96是怎麼來的哈?
查表所得,F(n+m 0.05)








好!