卡方檢驗

出自 MBA智库百科(https://wiki.mbalib.com/)

卡方檢驗(Chi-square test/Chi-Square Goodness-of-Fit Test)

　　卡方檢驗是一種用途很廣的計數資料的假設檢驗方法。它屬於非參數檢驗的範疇，主要是比較兩個及兩個以上樣本率( 構成比）以及兩個分類變數的關聯性分析。其根本思想就是在於比較理論頻數和實際頻數的吻合程度或擬合優度問題。

　　它在分類資料統計推斷中的應用，包括：兩個率或兩個構成比比較的卡方檢驗；多個率或多個構成比比較的卡方檢驗以及分類資料的相關分析等。

　　卡方檢驗是以χ²分佈為基礎的一種常用假設檢驗方法，它的無效假設H₀是：觀察頻數與期望頻數沒有差別。

　　該檢驗的基本思想是：首先假設H₀成立，基於此前提計算出χ²值，它表示觀察值與理論值之間的偏離程度。根據χ²分佈及自由度可以確定在H₀假設成立的情況下獲得當前統計量及更極端情況的概率P。如果P值很小，說明觀察值與理論值偏離程度太大，應當拒絕無效假設，表示比較資料之間有顯著差異；否則就不能拒絕無效假設，尚不能認為樣本所代表的實際情況和理論假設有差別。

　　χ²值表示觀察值與理論值之間的偏離程度。計算這種偏離程度的基本思路如下。

　　(1)設A代表某個類別的觀察頻數，E代表基於H₀計算出的期望頻數，A與E之差稱為殘差。

　　(2)顯然，殘差可以表示某一個類別觀察值和理論值的偏離程度，但如果將殘差簡單相加以表示各類別觀察頻數與期望頻數的差別，則有一定的不足之處。因為殘差有正有負，相加後會彼此抵消，總和仍然為0，為此可以將殘差平方後求和。

　　(3)另一方面，殘差大小是一個相對的概念，相對於期望頻數為10時，期望頻數為20的殘差非常大，但相對於期望頻數為1 000時20的殘差就很小了。考慮到這一點，人們又將殘差平方除以期望頻數再求和，以估計觀察頻數與期望頻數的差別。

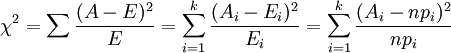　　(i=1，2，3，…，k)

　　其中，A_i為i水平的觀察頻數，E_i為i水平的期望頻數，n為總頻數，p_i為i水平的期望頻率。i水平的期望頻數E_i等於總頻數n×i水平的期望概率p_i，k為單元格數。當n比較大時，χ²統計量近似服從k-1(計算E_i時用到的參數個數)個自由度的卡方分佈。

　　作為學術界的領袖，Pearson先生當初發表在《哲學雜誌》上的χ²論文題目為：On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling.

　　由卡方的計算公式可知，當觀察頻數與期望頻數完全一致時，χ²值為0；觀察頻數與期望頻數越接近，兩者之間的差異越小，χ²值越小；反之，觀察頻數與期望頻數差別越大，兩者之間的差異越大，χ²值越大。換言之，大的χ²值表明觀察頻數遠離期望頻數，即表明遠離假設。小的χ²值表明觀察頻數接近期望頻數，接近假設。因此，χ²是觀察頻數與期望頻數之間距離的一種度量指標，也是假設成立與否的度量指標。如果χ²值“小”，研究者就傾向於不拒絕H₀；如果χ²值大，就傾向於拒絕H₀。至於χ²在每個具體研究中究竟要大到什麼程度才能拒絕H₀，則要藉助於卡方分佈求出所對應的P值來確定。

　　卡方分佈本身是連續型分佈，但是在分類資料的統計分析中，顯然頻數只能以整數形式出現，因此計算出的統計量是非連續的。只有當樣本量比較充足時，才可以忽略兩者間的差異，否則將可能導致較大的偏差具體而言，一般認為對於卡方檢驗中的每一個單元格，要求其最小期望頻數均大於1，且至少有4／5的單元格期望頻數大於5，此時使用卡方分佈計算出的概率值才是準確的。如果數據不符合要求，可以採用確切概率法進行概率的計算。

　　1、四格表資料的卡方檢驗

　　四格表資料的卡方檢驗用於進行兩個率或兩個構成比的比較。

　　1）專用公式：

　　若四格表資料四個格子的頻數分別為a，b，c，d，則四格表資料卡方檢驗的卡方值=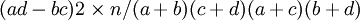，自由度v=(行數-1)(列數-1)

　　2)應用條件：

　　要求樣本含量應大於40且每個格子中的理論頻數不應小於5。當樣本含量大於40但理論頻數有小於5的情況時卡方值需要校正，當樣本含量小於40時只能用確切概率法計算概率。

　　2、行×列表資料的卡方檢驗

　　行×列表資料的卡方檢驗用於多個率或多個構成比的比較。

　　1）專用公式：

　　r行c列表資料卡方檢驗的卡方值=

　　2)應用條件：

　　要求每個格子中的理論頻數T均大於5或1<T<5的格子數不超過總格子數的1/5。當有T<1或1<T<5的格子較多時，可採用並行併列、刪行刪列、增大樣本含量的辦法使其符合行×列表資料卡方檢驗的應用條件。而多個率的兩兩比較可採用行×列表分割的辦法。

　　3、列聯表資料的卡方檢驗

　　同一組對象，觀察每一個個體對兩種分類方法的表現，結果構成雙向交叉排列的統計表就是列聯表。

　　1）R×C 列聯表的卡方檢驗：

　　R×C 列聯表的卡方檢驗用於R×C列聯表的相關分析，卡方值的計算和檢驗過程與行×列表資料的卡方檢驗相同。

　　2）2×2列聯表的卡方檢驗：

　　2×2列聯表的卡方檢驗又稱配對記數資料或配對四格表資料的卡方檢驗，根據卡方值計算公式的不同，可以達到不同的目的。當用一般四格表的卡方檢驗計算時，卡方值=(ad-bc)2n/(a+b)(c+d)(a+c)(b+d)，此時用於進行配對四格表的相關分析，如考察兩種檢驗方法的結果有無關係；當卡方值=( | b − c | − 1)²/(b+c)時，此時卡方檢驗用來進行四格表的差異檢驗，如考察兩種檢驗方法的檢出率有無差別。

　　列聯表卡方檢驗應用中的註意事項同R×C表的卡方檢驗相同。

　　卡方檢驗最常見的用途就是考察某無序分類變數各水平在兩組或多組間的分佈是否一致實際上，除了這個用途之外．卡方檢驗還有更廣泛的應用。具體而言，其用途主要包括以下幾個方面：

　　(1)檢驗某個連續變數的分佈是否與某種理論分佈相一致。如是否符合正態分佈、是否服從均勻分佈、是否服從Poisson分佈等。

　　(2)檢驗某個分類變數各類的出現概率是否等於指定概率。如在36選7的彩票抽獎中，每個數字出現的概率是否各為1／36；擲硬幣時，正反兩面出現的概率是否均為0．5。

　　(3)檢驗某兩個分類變數是否相互獨立。如吸煙(二分類變數：是、否)是否與呼吸道疾病(二分類變數：是、否)有關；產品原料種類(多分類變數)是否與產品合格(二分類變數)有關。

　　(4)檢驗控制某種或某幾種分類因素的作用以後，另兩個分類變數是否相互獨立。如在上例中，控制性別、年齡因素影響以後，吸煙是否和呼吸道疾病有關；控制產品加工工藝的影響後，產品原料類別是否與產品合格有關。

　　(5)檢驗某兩種方法的結果是否一致。如採用兩種診斷方法對同一批人進行診斷，其診斷結果是否一致；採用兩種方法對客戶進行價值類別預測，預測結果是否一致。

　　適用於四格表應用條件：

　　1)隨機樣本數據。兩個獨立樣本比較可以分以下3種情況：

　　(1)所有的理論數T≥5並且總樣本量n≥40，用Pearson卡方進行檢驗。

　　(2)如果理論數T＜5但T≥1，並且n≥40，用連續性校正的卡方進行檢驗。

　　(3)如果有理論數T＜1或n＜40，則用Fisher’s檢驗。

　　2)卡方檢驗的理論頻數不能太小。

　　R×C表卡方檢驗應用條件：

　　(1)R×C表中理論數小於5的格子不能超過1／5；

　　(2)不能有小於1的理論數。如果實驗中有不符合R×C表的卡方檢驗，可以通過增加樣本數、列合併來實現。

　　1.應用實例——適合度檢驗

　　實際執行多項式試驗而得到的觀察次數，與虛無假設的期望次數相比較，稱為卡方適度檢驗，即在於檢驗二者接近的程度，利用樣本數據以檢驗總體分佈是否為某一特定分佈的統計方法。這裡以擲骰子為例介紹適度檢驗的方法。

　　【例1】

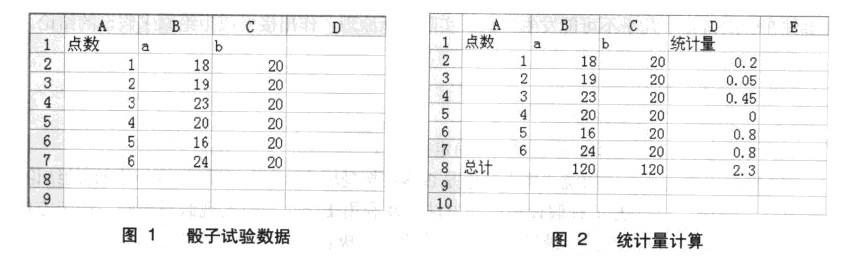
　　(1)假設擲一骰子120次，各點數共出現次數為a，b為各點數出現的期望值120×1/6=20，建立工作表文件，如圖1所示。

　　(2)設置零假設H₀：觀察分佈等於期望分佈。

　　(3)計算卡方檢驗統計量，如圖2所示。

　　D2=(B2-C2)^2/C2

　　D8=SUM(D2:D7)

　　(4)確定自由度，(6-1)×(2-1)=5；選擇顯著水平α=0.05。

　　(5)利用Excel提供的CHIINV函數求臨界值，在D9單元格中鍵入“=CHIINV(0.05，5)”按回車鍵，得臨界值11.07。

　　(6)比較臨界值和統計量，11.07>2.3，即臨界值大於統計量，故差異不顯著，接受H₀。

　　2.應用實例2——獨立性檢驗

　　卡方獨立性檢驗是用來檢驗兩個屬性間是否獨立。一個變數作為行，另一個變數作為列。下麵一例便是介紹卡方獨立性檢驗的方法。

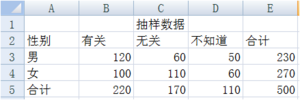
　　【例2】某機構欲瞭解現在性別與收入是否有關，他們隨機抽樣500人，詢問對此的看法，結果分為“有關、無關、不好說，，三種答案，圖3中縣調查得到的數據。

圖3

　　下麵是利用Excel解決此問題的步驟。

　　(1)零假設H₀：性別與收入無關。

　　(2)確定自由度為(3-1)×(2-1)=2，選擇顯著水平α=0.05。

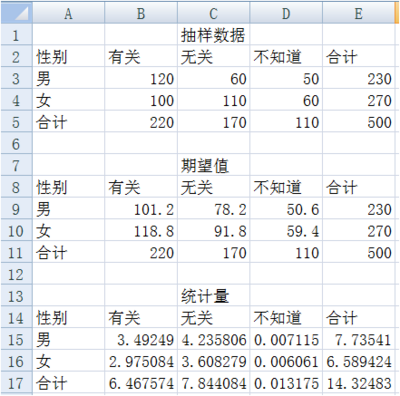
　　(3)求解男女對收入與性別相關不同看法的期望次數，這裡採用所在行列的合計值的乘積除以總計值來計算每一個期望值，如圖4所示，在單元格B9中鍵入“=B5*E3/E5”，同理(第一個等於號理解為在單元格中鍵入)：

• B10=“=B5*E4/E5，
• C9=“=C5*E3/E5”，
• C10=“=C5*E4/E5”，
• D9=“=D5*E3/E5”，
• D10=“=D5*E4/E5”。

圖4

　　(4)利用卡方統計量計算公式計算統計量，在單元格B15中鍵入“=(B3-B9)^2/B9”，其餘單元格依次類推，結果如圖5所示。

圖5

　　(5)利用Excel提供的CHIINV函數計算顯著水平為0.05，自由度為2卡方分佈的臨界值，在Excel單元格中鍵入“=CHIINV(0.05,2)”按回車鍵，得臨界值為5.9915。

　　(6)比較統計量度和臨界值，統計量14.32483大於臨界值5.9915，故拒絕零假設。

　　3．應用實例3——統一性檢驗

　　檢驗兩個或兩個以上總體的某一特性分佈，也就是各“類別”的比例是否統一或相近，一般稱為卡方統一性檢驗或者卡方同質性檢驗。下麵一例便是利用卡方統一性檢驗的例子。

　　【倒3】某咨詢公司想瞭解南京和北京的市民對最低生活保障的滿意程度是否相同。他們從南京抽出600居民，北京抽取600居民，每個居民對滿意程度(非常滿意、滿意、不滿意、非常不滿意)任選一種，且只能選一種。將統計結果鍵入Excel工作表中，如圖6所示。

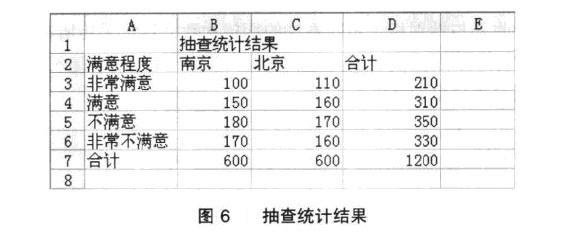
　　下麵是利用Excel解決此問題的步驟。

　　(1)零假設H₀：南京和北京居民對最低生活保障滿意程度的比例相同。

　　(2)確定自由度為(4-1)×(2-1)=3，選擇顯著水平α=0.05。

　　(3)求解卡方檢驗的l臨界值，在Excel單元格中鍵入“=CHIINV(0.05，3)”，按回車鍵得臨界值為7.81。

　　(4)計算北京和南京不同滿意程度的期望值，在單元格B11和C11中分別鍵入“=$B$7*D3/$D$7”和“=$C$7*D3/$D$7”，選中B11：C11，按住C11右下角填充控制點，填充至C14。

　　(5)計算卡方統計量，在單元格B19中鍵入“=(B3-B11)^2/B11”，其餘單元格依次類推，結果如圖7所示。

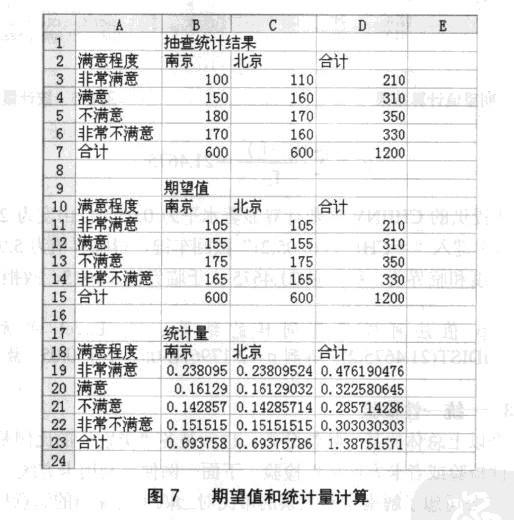
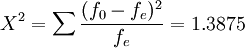
　　(6)比較統計量和臨界值，統計量1.3875小於臨界值7.81，故接受零假設。