主觀期望效用理論
出自 MBA智库百科(https://wiki.mbalib.com/)
主觀期望效用理論(Subjective Expected Utilities,SEU模式)
目錄 |
主觀期望效用理論模式是建立在Von Neumann和Morgenstern所設計的公理體系基礎上的。包含效用關係的完備性(Completeness)、傳遞性(transitivity)與替換性(Substitution)、決策者偏好的一致性(preference)等,但後來的研究發現該理論的優勢原則和無差異原則與現實決策不符。
主觀期望效用理論仍堅持,每個結果都是期望概率與其價值概率的乘積。但是,這個價值成分是主觀的,依賴於個體差異。
這個模型假定,人們作出決策時是根據主觀期望效用值的高低來進行的。我們可以通過瞭解概率和一系列決策選項的效用,就可以根據這個模型預測出一個“合理”的或內在一致的選擇。
觀期望效用模型由於其簡單靈活,已經成為分析人們在不確定情況下決策行為的重要理論。但是由於現實世界的複雜性,人們不可能設定單個先驗分佈來描述不確定事件,因此主觀期望效用模型在實際決策中是有缺陷的。針對這一現象,人們對主觀期望效用理論的公理體系進行了一些改造,主要有Schmeidler提出的Choquet期望效用模型及Gilboa和Schmeidler提出的多先驗期望效用模型。
定理:若決策者按主觀概率模型對事件結果發生的可能性作出主觀反應,則所有結果的主觀概率之和等於1,即:

由主觀概率模型和安全繫數的性質可知,定理的結論是顯然的。
推論:若一不確定性選擇僅有兩個可能結果 a1 > a2 ,它們的客觀概率分別為p1、1 − p1,則對於決策者所偏好的結果a1 來說,其主觀概率為該結果的客觀概率所對應的安全繫數SC(p1),另一個結果a2 的主觀概率則為1-SC(p1)。這個推論是主觀概率模型的一個特例。
定理:說明用主觀概率模型解決了直接用安全繫數代替客觀概率和一些等級依賴理論中出現的總概率和不為1 的問題;用主觀概率πi 代入期望效用模型中代替客觀概率pi,就得到了主觀期望效用模型(Subjective Expected Utility Model):

案例一:主觀期望效用模型在保險產品定價中的應用[1]
保險學說到底是一門關於如何用財務手段處理風險的科學,保險定價實質上是對風險的定價。傳統的期望效用理論認為保險定價的可行性緣於保險人與投保人在效用函數上的差別,保險人的效用函數相對於投保人的更不“懼怕”風險,對風險的定價比投保人的低,使得G<H,從而保險價格P 可以在介於由G與H之間實現。
但是由於效用函數具有很強的主觀性,沒有足夠的客觀證據或理論證明保險人的效用函數的Arrow-Pratt 指數會比投保人的低,從而使傳統的效用理論下的定價模式受到了廣泛的質疑。下麵,我們運用主觀期望效用理論的觀點,從保險人和投保人所處於的不同的風險環境出發,研究保險人與投保人在確定性效應函數值上的差異,進而對保險定價及定價的可行性進行分析。由於效用函數的主觀性,我們很難客觀的判斷保險人與投保人的效用函數的異同,在不失一般性的前提下可以假設兩者的效用函數是沒有差別的,將分析的重心放在確定性效應函數值v(p)上;同時,接受Daniel Kahneman和Amos Tversky的觀點,即認為決策者的效用值只與其財富的變化值有關,而與財富的初始值無關。
首先從投保人的角度來考察其確定性效應函數值v1(p)。假設財產持有人面臨著以期望值為q 的概率失去某一額度的財產W 的風險,現在要考慮的問題就是他會願意以什麼樣的價格為這份財產投保?
由於投保人失去W 的平均可能性是q,那麼,他仍擁有這一部分財產的可能性p=1-q,我們也可以從另一個角度認為他以p 的概率“獲取”W,以q 的概率什麼也得不到。那麼,由主觀期望效用理論,記該財產持有人的確定性效應函數值為v1(p)。保險公司也是害怕風險的,一般通過核保拒絕承保風險很大的標的,即q 的值比較小,在這種情況下p>ε,從而一般有v1(p)<p,也就是說財產持有人主觀上認為自己不失去W 的可能性達不到p,這裡除了因為確定性效應函數是凸函數以外,還可以從下麵兩個方面進行說明:
1、風險厭惡。大量的實證研究已經證明瞭在一般情況下,人們會產生一種悲觀主義的心態,所以財產持有人往往由於有害怕失去財產的心理,所以會導致其主觀上將q 的值放大,使他們認為自己仍將持有W 的可能性的自信心不足。
2、q 的不確定性。在現實中,人們一般對損失的概率q 都只有一個期望的概念,但具體到自身面對的風險,其概率的取值是不確定的。從上面提到的Ellsberg 悖論中可以看出,人們對不確定的風險的厭惡程度要強於對確定性的風險的厭惡程度。所以,q 的不確定性會導致人們對這種風險的厭惡程度加深。
綜上所述,在面臨失去財產的風險時,財產持有人對仍然擁有該財產的確定性效應函數值v1(p)會明顯地下凸,即:v1(p)<p。
現在,再從保險人所處的風險環境分析保險人的確定性效應函數值。若是考慮每一單位保單,在無免賠全額投保的情況下,保險人一旦承保,則投保人所面臨的風險便轉移到保險人身上了,在這種意義下,保險人(承保時)所面對的風險與投保人(不投保時)所面對的風險是沒有區別的,這時,兩者的確定性效應函數也應該沒有差別。但是,如果我們從整體上進行考慮,情況就不一樣了,財產持有人所面臨的風險是單一的、不穩定的風險;而保險人一般會承保大量同質或類似的標的,這樣,按照概率論中的大數定律,保險人所面對的風險環境是一個相對比較穩定的、有規律的風險環境,而且其承保的標的越多,損失(索賠)發生的概率(或比例)就越穩定,保險人所面對的風險環境也就越穩定。這樣,保險人對損失發生概率的主觀看法就會較投保人(財產持有人)更接近於客觀概率,從而其確定性效應函數值v2(p)也將更接近於p,從而一般有:
v1(p) < v2(p)< p (1)
實際上,現實中保險公司對每一類型的保單都有數以萬計保戶,所以,在理論上保單發生索賠的概率是非常穩定的,可以認為v2(p)=p。
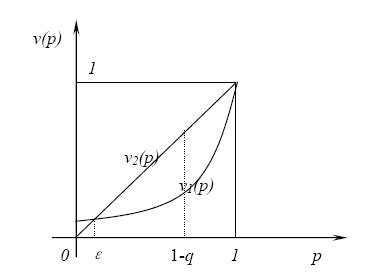
因此,保險人和投保人所處的風險環境是不一樣的,從而他們對風險的主觀看法也將不一致,所以,他們各自的確定性效應函數v(p)的曲線是不一樣的,有如下圖1 所示:(假設v2(p)=p)
圖1 保險人、投保人的確定性效應函數(The Certainty Effect Function of Insurers & Insured’s)
對於財產W 所面臨的風險,與傳統的期望效用理論的原理類似,財產持有人願意投保的最高保費(臨界保費)應該為其在投保時的主觀期望效用與不投保時的主觀期望效用相等時的保費值H,滿足:
![v_1(p)\cdot u(W)+[1-v_1(p)]\cdot u(o)=v_1(p)\cdot u(W)=u(W-H)](/w/images/math/b/6/8/b685a8c9313a8ff9d5659bb4eb9192b5.png) (2)
(2)
而對於保險人來說,他所願意承保的最低保費(臨界保費)G也是在承保時的主觀期望效用值![v_2(p)\cdot u(G)+[1-v_2(p)]\cdot u(G -W)](/w/images/math/f/6/b/f6b55d7c65c83921c002f713dbf1cde6.png) 與不承保時主觀期望效用值u(0)相等時的保費值。滿足:
與不承保時主觀期望效用值u(0)相等時的保費值。滿足:
![v_2(p)\cdot u(G)+[1-v_2(p)]\cdot u(G -W)](/w/images/math/f/6/b/f6b55d7c65c83921c002f713dbf1cde6.png)
![=v_2(p)\cdot u(G)-[1-v_2(p)]\cdot u(W-G)=u(o)=0](/w/images/math/4/1/7/41718b29b2c1ae2a7b13b8719a3f0046.png) (3)
(3)
由(3)式得:
![v_2(p)\cdot u(G)-[1-v_2(p)]\cdot u(W-G)=u(o)=0](/w/images/math/e/d/5/ed5183cec0337311015e3335d38e297d.png)
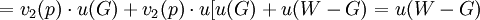 (4)
(4)
∵ v2(p)> v1(p) 且 u(G)+u(W-G)>u(W)
∴ u(W − G) > u(W − H)
∴G < H (5)
這樣,保費價格P 在一般情況下(只要投保人的確定性效應函數值是下凸的)總可以在介於G與H之間實現,這是由於保險人和投保人所處的不同的風險環境的結果,與各自的效用函數無關,其具體的取值取決於競爭狀況及保險公司的內部管理效率。
從上面的整個推理過程可以看出,保險人和投保人之間保險合同能夠簽訂的原因關鍵在於式1的成立,即v1(p)<v2(p)<p。這個不等式包含兩個條件:首先,保險人必須能夠聚集大量的同質或類似的保單,因為只有這樣才能使自身所面臨的風險環境趨於穩定,才能確保保險人所依賴的大數法則的實現,才能在風險環境上保持對投保人的優勢;其次,保險人設計的保單所涉及的風險必須具有針對性,必須充分分析投保人的心理特征,針對投保人所厭惡的風險來設計保單,這樣才能保證式1 的成立。
最後,需要特別指出的是,雖然保險人處在一個相對穩定的風險環境之中,但並不意味著保險公司的經營是沒有風險的。保險公司除了要面對投機風險、管理風險、財務風險以外,還有兩個基於承保標的的潛在的風險:一是風險的積聚,現實社會中常常會因為天災人禍如地震等導致大量的標的在同一時間內發生損失從而導致在短時間內“積聚”了大量的索賠,從而可能影響到保險人的財務穩定甚至導致危機;二是巨災風險,有時候雖然只有一件或少數幾件索賠發生,但由於承保標的發生的損失過於龐大,如航空事件、9.11 事件等,這種巨大的損失額往往使保險人促不及防,是保險公司極為忌諱的風險。在這兩種情況下,保險人所依賴的大數法則已經失去了作用,保險人面對的這兩類風險也是不穩定的,這時候保險人就變得和投保人一樣“懼怕”風險了,他們一般都是選擇安排再保險來對自己所面對的這些風險進行“保險”,使得在發生巨額索賠時仍能夠維持財務上的穩定。這也說明傳統的期望效用理論認為保險人與投保人之間對財富或其他物質的主觀看法存在差異是缺乏客觀依據的,在面對風險損失時,兩者其實是同樣存在風險迴避意識的。
綜上所述,可以得出結論:保險定價的可行性並不在於保險人與投保人對財富的主觀看法——效用函數上存在差別,而是在於保險人與投保人所處的不同的風險環境,保險人通過承保大量的同質標的使其所面臨的損失概率趨於穩定,提高了自己的確定性效應,從而有“能力”承保投保人的風險,當保險人自身也面臨不穩定的風險時,也是“懼怕”風險的,將通過再保險的方式對自己所面臨的風險進行“保險”。同時,我們可以從中得到一個啟示就是:心理因素在保險精算中占據著重要的地位,保險人設計的保單所涉及的風險必須具有針對性,必須在充分分析投保人的心理特征的基礎上,針對投保人所厭惡的風險來設計保單,這樣才能吸引足夠的消費者來購買保單,確保大數法則的實現。
- ↑ 鄭振龍,何凱浩.主觀期望效用模型在保險產品定價中的應用[J].金融評論,2007,(2)