鮑摩爾模型
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
威廉·鮑摩爾(William Baumol)第一次將機會成本與交易成本結合在一起,提出了現金管理的正式模型。鮑摩爾模型(The Baumol Model)可以用來確定目標現金餘額。
鮑摩爾模型的基本原理是將現金持有量和有價證券聯繫起來權衡,即將現金的持有成本同轉換有價證券的成本進行權衡,以求得兩者相加總成本最低時的現金餘額從而得出目標現金金額。
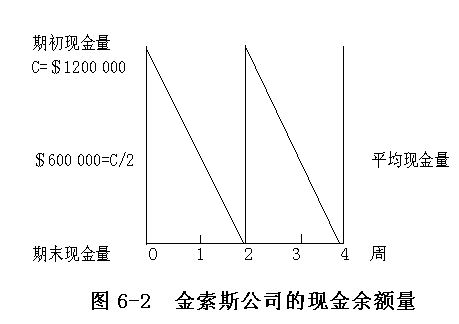
假設金索斯公司(Golden Socks Corporation)在第0周的現金餘額C=120萬美元,且每周的現金流出量比現金流入量多60萬美元。該公司的現金餘額在第二周末將降為零,即在這兩周內其平均現金餘額為60萬美元。在第二周末,金索斯公司就必須出售有價證券或是通過借貸來補充現金了。圖6-2說明瞭這一情況。
如果把C設得更高一些,比如,設為240萬美元,這樣在企業需要出售有價證券之前,現金就可以維持四周,但是企業的平均現金餘額也隨之(從60萬美元)提高到120萬美元。如果把C設為60萬美元,那麼現金在一周內就將耗盡,而企業也必須更頻繁得補充現金,雖然這樣,企業的平均現金餘額卻從60萬美元降至30萬美元。
由於補充現金時必然發生交易成本(例如,出售有價證券時需支付的經紀費用),因此建立大量的初始現金餘額將降低與現金管理有關的交易成本。然而,平均現金餘額越大,機會成本(本可以有售出的有價證券得到的收益)也就越大。
為瞭解決這一問題,金索斯公司必須明確以下三點:
F=售出證券以補充現金的固定成本
T=在相關的計劃周期(例如,一年)內交易的現金總需要量
K=持有現金的機會成本(即有價證券的利率)
在此基礎上,金索斯公司就可以確定任一特定現金餘額政策的總成本,並隨之確定最佳的現金餘額政策了。
以美元計算的總機會成本等於現金餘額乘以利率,或表示為:
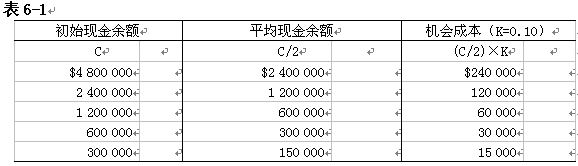
機會成本=(C/2)×K
表6-1列示幾種不同選擇的機會成本:
金索斯公司的交易成本可以通過計算該年起出售有價證券的次數而確定.該年的現金支出總額為60萬美元×52周=3 120萬美元。如果將初始現金餘額設為120萬美元,那麼金索斯公司每兩周就必須出售120萬美元有價證券。這樣,我們可以得到交易成本為:
其計算公式為:
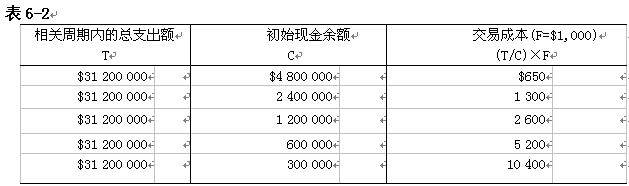
交易成本($)=(T/C)×F
可選擇方案的交易成本如表6-2所示:
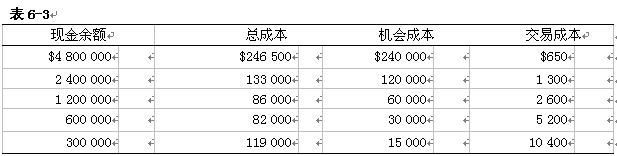
現金餘額的總成本是由機會成本加上交易成本構成:如表6-3所示。
總成本=機會成本+交易成本
=(C/2)×K+(T/C)×F
我們可以從上表中看到,現金餘額為60萬美元時對應的是所列出的可能總成本的最低值為82 000美元。但是,現金餘額為700萬美元,或500萬美元,或是其他可能值時總成本又是多少呢?為了精確的確定最低總成本,金索斯公司就必須令隨著現金餘額上升而產生的交易成本的邊際減少額等於隨著餘額上升的機會成本的邊際增加額。目標現金餘額即為互為消漲的二者的相遇點。
總成本(TC)=(C/2)×K+(T/C)×F
如果我們將總成本對應於現金餘額求導並令其等於零,就可以得到:
如果F=1 000萬美元,T=3 120萬美元,且K=10%,那麼C=789 936.71美元。
鮑摩爾模型是對現金管理的一大貢獻,但這一模型也具有以下局限性:
①該模型假設企業的支出率不變。但實際中,由於到期日的不同及無法對成本進行準確預測,而只能對開支進行部分管理。
②該模型假設計劃期內未發生現金收入。事實上,絕大多數企業在每一個工作日內都將既發生現金流入也發生現金流出。
③未考慮安全現金庫存。為了降低現金短缺或耗盡的可能性,企業極有可能擁有一個安全現金庫存。但是,如果企業可以實現在幾小時內售出有價證券或進行借貸,安全現金庫存量就可以達到最小。
鮑摩爾模型可能是最簡單、最直觀的確定最佳現金量的模型,但其最大的不足是假定現金量是離散的、確定的。

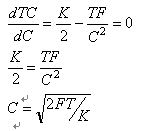








好