鲍摩尔模型
出自 MBA智库百科(https://wiki.mbalib.com/)
目录 |
威廉·鲍摩尔(William Baumol)第一次将机会成本与交易成本结合在一起,提出了现金管理的正式模型。鲍摩尔模型(The Baumol Model)可以用来确定目标现金余额。
鲍摩尔模型的基本原理是将现金持有量和有价证券联系起来权衡,即将现金的持有成本同转换有价证券的成本进行权衡,以求得两者相加总成本最低时的现金余额从而得出目标现金金额。
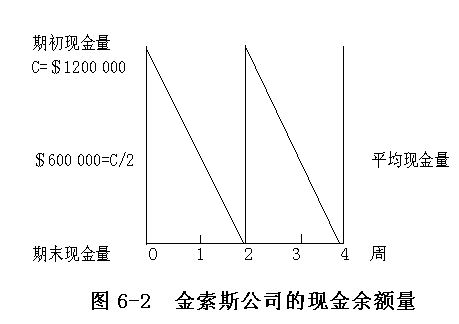
假设金索斯公司(Golden Socks Corporation)在第0周的现金余额C=120万美元,且每周的现金流出量比现金流入量多60万美元。该公司的现金余额在第二周末将降为零,即在这两周内其平均现金余额为60万美元。在第二周末,金索斯公司就必须出售有价证券或是通过借贷来补充现金了。图6-2说明了这一情况。
如果把C设得更高一些,比如,设为240万美元,这样在企业需要出售有价证券之前,现金就可以维持四周,但是企业的平均现金余额也随之(从60万美元)提高到120万美元。如果把C设为60万美元,那么现金在一周内就将耗尽,而企业也必须更频繁得补充现金,虽然这样,企业的平均现金余额却从60万美元降至30万美元。
由于补充现金时必然发生交易成本(例如,出售有价证券时需支付的经纪费用),因此建立大量的初始现金余额将降低与现金管理有关的交易成本。然而,平均现金余额越大,机会成本(本可以有售出的有价证券得到的收益)也就越大。
为了解决这一问题,金索斯公司必须明确以下三点:
F=售出证券以补充现金的固定成本
T=在相关的计划周期(例如,一年)内交易的现金总需要量
K=持有现金的机会成本(即有价证券的利率)
在此基础上,金索斯公司就可以确定任一特定现金余额政策的总成本,并随之确定最佳的现金余额政策了。
以美元计算的总机会成本等于现金余额乘以利率,或表示为:
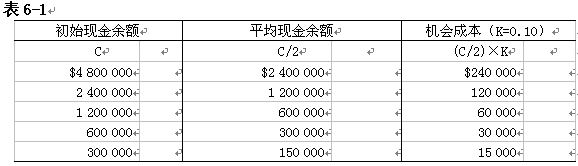
机会成本=(C/2)×K
表6-1列示几种不同选择的机会成本:
金索斯公司的交易成本可以通过计算该年起出售有价证券的次数而确定.该年的现金支出总额为60万美元×52周=3 120万美元。如果将初始现金余额设为120万美元,那么金索斯公司每两周就必须出售120万美元有价证券。这样,我们可以得到交易成本为:
其计算公式为:
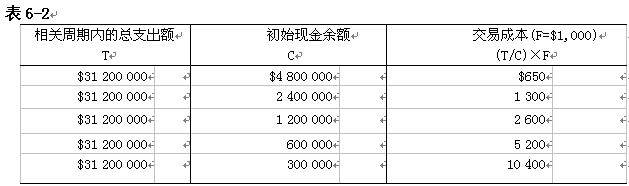
交易成本($)=(T/C)×F
可选择方案的交易成本如表6-2所示:
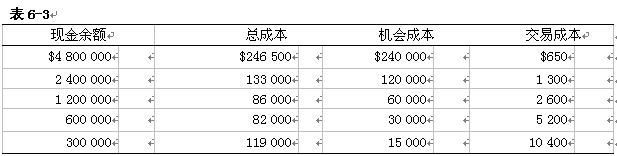
现金余额的总成本是由机会成本加上交易成本构成:如表6-3所示。
总成本=机会成本+交易成本
=(C/2)×K+(T/C)×F
我们可以从上表中看到,现金余额为60万美元时对应的是所列出的可能总成本的最低值为82 000美元。但是,现金余额为700万美元,或500万美元,或是其他可能值时总成本又是多少呢?为了精确的确定最低总成本,金索斯公司就必须令随着现金余额上升而产生的交易成本的边际减少额等于随着余额上升的机会成本的边际增加额。目标现金余额即为互为消涨的二者的相遇点。
总成本(TC)=(C/2)×K+(T/C)×F
如果我们将总成本对应于现金余额求导并令其等于零,就可以得到:
如果F=1 000万美元,T=3 120万美元,且K=10%,那么C=789 936.71美元。
鲍摩尔模型是对现金管理的一大贡献,但这一模型也具有以下局限性:
①该模型假设企业的支出率不变。但实际中,由于到期日的不同及无法对成本进行准确预测,而只能对开支进行部分管理。
②该模型假设计划期内未发生现金收入。事实上,绝大多数企业在每一个工作日内都将既发生现金流入也发生现金流出。
③未考虑安全现金库存。为了降低现金短缺或耗尽的可能性,企业极有可能拥有一个安全现金库存。但是,如果企业可以实现在几小时内售出有价证券或进行借贷,安全现金库存量就可以达到最小。
鲍摩尔模型可能是最简单、最直观的确定最佳现金量的模型,但其最大的不足是假定现金量是离散的、确定的。

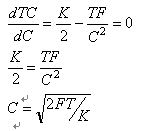








好