項目時間計劃
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
什麼是項目時間計劃[1]
項目時間計劃是對項目所有活動的順序和工期進行安排、協調，並確定項目的總工期。最終的進度計劃通常要放在日曆表上。
項目時間計劃的依據[2]
項目時間計劃的詳細依據是對所有可識別的假設和限制的文件化。這種附加細節到底應該有多少取決於項目的特點和要求，例如在建設項目中，最可能包含資源柱狀圖、現金流計劃以及預製和交付的時間計劃等事項；而在電子項目中，很可能只包含資源柱狀圖。通常情況下，作為詳細依據適用的信息包括：
1．隨時間進度而改變的資源需求，通常以資源柱狀圖的形式來顯示。
2．可替代的時間計劃，如最好的或最壞的情況，帶有或不帶有強制要求的資源等。
3．進度儲備或進度風險評估。
項目時間計劃的制定[3]
制定項目時間計劃是為了控制時間和節約時間，而項目一般都具有嚴格的時間要求，因此使得時間計劃在項目管理中變得很重要。項目時間計劃是在工作分解結構的基礎上對活動、項目做出的一系列的時間計劃，它主要說明哪些工作必須於何時完成，以及完成每一項任務所需要的時間，有時也表示出每項活動所需的人數。
一、項目進度計劃的時間參數
項目進度計劃記錄了項目中每一活動的計劃和實際的開始日期、完成日期和周期。在大多數複雜的進度計劃中，都會用到下列時間參數以及相關的時間參數：
(一)工期
工期是完成活動所需的時間。在每個活動開始之前，都有一個估算的周期，而在每個活動開始之後完成之前，我們也可以估算剩餘周期。一旦活動已經完成，我們就可以記錄實際周期。
(二)最早開始時間(ES)和最早結束時間(EF)
最早開始時間是指某項活動能夠開始的最早時間。它可以在項目的預計開始時間和所有正常的工期估計基礎上計算出來。最早結束時間是指某一活動能夠完成的最早時間，它可以在這項活動最早開始時間的基礎上加上這項活動的工期估計計算出來。
EF=ES+工期估計
(三)最遲開始時間(LS)和最遲結束時間(LF)
最遲開始時間是指為了使項目在要求完工的時間內完成，某項活動必須開始的最遲時間。最遲結束時間是指為了使項目在完工時間內完成，某項活動必須完成的最遲時間。它可以在項目的要求完工時間和各項緊隨活動工期估計的基礎上計算出來。最遲開始時間可以用這項活動的最遲結束時間減去它的工期估算計算出來。
LS=LF-工期估計
(四)時差
如果最遲開始時間與最早開始時間不同，那麼該活動的開始時間就可以浮動，稱之為時差：
時差=最遲開始時間-最早開始時間
同理，如果最遲結束時間和最早結束時間不同，那麼該活動的結束時間也可以浮動，同樣稱為該活動的時差：
時差=最遲結束時間-最早結束時間
二、編製項目時間計劃的方法與工具
(一)關鍵路線法(CPM)
關鍵路線法(CPM)是一種常用的數學分析技術，是根據網路圖和各活動所需時間(估計值)，計算每一活動的最早或最遲開始和結束時間。但計算時並沒有考慮資源限制，這樣算出的日期並不是實際進度，而是表示所需的時間長短，考慮活動的資源限制和其他約束條件，把活動安排在上述時間區間內。在計算出作業時間、節點時間和活動時間後，結合考慮時差，可以求出項目的關鍵路線。關鍵路線法(CPM)的關鍵是計算總時差，這樣可決定哪一活動有最小時間彈性。CPM演算法也在其他類型的數學分析中得到應用。CPM演算法的具體步驟如下：
1．求出各活動的ES和EF。我們可以通過公式求出各活動的時間參數ES和EF，這是通過正向計算得到的。即從項目開始沿網路圖到項目完成進行計算。在進行這些正向計算時必須註意：某項活動的最早開始時間必須相同或晚於直接指向這一活動的所有活動的最早結束時間中的最晚時間。
2．求出各活動的LF和LS。計算各活動的LF和LS，可以通過反向推算得出。即從項目完成沿網路圖到項目的開始進行推算。在進行這類推算時也必須註意：某項活動的最遲結束時間必須相同或者早於該活動直接指向的所有活動最遲開始時間的最早時間。
3．計算時差。要分別計算出活動總時差和每項工作活動的單時差。活動總時差是指在不影響整個項目完工時間的條件下，某項活動最遲開始時間與最早開始時間的差。它表明該活動開始時間允許推遲的最大限度。活動單時差是指在不影響下一活動的最早開始時間的前提下，該活動完工期可能有的機動時間。
4．找出關鍵路線。在一個網路圖中，總時差為零的活動，稱為關鍵活動。時差為零的節點稱為關鍵節點。一個從始點到終點，沿箭頭方向由時差為零的關鍵活動所組成的路線，就稱為關鍵路線。
關鍵路線通常是從始點到終點時間最長的路線，要想縮短整個項目的工期，必須在關鍵路線上想辦法，即縮短關鍵路線上的作業時間。
(二)計劃評審技術(PERT)
計劃評審技術是利用網路順序邏輯關係和加權歷時估算來計算項目歷時的重要技術。它是一種雙代號非肯定型網路分析方法，其理論基礎是假設項目持續時間以及整個項目完成時間是隨機的，且服從某種概率分佈。這種網路計劃方法適用於不可預知因素較多、從未做過的新項目和複雜項目。PERT對各個項目活動的完成時間按三種不同情況估計：樂觀時間——任何事情都順利的情況下完成某項工作的時間；最可能時間——正常情況下完成某項工作的時間。悲觀時間——最不利的情況下完成某項工作的時間。假定三個估計服從β分佈，由此可算出每個活動的期望ti:
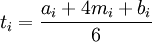
其中：ai表示第i項活動的樂觀時間，mi表示第i項活動的最可能時間，bi表示第i項活動的悲觀時間。根據β分佈的方差計算方法，第i項活動的持續時間方差為:
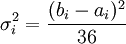
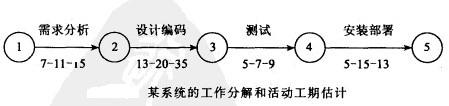
下麵舉例說明。例如，某政府某系統的建設可分解為需求分析、設計編碼、測試和安裝部署四個活動，各個活動順次進行，沒有時間上的重疊，活動的完成時間估計如圖所示。
則各活動的期望工期和方差為：
t需求分析
σ2需求分析
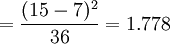
t設計編碼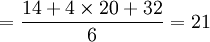
σ2設計編碼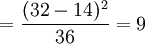
t測試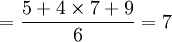
σ2測試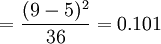
t安裝部署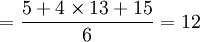
σ2安裝部署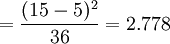
PERT認為整個項目的完成時間是各個活動完成時間之和，且服從正態分佈。整個項目完成的時間t的數學期望T和方差σ2分別等於：
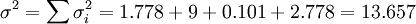
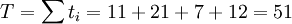
標準差為：
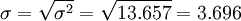天
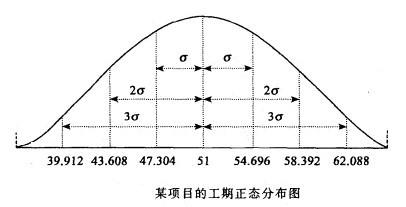
據此，可以得出正態分佈曲線圖：
因為上圖是正態分佈曲線，根據正態分佈規律，在土σ範圍內即在47．304天與54．696天之間完成的概率為68％；在土2σ範圍內完成即在43．608天到58．392天完成的概率為95％；在土3σ範圍內即39．912天到62．088天完成的概率為99％。如果客戶要求在39天內完成，則可完成的概率幾乎為0，也就是說，項目有不可壓縮的最小周期，這是客觀規律。
通過查標準正態分佈表，可得到整個項目在某一時間內完成的概率。例如，如果客戶要求在60天內完成，那麼可能完成的概率為：
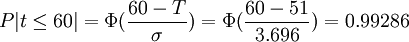
如果客戶要求再提前7天，則完成的概率為：
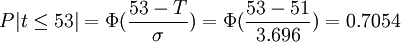
(三)模擬法
模擬法是根據給定的一些假設條件與參數和這些條件與參數發生的概率，運用蒙特卡羅模擬和三角模擬等模擬的方法，模擬確定每個項目活動可能工期的統計分佈和整個項目可能工期的統計分佈，然後使用這些統計數據去編製項目工期計劃的一種方法。
(四)資源調整嘗試法
數學分析法通常產生一個初始進度計劃，而實施這個計劃需要的資源可能比實際擁有的更多，或要求所用資源有大幅度變化。資源調整嘗試法可在資源有約束條件下制定一個進度計劃。用資源調整嘗試法計算出的項目完成時間一般比初始進度長。用電腦優化軟體編製進度計劃時這種方法叫建立在資源約束基礎上的方法。資源有約束的進度編製是資源調整的一個特例，前者涉及的僅是可利用資源在數量上有限制。
(五)甘特圖法
甘特圖法是由美國學者甘特在20世紀初發明的一種最早的項目計劃方法，這種方法是用條形圖表示項目活動及其順序並安排和計劃項目的工期。甘特圖也叫做線條圖或橫道圖，如圖所示。它是以橫線來表示每項活動的起止時間。甘特圖的優點是簡單、明瞭、直觀，易於編製，因此到目前為止仍然是小型項目中常用的工具。即使在大型工程項目中，它也是高級管理層瞭解全局、基層安排進度時有用的工具。在甘特圖上，可以看出各項活動的開始和終了時間。在繪製各項活動的起止時間時，也考慮它們的先後順序，但各項活動之間的關係卻沒有表示出來，同時也沒有指出影響項目壽命周期的關鍵所在。因此，對於複雜的項目來說，甘特圖就顯得不足以適應。
(六)項目管理軟體法
項目管理軟體被廣泛地使用以幫助項目進度的編製。這些軟體可自動進行數學計算和資源凋整，可迅速地對許多方案加以考慮和選擇。用這些軟體，還可列印顯示出計劃編製的結果。
很顯然，採用以上幾種不同的進度計劃方法本身所需的時間和費用是不同的。關鍵日期表編製時間最短，費用最低。甘特圖所需時間要長一些，費用也高一些。CPM要把每個活動都加以分析，如活動數目較多，還需用電腦求出總工期和關鍵路線，因此花費的時間和費用將更多。PERT法可以說是制訂項目進度計劃方法中最複雜的一種，所以花費時間和費用也最多。應該採用哪一種進度計劃方法，主要應考慮下列因素：
1．項目的規模大小。很顯然，小項目應採用簡單的進度計劃方法，大項目為了保證按期按質達到項目目標，就需考慮用較複雜的進度計劃方法。
2．項目的複雜程度。這裡應該註意到，項目的規模並不一定總是與項目的複雜程度成正比。例如修一條公路，規模雖然不小，但並不太複雜，可以用較簡單的進度計劃方法。研製一個小型的電子儀器，則要很複雜的步驟和很多專業知識，可能就需要較複雜的進度計劃方法。
3．項目的緊急性。在項目急需進行時，特別是在開始階段，需要對各項工作發佈指示，以便儘早開始工作，此時，如果用很長時間去編製進度計劃，就會延誤時間。
4．對項目細節掌握的程度。如果在開始階段項目的細節無法明確，CPM和PERT法就無法應用。
5．總進度是否由一、兩項關鍵事項所決定。如果項目進行過程中有一、兩項活動需要花費很長時間，而這期間可把其他準備工作都安排好，那麼對其他工作就不必編製詳細複雜的進度計划了。
6．有無相應的技術力量和設備。例如，沒有電腦，CPM和PERT進度計劃方法有時就難以應用。如果沒有受過良好訓練的合格的技術人員，也無法勝任用複雜的方法編製進度計劃。此外，根據情況不同，還需考慮客戶的要求，能夠用在進度計划上的預算等因素。到底採用哪一種方法來編製進度計劃，要全面考慮以上各個因素。
項目時間計劃的編製結果[3]
(一)項目進度計劃書
通過項目時間計劃編製而給出的項目時間計劃書，至少應包括項目整體和每項活動的計劃開始時間和計劃結束時間等信息。一般在項目資源配置得到確認之前，這種項目時間計劃只是初步計劃；在項目資源配置得到確認之後，才能得到正式的項目時間計劃。項目時間計劃可以使用文字描述的形式給出，也可以使用圖表的形式給出。例如表就是一種用里程碑表的形式給出的項目時間計劃書。
| 時間 | 一月 | 二月 | 三月 | 四月 | 五月 | 六月 | 七月 | 八月 |
| A | △ ▼ | |||||||
| B | ▽ | |||||||
| C | △ | |||||||
| D | △ | |||||||
| E | △ | |||||||
| F | △ |
(二)詳細說明
項目進度的詳細說明要包括對所有假設和約束條件的說明和具體實施計劃的措施說明等。詳細依據的數量因應用領域而異。例如，在建築項目中，它可能包括資源柱狀圖、現金流預測以及訂貨和交貨時間表。在電子項目中，它可能只包括資源柱狀圖。詳細說明提供的信息通常包括：按時段提出的資源需求，替代進度計劃以及進度儲備或進度風險估算。
(三)進度管理計劃
項目進度管理計劃是說明對進度的變化應如何加以變更和如何開展項目時間控制的計劃安排。根據實際需要，進度管理計劃可做得非常詳細也可粗框架，可用正規形式也可以非正規形式表示。但無論採取什麼方式，它都是整個項目計劃的一部分。
(四)資源需求的修改
在項目時間計劃編製中，資源調整和活動目錄的修改可能對資源的初始估計產生很大的影響，往往會出現對於項目資源需求的各種調整和改動。因此，在項目時間計劃的制定過程中，需要對所有的項目資源需求調整和改動進行必要的管理，並編製一份更新後的項目資源需求文件。
