项目时间计划
出自 MBA智库百科(https://wiki.mbalib.com/)
目录 |
什么是项目时间计划[1]
项目时间计划是对项目所有活动的顺序和工期进行安排、协调，并确定项目的总工期。最终的进度计划通常要放在日历表上。
项目时间计划的依据[2]
项目时间计划的详细依据是对所有可识别的假设和限制的文件化。这种附加细节到底应该有多少取决于项目的特点和要求，例如在建设项目中，最可能包含资源柱状图、现金流计划以及预制和交付的时间计划等事项；而在电子项目中，很可能只包含资源柱状图。通常情况下，作为详细依据适用的信息包括：
1．随时间进度而改变的资源需求，通常以资源柱状图的形式来显示。
2．可替代的时间计划，如最好的或最坏的情况，带有或不带有强制要求的资源等。
3．进度储备或进度风险评估。
项目时间计划的制定[3]
制定项目时间计划是为了控制时间和节约时间，而项目一般都具有严格的时间要求，因此使得时间计划在项目管理中变得很重要。项目时间计划是在工作分解结构的基础上对活动、项目做出的一系列的时间计划，它主要说明哪些工作必须于何时完成，以及完成每一项任务所需要的时间，有时也表示出每项活动所需的人数。
一、项目进度计划的时间参数
项目进度计划记录了项目中每一活动的计划和实际的开始日期、完成日期和周期。在大多数复杂的进度计划中，都会用到下列时间参数以及相关的时间参数：
(一)工期
工期是完成活动所需的时间。在每个活动开始之前，都有一个估算的周期，而在每个活动开始之后完成之前，我们也可以估算剩余周期。一旦活动已经完成，我们就可以记录实际周期。
(二)最早开始时间(ES)和最早结束时间(EF)
最早开始时间是指某项活动能够开始的最早时间。它可以在项目的预计开始时间和所有正常的工期估计基础上计算出来。最早结束时间是指某一活动能够完成的最早时间，它可以在这项活动最早开始时间的基础上加上这项活动的工期估计计算出来。
EF=ES+工期估计
(三)最迟开始时间(LS)和最迟结束时间(LF)
最迟开始时间是指为了使项目在要求完工的时间内完成，某项活动必须开始的最迟时间。最迟结束时间是指为了使项目在完工时间内完成，某项活动必须完成的最迟时间。它可以在项目的要求完工时间和各项紧随活动工期估计的基础上计算出来。最迟开始时间可以用这项活动的最迟结束时间减去它的工期估算计算出来。
LS=LF-工期估计
(四)时差
如果最迟开始时间与最早开始时间不同，那么该活动的开始时间就可以浮动，称之为时差：
时差=最迟开始时间-最早开始时间
同理，如果最迟结束时间和最早结束时间不同，那么该活动的结束时间也可以浮动，同样称为该活动的时差：
时差=最迟结束时间-最早结束时间
二、编制项目时间计划的方法与工具
(一)关键路线法(CPM)
关键路线法(CPM)是一种常用的数学分析技术，是根据网络图和各活动所需时间(估计值)，计算每一活动的最早或最迟开始和结束时间。但计算时并没有考虑资源限制，这样算出的日期并不是实际进度，而是表示所需的时间长短，考虑活动的资源限制和其他约束条件，把活动安排在上述时间区间内。在计算出作业时间、节点时间和活动时间后，结合考虑时差，可以求出项目的关键路线。关键路线法(CPM)的关键是计算总时差，这样可决定哪一活动有最小时间弹性。CPM算法也在其他类型的数学分析中得到应用。CPM算法的具体步骤如下：
1．求出各活动的ES和EF。我们可以通过公式求出各活动的时间参数ES和EF，这是通过正向计算得到的。即从项目开始沿网络图到项目完成进行计算。在进行这些正向计算时必须注意：某项活动的最早开始时间必须相同或晚于直接指向这一活动的所有活动的最早结束时间中的最晚时间。
2．求出各活动的LF和LS。计算各活动的LF和LS，可以通过反向推算得出。即从项目完成沿网络图到项目的开始进行推算。在进行这类推算时也必须注意：某项活动的最迟结束时间必须相同或者早于该活动直接指向的所有活动最迟开始时间的最早时间。
3．计算时差。要分别计算出活动总时差和每项工作活动的单时差。活动总时差是指在不影响整个项目完工时间的条件下，某项活动最迟开始时间与最早开始时间的差。它表明该活动开始时间允许推迟的最大限度。活动单时差是指在不影响下一活动的最早开始时间的前提下，该活动完工期可能有的机动时间。
4．找出关键路线。在一个网络图中，总时差为零的活动，称为关键活动。时差为零的节点称为关键节点。一个从始点到终点，沿箭头方向由时差为零的关键活动所组成的路线，就称为关键路线。
关键路线通常是从始点到终点时间最长的路线，要想缩短整个项目的工期，必须在关键路线上想办法，即缩短关键路线上的作业时间。
(二)计划评审技术(PERT)
计划评审技术是利用网络顺序逻辑关系和加权历时估算来计算项目历时的重要技术。它是一种双代号非肯定型网络分析方法，其理论基础是假设项目持续时间以及整个项目完成时间是随机的，且服从某种概率分布。这种网络计划方法适用于不可预知因素较多、从未做过的新项目和复杂项目。PERT对各个项目活动的完成时间按三种不同情况估计：乐观时间——任何事情都顺利的情况下完成某项工作的时间；最可能时间——正常情况下完成某项工作的时间。悲观时间——最不利的情况下完成某项工作的时间。假定三个估计服从β分布，由此可算出每个活动的期望ti:
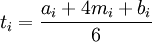
其中：ai表示第i项活动的乐观时间，mi表示第i项活动的最可能时间，bi表示第i项活动的悲观时间。根据β分布的方差计算方法，第i项活动的持续时间方差为:
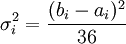
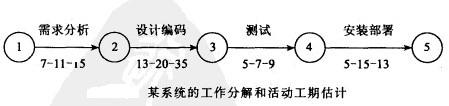
下面举例说明。例如，某政府某系统的建设可分解为需求分析、设计编码、测试和安装部署四个活动，各个活动顺次进行，没有时间上的重叠，活动的完成时间估计如图所示。
则各活动的期望工期和方差为：
t需求分析
σ2需求分析
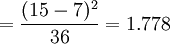
t设计编码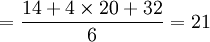
σ2设计编码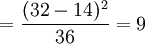
t测试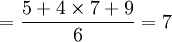
σ2测试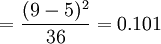
t安装部署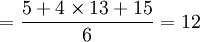
σ2安装部署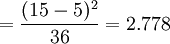
PERT认为整个项目的完成时间是各个活动完成时间之和，且服从正态分布。整个项目完成的时间t的数学期望T和方差σ2分别等于：
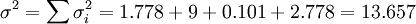
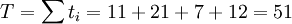
标准差为：
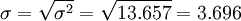天
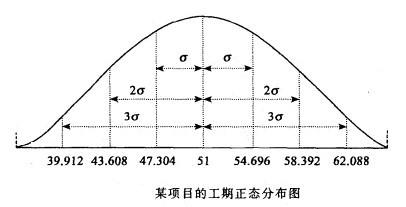
据此，可以得出正态分布曲线图：
因为上图是正态分布曲线，根据正态分布规律，在土σ范围内即在47．304天与54．696天之间完成的概率为68％；在土2σ范围内完成即在43．608天到58．392天完成的概率为95％；在土3σ范围内即39．912天到62．088天完成的概率为99％。如果客户要求在39天内完成，则可完成的概率几乎为0，也就是说，项目有不可压缩的最小周期，这是客观规律。
通过查标准正态分布表，可得到整个项目在某一时间内完成的概率。例如，如果客户要求在60天内完成，那么可能完成的概率为：
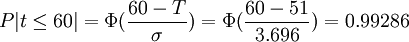
如果客户要求再提前7天，则完成的概率为：
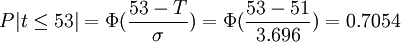
(三)模拟法
模拟法是根据给定的一些假设条件与参数和这些条件与参数发生的概率，运用蒙特卡罗模拟和三角模拟等仿真的方法，模拟确定每个项目活动可能工期的统计分布和整个项目可能工期的统计分布，然后使用这些统计数据去编制项目工期计划的一种方法。
(四)资源调整尝试法
数学分析法通常产生一个初始进度计划，而实施这个计划需要的资源可能比实际拥有的更多，或要求所用资源有大幅度变化。资源调整尝试法可在资源有约束条件下制定一个进度计划。用资源调整尝试法计算出的项目完成时间一般比初始进度长。用计算机优化软件编制进度计划时这种方法叫建立在资源约束基础上的方法。资源有约束的进度编制是资源调整的一个特例，前者涉及的仅是可利用资源在数量上有限制。
(五)甘特图法
甘特图法是由美国学者甘特在20世纪初发明的一种最早的项目计划方法，这种方法是用条形图表示项目活动及其顺序并安排和计划项目的工期。甘特图也叫做线条图或横道图，如图所示。它是以横线来表示每项活动的起止时间。甘特图的优点是简单、明了、直观，易于编制，因此到目前为止仍然是小型项目中常用的工具。即使在大型工程项目中，它也是高级管理层了解全局、基层安排进度时有用的工具。在甘特图上，可以看出各项活动的开始和终了时间。在绘制各项活动的起止时间时，也考虑它们的先后顺序，但各项活动之间的关系却没有表示出来，同时也没有指出影响项目寿命周期的关键所在。因此，对于复杂的项目来说，甘特图就显得不足以适应。
(六)项目管理软件法
项目管理软件被广泛地使用以帮助项目进度的编制。这些软件可自动进行数学计算和资源凋整，可迅速地对许多方案加以考虑和选择。用这些软件，还可打印显示出计划编制的结果。
很显然，采用以上几种不同的进度计划方法本身所需的时间和费用是不同的。关键日期表编制时间最短，费用最低。甘特图所需时间要长一些，费用也高一些。CPM要把每个活动都加以分析，如活动数目较多，还需用计算机求出总工期和关键路线，因此花费的时间和费用将更多。PERT法可以说是制订项目进度计划方法中最复杂的一种，所以花费时间和费用也最多。应该采用哪一种进度计划方法，主要应考虑下列因素：
1．项目的规模大小。很显然，小项目应采用简单的进度计划方法，大项目为了保证按期按质达到项目目标，就需考虑用较复杂的进度计划方法。
2．项目的复杂程度。这里应该注意到，项目的规模并不一定总是与项目的复杂程度成正比。例如修一条公路，规模虽然不小，但并不太复杂，可以用较简单的进度计划方法。研制一个小型的电子仪器，则要很复杂的步骤和很多专业知识，可能就需要较复杂的进度计划方法。
3．项目的紧急性。在项目急需进行时，特别是在开始阶段，需要对各项工作发布指示，以便尽早开始工作，此时，如果用很长时间去编制进度计划，就会延误时间。
4．对项目细节掌握的程度。如果在开始阶段项目的细节无法明确，CPM和PERT法就无法应用。
5．总进度是否由一、两项关键事项所决定。如果项目进行过程中有一、两项活动需要花费很长时间，而这期间可把其他准备工作都安排好，那么对其他工作就不必编制详细复杂的进度计划了。
6．有无相应的技术力量和设备。例如，没有计算机，CPM和PERT进度计划方法有时就难以应用。如果没有受过良好训练的合格的技术人员，也无法胜任用复杂的方法编制进度计划。此外，根据情况不同，还需考虑客户的要求，能够用在进度计划上的预算等因素。到底采用哪一种方法来编制进度计划，要全面考虑以上各个因素。
项目时间计划的编制结果[3]
(一)项目进度计划书
通过项目时间计划编制而给出的项目时间计划书，至少应包括项目整体和每项活动的计划开始时间和计划结束时间等信息。一般在项目资源配置得到确认之前，这种项目时间计划只是初步计划；在项目资源配置得到确认之后，才能得到正式的项目时间计划。项目时间计划可以使用文字描述的形式给出，也可以使用图表的形式给出。例如表就是一种用里程碑表的形式给出的项目时间计划书。
| 时间 | 一月 | 二月 | 三月 | 四月 | 五月 | 六月 | 七月 | 八月 |
| A | △ ▼ | |||||||
| B | ▽ | |||||||
| C | △ | |||||||
| D | △ | |||||||
| E | △ | |||||||
| F | △ |
(二)详细说明
项目进度的详细说明要包括对所有假设和约束条件的说明和具体实施计划的措施说明等。详细依据的数量因应用领域而异。例如，在建筑项目中，它可能包括资源柱状图、现金流预测以及订货和交货时间表。在电子项目中，它可能只包括资源柱状图。详细说明提供的信息通常包括：按时段提出的资源需求，替代进度计划以及进度储备或进度风险估算。
(三)进度管理计划
项目进度管理计划是说明对进度的变化应如何加以变更和如何开展项目时间控制的计划安排。根据实际需要，进度管理计划可做得非常详细也可粗框架，可用正规形式也可以非正规形式表示。但无论采取什么方式，它都是整个项目计划的一部分。
(四)资源需求的修改
在项目时间计划编制中，资源调整和活动目录的修改可能对资源的初始估计产生很大的影响，往往会出现对于项目资源需求的各种调整和改动。因此，在项目时间计划的制定过程中，需要对所有的项目资源需求调整和改动进行必要的管理，并编制一份更新后的项目资源需求文件。
