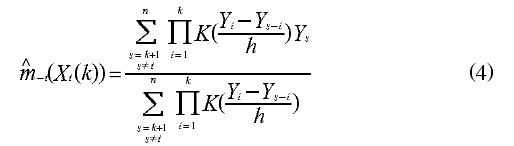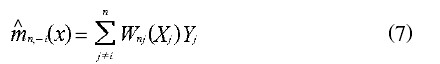非參數自回歸預測模型
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
非參數自回歸預測模型的原理[1]
採用非參數自回歸模型對平穩時間序列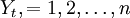 進行分析並預測
進行分析並預測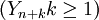 的值的建模步驟如下:
的值的建模步驟如下:
(1)對經過小波分解和重構後的各個分層繫數建立相應的非參數自回歸模型
Yt = m(Xt)et (2)
式(2)稱作非參數自回歸模型。未知函數 稱為自回歸函數。
稱為自回歸函數。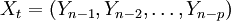 為解釋變數,它是影響變數Y的p個因素(為正整數)。其中,et稱為均值為零隨機誤差序列且獨立同分佈,且
為解釋變數,它是影響變數Y的p個因素(為正整數)。其中,et稱為均值為零隨機誤差序列且獨立同分佈,且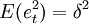 ,它反映了除解釋變數,存在其它影響被解釋變數的可獲知或不可獲知的因素。從隨機誤差序列滿足的條件看出,et之間互不相關,且et與以前的觀測值也互不相關。
,它反映了除解釋變數,存在其它影響被解釋變數的可獲知或不可獲知的因素。從隨機誤差序列滿足的條件看出,et之間互不相關,且et與以前的觀測值也互不相關。
(2)採用非參數分析的方法估計上述模型中的 ,記作
,記作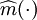 。
。
(3)根據建立的模型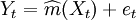 對未知參數值Yn + k進行非參數預測。
對未知參數值Yn + k進行非參數預測。
非參數自回歸預測模型的建立[1]
1.模型階數的選擇
對於模型階數p值的確定,採用Cheng和Tong相合的定階方法即Cross-Validation方法來確定的p值。其核心思想如下:原始樣本數據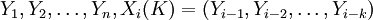 ,首先假定模型(2)的階數的上界L{1,2,…,L},分別計算,如式(3)所示。其中,使式(3)達到極小的值即為模型階數p的估計值
,首先假定模型(2)的階數的上界L{1,2,…,L},分別計算,如式(3)所示。其中,使式(3)達到極小的值即為模型階數p的估計值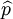 滿足A。其中
滿足A。其中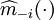 表示除去第i個數據後,剩餘樣本數據對自回歸參數
表示除去第i個數據後,剩餘樣本數據對自回歸參數 的核估計,如式(4)。式中:
的核估計,如式(4)。式中:
註釋上式中A表示如下圖
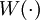 ——適當選取的非負權函數,
——適當選取的非負權函數,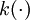 ——自選核函數。
——自選核函數。
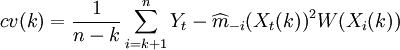 (3)
(3)
2.自回歸函數 的估計
的估計
如何對模型(2)的進行估計,方法有很多種。下麵介紹局部線性估計方法。已經證明,局部線性估計在邊界點的收斂速度與內點的一樣且其偏差與解釋變數的密度函數也無關,即與核估計不同,其不存在邊界效應問題。除此之外,局部線性估計可同時估計出函數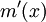 和回歸函數的導函數。
和回歸函數的導函數。
局部線性估計即為式(5)。
![\min{\sum_{i=1}^n[Y_i-m(x)-m^\prime(x)(X_i-x)]^2K_h(X_i-x)}](/w/images/math/8/d/4/8d42b3d9340df90c9539d7875afe20bd.png) (5)
(5)
式中: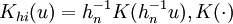 為概率密度函數。
為概率密度函數。
Yi = m(x) + m(x)(Xi − x) + ei(6)
3.窗寬的選擇
交錯鑒定方法是選擇窗寬的一個常用方法,其基本思路是:在某個局部觀測值x = Xi,首先,在樣本中剔除該觀測值(Xi,Yi)坐標,,而後對其餘的n-1個點在x = Xi處作核估計。
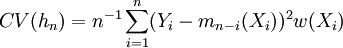 (8)
(8)
稱作為平方擬合誤差。使最小的窗寬,則是最佳的窗寬hn,其中w(x)≥0為某權數。
該方法的關鍵是在樣本中剔除觀測值點(Xi,Yi)。如果不這樣,由於核權函數W_{ni}在觀測點x = Xi達到最大值,就會使得x = Xi重要程度過分誇大而其它觀測點數據的重要程度降低。
所以採用交錯鑒定方法避免了因為沒有剔除觀測點(Xi,Yi)而將有用的數據排除在外的情況。
基於交錯鑒定選擇窗寬的過程方法,採用交錯鑒定法來確定最優窗寬。
4.模型預測
模型預測一般採用直接預測法,但直接預測法並沒有包含新預測值的信息。為了提高預測精度,利用迴圈預測法進行預測。此預測方法的原理就是迴圈再利用一步向前的預測值。其主旨是:當預測得到Yn + i時,把Yn + i − 1預測值添加到原始樣本序列組成新的時間序列。對新序列採用上述非參數自回歸預測方法得到新的預測值Yn + i,依次迴圈,得到所需要的預測值。
國民收入的非參數自回歸預測模型[1]
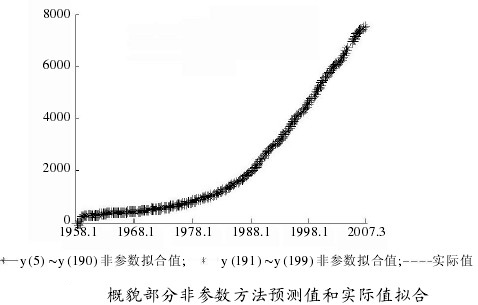
程式在Matlab軟體中實現用Db10對原始信號進行3層分解和重構,然後對重構後的細節信號和概貌信號用非參數自回歸預測方法分別進行分析預測,這些分支時間序列預測結果的和便是原始序列的預測結果。原始數據是1958-2007年某國國民收入季度數據。預測的方法是根據前190個數據(1958.1-2005.2)來預測2005.3-2007.3的9個季度的數據。
在此只介紹概貌部分的預測過程。先對概貌部分時間序列建立參數自回歸預測模型:使用準則確定的階數為4階,AIC=-15.7956。AR(4)模型如式(9)表示。式(9)中模型參數是用最小二乘方法求得的。再對概貌部分建立非參數自回歸預測模型:如式(10)。其中,隨機誤差序列et獨立同分佈,此隨機誤差序列均值為零,均方差為σ2且et與 相互獨立。選用高斯核函數=1
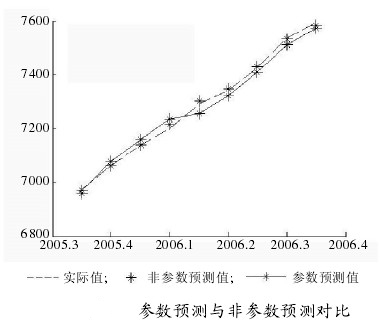
相互獨立。選用高斯核函數=1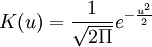 ,窗寬h=1.56。利用Matlab編程求得最小cv(k)值即cv(1),模型的階次為1階,此時非參數自回歸模型為式(11)。利用此模型以概貌部分的前190個數據為樣本,預測後9個數據,如上圖所示。同理,對細節部分d3,d2,d1時間序列利用非參數方法進行預測,所求預測結果便是概貌部分和細節部分之和。並使參數預測方法和非參數預測方法相比較,如下圖所示。
,窗寬h=1.56。利用Matlab編程求得最小cv(k)值即cv(1),模型的階次為1階,此時非參數自回歸模型為式(11)。利用此模型以概貌部分的前190個數據為樣本,預測後9個數據,如上圖所示。同理,對細節部分d3,d2,d1時間序列利用非參數方法進行預測,所求預測結果便是概貌部分和細節部分之和。並使參數預測方法和非參數預測方法相比較,如下圖所示。
Yi = 1.3716Yi − 1 − 0.3922Yi − 2 − 0.02422Yi − 3 − 0.1696Yi − 4(9)
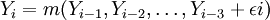 (10)
(10)
Yi = m(Yi − 1 + εi(11)
從下表中可以看出非參數自回歸預測的MAE即平均絕對誤差和MSE即均方誤差都比用參數自回歸的平均絕對誤差和均方誤差要小。可見用前者比後者更能體現數據的趨勢發展。
| 參數預測方法 | 非參數預測方法 | |
| MAE | 22.6778 | 7.6449 |
| MSE | 7.5667 | 2.9960 |
利用小波分解與重構和非參數自回歸模型相結合分析的方法來對數據進行分析,同時與小波分解後,用參數自回歸模型進行分析的方法進行了比較。利用參數自回歸模型進行分析的時候,往往需要假定產生數據的總體分佈的形式是已知的。所不能確定的是數量有限的一些參數值,而所要做的就是對這些參數進行估計或檢驗。但是在實踐中,在沒有足夠證據的時候去假設一個總體具有某種分佈形式,併進行參數估計或檢驗是不負責的,結果是不可靠的。非參數統計就是對總體分佈形式不瞭解時進行推斷的統計方法。所以非參數方法相比參數自回歸模型分析方法有很好的穩健性。
利用非參數自回歸模型和參數自回歸模型對2005.3-2007.3的國民收入總值分別進行預測。結果如下表所示。可以明顯看出,表2中比起用參數自回歸模型得到的預測結果,非參數自回歸模型所得到的2005.3-2007.3季度數據預測值更接近原始數據。建立的非參數自回歸模型是有效的。綜上所述,非參數自回歸模型在本文國民收入建模預測的問題上,比起參數自回歸模型更合適更有效。
| 季度 | 實際值(萬元) | 參數自回歸預測值(萬元) | 非參數自回歸預測值(萬元) |
| 2005.3 | 6977.6 | 6970.9 | 6961.5 |
| 2005.4 | 7062.2 | 7080.2 | 7063.1 |
| 2006.1 | 7140.5 | 7160.9 | 7136.7 |
| 2006.2 | 7202.4 | 7234.5 | 7213.3 |
| 2006.3 | 7293.4 | 7253.6 | 7303.1 |
| 2006.4 | 7344.3 | 7321.6 | 7348.7 |
| 2007.1 | 7426.6 | 7410.5 | 7431.2 |
| 2007.2 | 7537.5 | 7511.9 | 7531.9 |
| 2007.3 | 7593.6 | 7570.9 | 7580.6 |