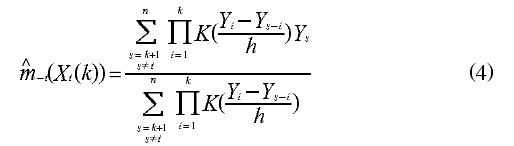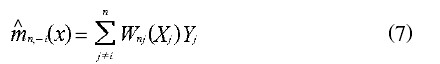非参数自回归预测模型
出自 MBA智库百科(https://wiki.mbalib.com/)
目录 |
非参数自回归预测模型的原理[1]
采用非参数自回归模型对平稳时间序列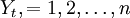 进行分析并预测
进行分析并预测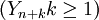 的值的建模步骤如下:
的值的建模步骤如下:
(1)对经过小波分解和重构后的各个分层系数建立相应的非参数自回归模型
Yt = m(Xt)et (2)
式(2)称作非参数自回归模型。未知函数 称为自回归函数。
称为自回归函数。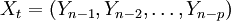 为解释变量,它是影响变量Y的p个因素(为正整数)。其中,et称为均值为零随机误差序列且独立同分布,且
为解释变量,它是影响变量Y的p个因素(为正整数)。其中,et称为均值为零随机误差序列且独立同分布,且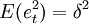 ,它反映了除解释变量,存在其它影响被解释变量的可获知或不可获知的因素。从随机误差序列满足的条件看出,et之间互不相关,且et与以前的观测值也互不相关。
,它反映了除解释变量,存在其它影响被解释变量的可获知或不可获知的因素。从随机误差序列满足的条件看出,et之间互不相关,且et与以前的观测值也互不相关。
(2)采用非参数分析的方法估计上述模型中的 ,记作
,记作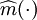 。
。
(3)根据建立的模型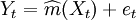 对未知参数值Yn + k进行非参数预测。
对未知参数值Yn + k进行非参数预测。
非参数自回归预测模型的建立[1]
1.模型阶数的选择
对于模型阶数p值的确定,采用Cheng和Tong相合的定阶方法即Cross-Validation方法来确定的p值。其核心思想如下:原始样本数据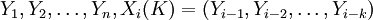 ,首先假定模型(2)的阶数的上界L{1,2,…,L},分别计算,如式(3)所示。其中,使式(3)达到极小的值即为模型阶数p的估计值
,首先假定模型(2)的阶数的上界L{1,2,…,L},分别计算,如式(3)所示。其中,使式(3)达到极小的值即为模型阶数p的估计值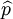 满足A。其中
满足A。其中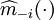 表示除去第i个数据后,剩余样本数据对自回归参数
表示除去第i个数据后,剩余样本数据对自回归参数 的核估计,如式(4)。式中:
的核估计,如式(4)。式中:
注释上式中A表示如下图
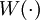 ——适当选取的非负权函数,
——适当选取的非负权函数,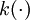 ——自选核函数。
——自选核函数。
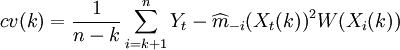 (3)
(3)
2.自回归函数 的估计
的估计
如何对模型(2)的进行估计,方法有很多种。下面介绍局部线性估计方法。已经证明,局部线性估计在边界点的收敛速度与内点的一样且其偏差与解释变量的密度函数也无关,即与核估计不同,其不存在边界效应问题。除此之外,局部线性估计可同时估计出函数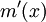 和回归函数的导函数。
和回归函数的导函数。
局部线性估计即为式(5)。
![\min{\sum_{i=1}^n[Y_i-m(x)-m^\prime(x)(X_i-x)]^2K_h(X_i-x)}](/w/images/math/8/d/4/8d42b3d9340df90c9539d7875afe20bd.png) (5)
(5)
式中: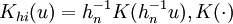 为概率密度函数。
为概率密度函数。
Yi = m(x) + m(x)(Xi − x) + ei(6)
3.窗宽的选择
交错鉴定方法是选择窗宽的一个常用方法,其基本思路是:在某个局部观测值x = Xi,首先,在样本中剔除该观测值(Xi,Yi)坐标,,而后对其余的n-1个点在x = Xi处作核估计。
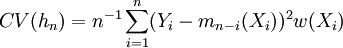 (8)
(8)
称作为平方拟合误差。使最小的窗宽,则是最佳的窗宽hn,其中w(x)≥0为某权数。
该方法的关键是在样本中剔除观测值点(Xi,Yi)。如果不这样,由于核权函数W_{ni}在观测点x = Xi达到最大值,就会使得x = Xi重要程度过分夸大而其它观测点数据的重要程度降低。
所以采用交错鉴定方法避免了因为没有剔除观测点(Xi,Yi)而将有用的数据排除在外的情况。
基于交错鉴定选择窗宽的过程方法,采用交错鉴定法来确定最优窗宽。
4.模型预测
模型预测一般采用直接预测法,但直接预测法并没有包含新预测值的信息。为了提高预测精度,利用循环预测法进行预测。此预测方法的原理就是循环再利用一步向前的预测值。其主旨是:当预测得到Yn + i时,把Yn + i − 1预测值添加到原始样本序列组成新的时间序列。对新序列采用上述非参数自回归预测方法得到新的预测值Yn + i,依次循环,得到所需要的预测值。
国民收入的非参数自回归预测模型[1]
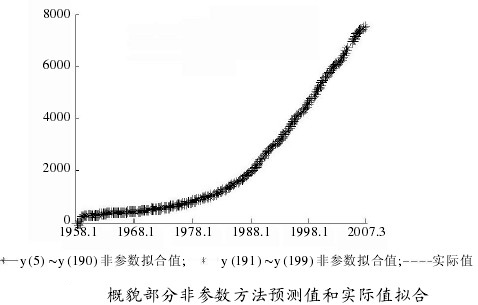
程序在Matlab软件中实现用Db10对原始信号进行3层分解和重构,然后对重构后的细节信号和概貌信号用非参数自回归预测方法分别进行分析预测,这些分支时间序列预测结果的和便是原始序列的预测结果。原始数据是1958-2007年某国国民收入季度数据。预测的方法是根据前190个数据(1958.1-2005.2)来预测2005.3-2007.3的9个季度的数据。
在此只介绍概貌部分的预测过程。先对概貌部分时间序列建立参数自回归预测模型:使用准则确定的阶数为4阶,AIC=-15.7956。AR(4)模型如式(9)表示。式(9)中模型参数是用最小二乘方法求得的。再对概貌部分建立非参数自回归预测模型:如式(10)。其中,随机误差序列et独立同分布,此随机误差序列均值为零,均方差为σ2且et与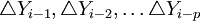 相互独立。选用高斯核函数=1
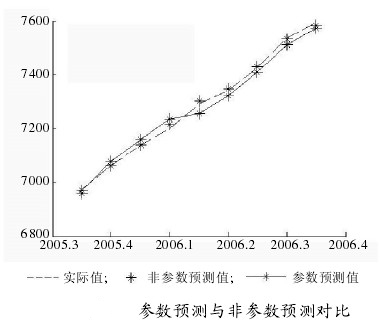
相互独立。选用高斯核函数=1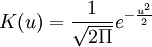 ,窗宽h=1.56。利用Matlab编程求得最小cv(k)值即cv(1),模型的阶次为1阶,此时非参数自回归模型为式(11)。利用此模型以概貌部分的前190个数据为样本,预测后9个数据,如上图所示。同理,对细节部分d3,d2,d1时间序列利用非参数方法进行预测,所求预测结果便是概貌部分和细节部分之和。并使参数预测方法和非参数预测方法相比较,如下图所示。
,窗宽h=1.56。利用Matlab编程求得最小cv(k)值即cv(1),模型的阶次为1阶,此时非参数自回归模型为式(11)。利用此模型以概貌部分的前190个数据为样本,预测后9个数据,如上图所示。同理,对细节部分d3,d2,d1时间序列利用非参数方法进行预测,所求预测结果便是概貌部分和细节部分之和。并使参数预测方法和非参数预测方法相比较,如下图所示。
Yi = 1.3716Yi − 1 − 0.3922Yi − 2 − 0.02422Yi − 3 − 0.1696Yi − 4(9)
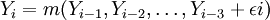 (10)
(10)
Yi = m(Yi − 1 + εi(11)
从下表中可以看出非参数自回归预测的MAE即平均绝对误差和MSE即均方误差都比用参数自回归的平均绝对误差和均方误差要小。可见用前者比后者更能体现数据的趋势发展。
| 参数预测方法 | 非参数预测方法 | |
| MAE | 22.6778 | 7.6449 |
| MSE | 7.5667 | 2.9960 |
利用小波分解与重构和非参数自回归模型相结合分析的方法来对数据进行分析,同时与小波分解后,用参数自回归模型进行分析的方法进行了比较。利用参数自回归模型进行分析的时候,往往需要假定产生数据的总体分布的形式是已知的。所不能确定的是数量有限的一些参数值,而所要做的就是对这些参数进行估计或检验。但是在实践中,在没有足够证据的时候去假设一个总体具有某种分布形式,并进行参数估计或检验是不负责的,结果是不可靠的。非参数统计就是对总体分布形式不了解时进行推断的统计方法。所以非参数方法相比参数自回归模型分析方法有很好的稳健性。
利用非参数自回归模型和参数自回归模型对2005.3-2007.3的国民收入总值分别进行预测。结果如下表所示。可以明显看出,表2中比起用参数自回归模型得到的预测结果,非参数自回归模型所得到的2005.3-2007.3季度数据预测值更接近原始数据。建立的非参数自回归模型是有效的。综上所述,非参数自回归模型在本文国民收入建模预测的问题上,比起参数自回归模型更合适更有效。
| 季度 | 实际值(万元) | 参数自回归预测值(万元) | 非参数自回归预测值(万元) |
| 2005.3 | 6977.6 | 6970.9 | 6961.5 |
| 2005.4 | 7062.2 | 7080.2 | 7063.1 |
| 2006.1 | 7140.5 | 7160.9 | 7136.7 |
| 2006.2 | 7202.4 | 7234.5 | 7213.3 |
| 2006.3 | 7293.4 | 7253.6 | 7303.1 |
| 2006.4 | 7344.3 | 7321.6 | 7348.7 |
| 2007.1 | 7426.6 | 7410.5 | 7431.2 |
| 2007.2 | 7537.5 | 7511.9 | 7531.9 |
| 2007.3 | 7593.6 | 7570.9 | 7580.6 |