平均指標
出自 MBA智库百科(https://wiki.mbalib.com/)
平均指標(Average Indicators)
目錄 |
平均指標又稱“統計平均數”,用以反映社會經濟現象總體各單位某一數量標誌在一定時間、地點條件下所達到的一般水平的綜合指標。
平均指標的種類有:算術平均數、調和平均數、幾何平均數、眾數和中位數。前三種平均數是根據總體所有標誌值計算的所以稱為數值平均數,後兩種平均數是根據標誌值所處的位置確定的,因此稱為位置平均數。
1、算術平均數的計算
算術平均數是計算平均指標的最常用方法,它的基本公式形式是總體標誌總量除以總體單位總量。在實際工作中,由於資料的不同,算術平均數有兩種計算形式:即簡單算術平均數和加權算術平均數。
簡單算術平均數:
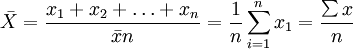
其中:---  算術平均數,X---各單位標誌值(變數值),n---總體單位數(項數)。
算術平均數,X---各單位標誌值(變數值),n---總體單位數(項數)。
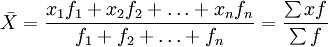
其中: ----代表算術平均數,x 代表各單位標誌值(變數值),f 代表各組單位數(項數)。
----代表算術平均數,x 代表各單位標誌值(變數值),f 代表各組單位數(項數)。
簡單算術平均數適用於未分組的統計資料,如果已知各單位標誌值和總體單位數,可採用簡單算術平均數方法計算。
加權算術平均數適用於分組的統計資料,如果已知各組的變數值和變數值出現的次數,則可採用加權算術平均數計算。在“加權算術平均數=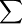 (各組變數值×各組次數)/
(各組變數值×各組次數)/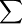 各組次數”,公式中,各組次數具有權衡各組變數值輕重的作用,某一組的次數越大,則該組的變數值對平均數的影響就越大,反之越小。加權算術平均數的大小受兩個因素的影響,其一是受變數值大小的影響。其二是受次數分配值即各組次數占總次數比重的影響。加權算術平均數中的權數,指的就是標誌值出現的次數或各組次數占總次數的比重。在計算平均數時,由於出現次數多的標誌值對平均數的形成影響大些,出現次數少的標誌值對平均數的形成影響小些,因此就把次數稱為權數。在分組數列的條件下,當各組標誌值出現的次數或各組次數所占比重均相等時,權數就失去了權衡輕重的作用,這時用加權算術平均數計算的結果與用簡單算術平均數計算的結果相同。
各組次數”,公式中,各組次數具有權衡各組變數值輕重的作用,某一組的次數越大,則該組的變數值對平均數的影響就越大,反之越小。加權算術平均數的大小受兩個因素的影響,其一是受變數值大小的影響。其二是受次數分配值即各組次數占總次數比重的影響。加權算術平均數中的權數,指的就是標誌值出現的次數或各組次數占總次數的比重。在計算平均數時,由於出現次數多的標誌值對平均數的形成影響大些,出現次數少的標誌值對平均數的形成影響小些,因此就把次數稱為權數。在分組數列的條件下,當各組標誌值出現的次數或各組次數所占比重均相等時,權數就失去了權衡輕重的作用,這時用加權算術平均數計算的結果與用簡單算術平均數計算的結果相同。
2、調和平均數的計算
在實際工作中,有時由於缺乏總體的單位數資料,而不能直接計算平均數,這時就可採用調和平均數計算。因此在統計工作中,調和平均數常常被作為算術平均數的變形來使用。調和平均數也有簡單調和平均數和加權調和平均數兩種形式。
例2、某月某企業按工人勞動生產率高低分組的生產班組數和產量資料如下:
| 按工人勞動生產率 分組(件/人) | 生產班組 | 產量(件) |
|---|---|---|
| 50-60 60-70 70-80 80-90 90以上 | 10 7 5 2 1 | 8250 6500 5250 2550 1520 |
試計算該企業工人平均勞動生產率。
解:列計算表如下:
| 按工人勞動生產率 分組(件/人) | 組中值 | 產量(件) | 人數 |
|---|---|---|---|
| 50-60 60-70 70-80 80-90 90以上 | 55 65 75 85 95 | 8250 6500 5250 2550 1520 | 150 100 70 30 16 |
| 合 計 | 24070 | 366 |
工人平均勞動生產率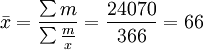 (件/人)
(件/人)
註意本題計算中權數的選擇。資料中“生產班組”可以是次數,但並不是合適的權數。因為本題中的工人勞動生產率是按件/人計算的,和生產班組沒有直接關係,所以它不能作為權數進行平均數的計算。本題應以“產量”權數,進行加權調和平均數的計算。
加權算術平均數與加權調和平均數是計算平均指標時常常用到的兩個指標。加權算術平均數中的權數一般情況下是資料已經分組得出分配數列的情況下標誌值的次數。而加權調和平均數的權數是直接給定的標誌總量。在經濟統計中,經常因為無法直接得到被平均標誌值的相應次數的資料而採用調和平均數形式來計算,使調和平均數的計算結果與加權算術平均數的計算結果相同,所以:
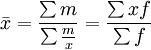
在實際應用加權算術平均數時,需註意權數的選擇。
應用平均指標必須註意的問題有:⑴計算和應用平均指標,必須註意現象總體的同質性;⑵用組平均數補充說明總平均數;⑶計算和運用平均數時,要註意極端數值的影響,因為算術平均數受極端數值的影響很明顯。
3、眾數和中位數
眾數和中位數是兩個位置平均數,在一定條件下用它們反映變數數列的一般水平是非常有效的。
眾數是總體中出現次數最多的變數值。在單位數不多或一個無明顯集中趨勢的資料中,眾數的測定沒有意義。一般來講,只有根據分組數列才能確定眾數。
中位數是將總體各單位標誌值按大小順序排列後,處於中間位置的那個數值。根據未分組資料和分組資料都可確定中位數。
1、把總體各單位標誌值的差異抽象化了。
2、平均指標是個代表值,代表總體各單位標誌值的一般水平。
平均指標的作用主要表現在:
1、它可以反映總體各單位變數分量分佈的集中趨勢,可以用來比較同類現象在不同單位發展的一般水平。
2、用來比較同一單位的同類指標在不同時期的發展狀況。
3、還可以用來分析現象之間的依存關係等相對指標數值的表現形式,有名數和無名數兩種。
平均指標與強度相對指標的區別
區別主要表現在以下兩點:
1、指標的含義不同。強度相對指標說明的是某一現象在另一現象中發展的強度、密度或普遍程度;而平均指標說明的是現象發展的一般水平。
2、計算方法不同。強度相對指標與平均指標,雖然都是兩個有聯繫的總量指標之比,但是,強度相對指標分子與分母的聯繫,只表現為一種經濟關係,而平均指標是在一個同質總體內標誌總量和單位總量的比例關係。分子與分母的聯繫是一種內在的聯繫,即分子是分母(總體單位)所具有的標誌,對比結果是對總體各單位某一標誌值的平均。








歸納的很好,挺有用的,贊一個!