平均指标
出自 MBA智库百科(https://wiki.mbalib.com/)
平均指标(Average Indicators)
目录 |
平均指标又称“统计平均数”,用以反映社会经济现象总体各单位某一数量标志在一定时间、地点条件下所达到的一般水平的综合指标。
平均指标的种类有:算术平均数、调和平均数、几何平均数、众数和中位数。前三种平均数是根据总体所有标志值计算的所以称为数值平均数,后两种平均数是根据标志值所处的位置确定的,因此称为位置平均数。
1、算术平均数的计算
算术平均数是计算平均指标的最常用方法,它的基本公式形式是总体标志总量除以总体单位总量。在实际工作中,由于资料的不同,算术平均数有两种计算形式:即简单算术平均数和加权算术平均数。
简单算术平均数:
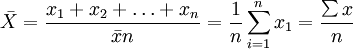
其中:---  算术平均数,X---各单位标志值(变量值),n---总体单位数(项数)。
算术平均数,X---各单位标志值(变量值),n---总体单位数(项数)。
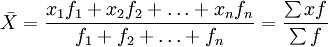
其中: ----代表算术平均数,x 代表各单位标志值(变量值),f 代表各组单位数(项数)。
----代表算术平均数,x 代表各单位标志值(变量值),f 代表各组单位数(项数)。
简单算术平均数适用于未分组的统计资料,如果已知各单位标志值和总体单位数,可采用简单算术平均数方法计算。
加权算术平均数适用于分组的统计资料,如果已知各组的变量值和变量值出现的次数,则可采用加权算术平均数计算。在“加权算术平均数=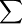 (各组变量值×各组次数)/
(各组变量值×各组次数)/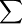 各组次数”,公式中,各组次数具有权衡各组变量值轻重的作用,某一组的次数越大,则该组的变量值对平均数的影响就越大,反之越小。加权算术平均数的大小受两个因素的影响,其一是受变量值大小的影响。其二是受次数分配值即各组次数占总次数比重的影响。加权算术平均数中的权数,指的就是标志值出现的次数或各组次数占总次数的比重。在计算平均数时,由于出现次数多的标志值对平均数的形成影响大些,出现次数少的标志值对平均数的形成影响小些,因此就把次数称为权数。在分组数列的条件下,当各组标志值出现的次数或各组次数所占比重均相等时,权数就失去了权衡轻重的作用,这时用加权算术平均数计算的结果与用简单算术平均数计算的结果相同。
各组次数”,公式中,各组次数具有权衡各组变量值轻重的作用,某一组的次数越大,则该组的变量值对平均数的影响就越大,反之越小。加权算术平均数的大小受两个因素的影响,其一是受变量值大小的影响。其二是受次数分配值即各组次数占总次数比重的影响。加权算术平均数中的权数,指的就是标志值出现的次数或各组次数占总次数的比重。在计算平均数时,由于出现次数多的标志值对平均数的形成影响大些,出现次数少的标志值对平均数的形成影响小些,因此就把次数称为权数。在分组数列的条件下,当各组标志值出现的次数或各组次数所占比重均相等时,权数就失去了权衡轻重的作用,这时用加权算术平均数计算的结果与用简单算术平均数计算的结果相同。
2、调和平均数的计算
在实际工作中,有时由于缺乏总体的单位数资料,而不能直接计算平均数,这时就可采用调和平均数计算。因此在统计工作中,调和平均数常常被作为算术平均数的变形来使用。调和平均数也有简单调和平均数和加权调和平均数两种形式。
例2、某月某企业按工人劳动生产率高低分组的生产班组数和产量资料如下:
| 按工人劳动生产率 分组(件/人) | 生产班组 | 产量(件) |
|---|---|---|
| 50-60 60-70 70-80 80-90 90以上 | 10 7 5 2 1 | 8250 6500 5250 2550 1520 |
试计算该企业工人平均劳动生产率。
解:列计算表如下:
| 按工人劳动生产率 分组(件/人) | 组中值 | 产量(件) | 人数 |
|---|---|---|---|
| 50-60 60-70 70-80 80-90 90以上 | 55 65 75 85 95 | 8250 6500 5250 2550 1520 | 150 100 70 30 16 |
| 合 计 | 24070 | 366 |
工人平均劳动生产率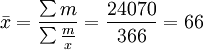 (件/人)
(件/人)
注意本题计算中权数的选择。资料中“生产班组”可以是次数,但并不是合适的权数。因为本题中的工人劳动生产率是按件/人计算的,和生产班组没有直接关系,所以它不能作为权数进行平均数的计算。本题应以“产量”权数,进行加权调和平均数的计算。
加权算术平均数与加权调和平均数是计算平均指标时常常用到的两个指标。加权算术平均数中的权数一般情况下是资料已经分组得出分配数列的情况下标志值的次数。而加权调和平均数的权数是直接给定的标志总量。在经济统计中,经常因为无法直接得到被平均标志值的相应次数的资料而采用调和平均数形式来计算,使调和平均数的计算结果与加权算术平均数的计算结果相同,所以:
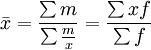
在实际应用加权算术平均数时,需注意权数的选择。
应用平均指标必须注意的问题有:⑴计算和应用平均指标,必须注意现象总体的同质性;⑵用组平均数补充说明总平均数;⑶计算和运用平均数时,要注意极端数值的影响,因为算术平均数受极端数值的影响很明显。
3、众数和中位数
众数和中位数是两个位置平均数,在一定条件下用它们反映变量数列的一般水平是非常有效的。
众数是总体中出现次数最多的变量值。在单位数不多或一个无明显集中趋势的资料中,众数的测定没有意义。一般来讲,只有根据分组数列才能确定众数。
中位数是将总体各单位标志值按大小顺序排列后,处于中间位置的那个数值。根据未分组资料和分组资料都可确定中位数。
1、把总体各单位标志值的差异抽象化了。
2、平均指标是个代表值,代表总体各单位标志值的一般水平。
平均指标的作用主要表现在:
1、它可以反映总体各单位变量分量分布的集中趋势,可以用来比较同类现象在不同单位发展的一般水平。
2、用来比较同一单位的同类指标在不同时期的发展状况。
3、还可以用来分析现象之间的依存关系等相对指标数值的表现形式,有名数和无名数两种。
平均指标与强度相对指标的区别
区别主要表现在以下两点:
1、指标的含义不同。强度相对指标说明的是某一现象在另一现象中发展的强度、密度或普遍程度;而平均指标说明的是现象发展的一般水平。
2、计算方法不同。强度相对指标与平均指标,虽然都是两个有联系的总量指标之比,但是,强度相对指标分子与分母的联系,只表现为一种经济关系,而平均指标是在一个同质总体内标志总量和单位总量的比例关系。分子与分母的联系是一种内在的联系,即分子是分母(总体单位)所具有的标志,对比结果是对总体各单位某一标志值的平均。








归纳的很好,挺有用的,赞一个!