等額還款抵押貸款
出自 MBA智库百科(https://wiki.mbalib.com/)
等額還款抵押貸款(Constant payment mortgage,CPM)
目錄 |
什麼是等額還款抵押貸款[1]
等額還款抵押貸款也稱完全均付抵押貸款,是在整個貸款期內以固定利率按月均等額償還貸款本息的貸款方式。
等額還款抵押貸款的利率[2]
在等額還款抵押貸款下,貸款利率在整個抵押貸款合同期內不隨市場利率變化而改變,一旦未來市場實際利率上升,貸款機構的負債成本將增加,而資產的收益水平卻保持不變,於是金融機構承擔了全部的利率風險。所以,等額還款抵押貸款的利率一般高於可調利率抵押貸款的初期利率,併在貸款合同期內保持較高的利率水平,是為了沖抵利率變化帶來的風險。
等額還款抵押貸款的計算[3]
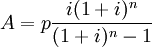
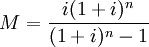
②貸款餘額的計算。貸款餘額是指當分期付款的貸款在經過一定償還期以後尚未清償的貸款本金數額。在發達國家,居民一生中往往要遷徙幾次,這就涉及出售舊房購買新房,也就要歸還舊貸款,申請新貸款。如加拿大居民平均5~7年就要遷居一次,美國住房抵押貸款實際平均還款年限通常在8~12年。因此,對貸款機構和借款人來說都需要計算貸款餘額。在抵押貸款現金流分析等工作中也需要計算貸款餘額。
貸款餘額可以用年金現值的方法計算。償還一定時期後,貸款餘額實際上就是計算時點的年金現值。設貸款餘額為p1,已歸還期數為n1,根據年金現值的計算公式,該時點的貸款餘額為: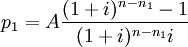
③每月本息償還額中本金和利息的計算。由上述貸款餘額的計算方法,可以得出,還款期內某月本息償還額中的本金部分就是該月相鄰兩期貸款餘額之差。如果計算第N期月償還額的本金PN,計算公式為:
第N期月償還額的本金PN=第N-1期貸款餘額—第N期貸款餘額
計算出本金以後,第N期償還額的利息IN=月本息償還額A—第N期月償還額的本金PN。
另一種簡單的計算方法如下。
第N期償還額的利息IN=第N-1期貸款餘額×貸款月利率
第N期月償還額的本金PN=月本息償還額—第N期償還額的利息IN
等額還款抵押貸款還款分析[3]
①月本息償還額中本金和利息的關係。根據以上計算公式,計算還款中貸款餘額、本金、利息的變化情況如下:
由於月還本付息的金額是固定不變的,剩餘本金隨著時間的推移而下降,每月本息償還額中利息部分的比重逐步下降,而本金部分的比率逐步上升,直到貸款本息全部清償為止。
等額還款抵押貸款在貸款初期每月還款額大部分用於歸還貸款利息,隨著時間的推移,每月還款額中本金逐漸增加。
②月本息償還額與貸款期限、貸款利率的關係。月本息償還額受借款人家庭收入和支出水平的共同制約。在抵押貸款中,貸款機構和借款人都十分關心月本息償還額的大小,因為它直接關係到借款人的支付能力和貸款的保證程度。從計算公式中可以看出,月本息償還額與貸款總額、貸款期限、貸款利率有著密切關係。在其他變數不變的情況下,月本息償還額與貸款總額成正向相關關係;並隨著貸款利率的上升而提高。延長貸款期限,月本息償還額隨之下降,最終趨於貸款總額與月利率的乘積(這可以從月本息償還額計算公式中計算出來,當時間n趨於無窮大時,A=pi)。這說明瞭貸款期限增加到一定年限以後,延長貸款年限對月本息償還額影響不大,對減輕借款人的還款壓力作用十分有限。
1.每月還款額固定不變
2.在還款初期還款額大部分用於歸還貸款利息,隨著時間的推移,每月還款額中本金逐漸增加
3.每期還款中利息所占的比重逐漸下降
4.每期還款中本金所占比重逐漸上升
等額還款抵押貸款的利率風險控制[1]
利率風險是未來利率變動的不確定性所產生的金融資產價值變動的可能性。在固定利率抵押貸款下,利率在整個合同期內不隨市場利率變化而改變,金融機構承擔了全部的利率風險。一旦未來市場實際利率上升,貸款機構的負債成本將增加,在資產的收益水平不變的背景下,貸款機構的贏利水平就必然會降低。
常用的控制利率風險的方法是由借貸雙方平分風險,因此,等額還款抵押貸款利率一般高於可調利率抵押貸款初期的利率,以便由較高利率的收益來沖抵利率變化帶來的利率風險。如在美國,20世紀30年代至70年代,利率保持基本穩定,波動幅度不大,銀行大多以固定利率抵押貸款為主要貸款方式;70年代末期,因市場利率波動的加劇,可調利率的抵押貸款發展迅速;到80年代後期,市場利率趨於平穩,固定利率抵押貸款又成為市場主流品種。







