理論責任準備金

出自 MBA智库百科(https://wiki.mbalib.com/)

　　理論責任準備金，是指按照生命表和預定利率，結合險種特點和繳費方式等等精算因素，將當年收取的純保險費扣除當年應該攤付的給付成本之後，按照壽險原理應該提留的責任準備金數額。^[1]

　　按照估計準備金的時間不同，理論責任準備金可分為期初、期中和期末準備金。期初準備金是保險年度初的準備金，它等於上年末準備金加上本年純均衡保險費；期末準備金就是前面介紹的用追溯法和預期法計算的準備金，又稱年末準備金；期中準備金是期初準備金和期末準備金的算術平均數。期初準備金主要用於確定分紅保險單的紅利。期中準備金主要為人壽保險公司的年報使用。因為人壽保險單是在1年內不同時間簽發的，公司的年報於12月31日編製，此時要計算每份保險單的期末準備金是非常困難的。為了編製公司年報起見，假定一個年度內簽發的保險單是平均分佈的，期中準備金在公司年報上用來表示的準備金負債。期末準備金可以用於紅利分配，也可以用於研究不可沒收的現金價值、再保險的方式。

　　理論責任準備金的計算有過去法和未來法。

　　1．過去法

　　過去法以分析已繳的純保險費為出發點。假定生命表內所列年齡為x歲的人，全部向保險公司投保同一保險條件、同一保險期限、同一繳費次數的人壽保險，保險金額均為l元，則在投保後第t年末，被保險人的年齡為x+t歲時，已繳純保險費的積存值，減去被保險人的年齡x+t歲時，根據生命表保險公司已支付保險金的積存值。由於這種計算方式涉及生存分紅年金和期末死亡保險費，故在此僅給出相應的計算公式(用_tV_x表示在第t年的準備金)。

　　如果繳費次數和保險年限相同，則：

　　_tV_x=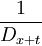[_nP_x:n(N_x − N_{x + t}) − (M_x − M_{x + t})]

　　如果保險期限為n年，保險費在最初m年交付，t≤m，則：

　　_tV_x=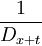[_mP_x:n(N_x − N_{x + t}) − (M_x − M_{x + t})]

　　如果保險期限為n年，保險費在最初m年交付，t>m，則：

　　_tV_x=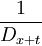[_mP_x:n(N_x − N_{x + m}) − (M_x − M_{x + t})]

　　如果是純粹生存保險，由於保險公司在以往t年內並未有任何給付，以上公式中含有M_x的項均不出現。

　　假定某人現年x歲，投保n年定期死亡保險，保險金額為l元，保險費一次躉繳，不難求出在t年年末應提存的準備金為

　　_tV_x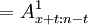

　　這說明，第t年年末應提存的準備金，正好是x+t歲的人投保n-t年期定期死亡保險的躉繳純保險費。由此可見責任準備金的意義。

　　2．未來法

　　未來法是與過去法相對的一種方法，其以分析未繳的純保險費為出發點。按照這一方法，被保險人x+t歲時，_tV_x的值等於未來保險責任的現值減去待收保險費的現值(A)減去待收保險費的現值(B)。A等於被保險人自x+t歲開始投保的保險責任，即自x+t歲起至到期日為止的躉繳純保險費。B形成一種前付生存年金，以原保險單上待收的年度純保險費作為每年的固定收入額。根據這種分析，以定期死亡保險為例，責任準備金的計算公式如下。

　　如果繳費次數與保險年限相同，則：

　　_tV_x=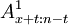 - _nP_n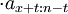

　　如果保險期限為n年，保險費在最初m年交付，t≤m，則因在計算準備金時，尚有(m-t)次年度保險費待收，所以：

　　_tV_x=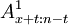 - _mP_n

　　如果保險期限為n年，保險費在最初m年交付，t>m，則在計算準備金時，已無待收的保險費，所以：

　　_tV_x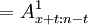

　　在上述3個公式中，如果將x+n推至極限年齡ω，則可得到終身死亡保險的準備金計算公式；如果將第一項分別改為_n-tE_x+t或A_{x + t:n − t}，則分別得到生存保險或混合保險的責任準備金的計算公式。

　　需要說明的是，理論責任準備金僅與保險條件、保險期限、繳費方式及保險金額等有關，而與計算方法無關。因為，根據計算純保險費的基本原理公式(所有純保險費在保單簽發日的現值一根據生命表所有保險責任在保單簽發日的現值)，經過t年後，有以下關係。

　　t年以前全部已收純保險費的積存值+t年以後全部未收純保險費的現值=根據生命表t年以前已付保險金的積存值+t年以後保險責任的現值

　　將上面的等式移項有：t年以前全部已收保險費的積存值-根據生命表t年以前已付保險金的積存值=t年以後保險責任的現值-t年以後全部未收純保險費的現值

　　以上公式左端所得結果即為按過去法所得的_tV_x，右端所得結果即為按未來法所得的_tV_x。一般按未來法計算比較方便。

• 實際責任準備金