理论责任准备金

出自 MBA智库百科(https://wiki.mbalib.com/)

　　理论责任准备金，是指按照生命表和预定利率，结合险种特点和缴费方式等等精算因素，将当年收取的纯保险费扣除当年应该摊付的给付成本之后，按照寿险原理应该提留的责任准备金数额。^[1]

　　按照估计准备金的时间不同，理论责任准备金可分为期初、期中和期末准备金。期初准备金是保险年度初的准备金，它等于上年末准备金加上本年纯均衡保险费；期末准备金就是前面介绍的用追溯法和预期法计算的准备金，又称年末准备金；期中准备金是期初准备金和期末准备金的算术平均数。期初准备金主要用于确定分红保险单的红利。期中准备金主要为人寿保险公司的年报使用。因为人寿保险单是在1年内不同时间签发的，公司的年报于12月31日编制，此时要计算每份保险单的期末准备金是非常困难的。为了编制公司年报起见，假定一个年度内签发的保险单是平均分布的，期中准备金在公司年报上用来表示的准备金负债。期末准备金可以用于红利分配，也可以用于研究不可没收的现金价值、再保险的方式。

　　理论责任准备金的计算有过去法和未来法。

　　1．过去法

　　过去法以分析已缴的纯保险费为出发点。假定生命表内所列年龄为x岁的人，全部向保险公司投保同一保险条件、同一保险期限、同一缴费次数的人寿保险，保险金额均为l元，则在投保后第t年末，被保险人的年龄为x+t岁时，已缴纯保险费的积存值，减去被保险人的年龄x+t岁时，根据生命表保险公司已支付保险金的积存值。由于这种计算方式涉及生存分红年金和期末死亡保险费，故在此仅给出相应的计算公式(用_tV_x表示在第t年的准备金)。

　　如果缴费次数和保险年限相同，则：

　　_tV_x=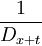[_nP_x:n(N_x − N_{x + t}) − (M_x − M_{x + t})]

　　如果保险期限为n年，保险费在最初m年交付，t≤m，则：

　　_tV_x=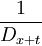[_mP_x:n(N_x − N_{x + t}) − (M_x − M_{x + t})]

　　如果保险期限为n年，保险费在最初m年交付，t>m，则：

　　_tV_x=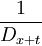[_mP_x:n(N_x − N_{x + m}) − (M_x − M_{x + t})]

　　如果是纯粹生存保险，由于保险公司在以往t年内并未有任何给付，以上公式中含有M_x的项均不出现。

　　假定某人现年x岁，投保n年定期死亡保险，保险金额为l元，保险费一次趸缴，不难求出在t年年末应提存的准备金为

　　_tV_x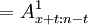

　　这说明，第t年年末应提存的准备金，正好是x+t岁的人投保n-t年期定期死亡保险的趸缴纯保险费。由此可见责任准备金的意义。

　　2．未来法

　　未来法是与过去法相对的一种方法，其以分析未缴的纯保险费为出发点。按照这一方法，被保险人x+t岁时，_tV_x的值等于未来保险责任的现值减去待收保险费的现值(A)减去待收保险费的现值(B)。A等于被保险人自x+t岁开始投保的保险责任，即自x+t岁起至到期日为止的趸缴纯保险费。B形成一种前付生存年金，以原保险单上待收的年度纯保险费作为每年的固定收入额。根据这种分析，以定期死亡保险为例，责任准备金的计算公式如下。

　　如果缴费次数与保险年限相同，则：

　　_tV_x=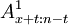 - _nP_n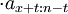

　　如果保险期限为n年，保险费在最初m年交付，t≤m，则因在计算准备金时，尚有(m-t)次年度保险费待收，所以：

　　_tV_x=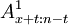 - _mP_n

　　如果保险期限为n年，保险费在最初m年交付，t>m，则在计算准备金时，已无待收的保险费，所以：

　　_tV_x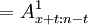

　　在上述3个公式中，如果将x+n推至极限年龄ω，则可得到终身死亡保险的准备金计算公式；如果将第一项分别改为_n-tE_x+t或A_{x + t:n − t}，则分别得到生存保险或混合保险的责任准备金的计算公式。

　　需要说明的是，理论责任准备金仅与保险条件、保险期限、缴费方式及保险金额等有关，而与计算方法无关。因为，根据计算纯保险费的基本原理公式(所有纯保险费在保单签发日的现值一根据生命表所有保险责任在保单签发日的现值)，经过t年后，有以下关系。

　　t年以前全部已收纯保险费的积存值+t年以后全部未收纯保险费的现值=根据生命表t年以前已付保险金的积存值+t年以后保险责任的现值

　　将上面的等式移项有：t年以前全部已收保险费的积存值-根据生命表t年以前已付保险金的积存值=t年以后保险责任的现值-t年以后全部未收纯保险费的现值

　　以上公式左端所得结果即为按过去法所得的_tV_x，右端所得结果即为按未来法所得的_tV_x。一般按未来法计算比较方便。

• 实际责任准备金