模糊決策

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

什麼是模糊決策

　　模糊決策是指在模糊環境下進行決策的數學理論和方法。嚴格地說，現實的決策大多是模糊決策。模糊決策的研究開始較晚，但涉及的面很廣，還沒有明確的範圍。常用的模糊決策方法有模糊排序、模糊尋優和模糊對策等。這類問題一般具有大系統特征，系統之間的關係十分複雜；存在不能準確賦值的變數，這些變數屬於模糊因素；涉及到一定的主觀因素，使得子系統之間、變數之間的關係不清晰，從而必須藉助排序、模糊評判等方法來進行處理。

[編輯]

常用模糊決策的方法^[1]

　　常用的模糊決策方法有模糊排序、模糊尋優和模糊對策等。

　　模糊排序

　　研究決策者在模糊環境下如何確定各種決策方案之間的優劣次序。例如，給定一個模糊序（一個反身、傳遞的二元模糊關係），或給定一個不傳遞的普通二元關係，如何近似地排出一個全序；對於有多種指標、多個效用函數的問題，如何利用模糊集合論的方法綜合成一個排優次序，多層次的決策問題又應當如何排序。這些問題都已獲得初步的解答。

　　模糊尋優

　　給定方案集及各種目標函數和限制條件以後，尋求最優方案便成了一個優化問題。若目標函數或約束條件是模糊的，這時的最優化就稱為模糊尋優。目標函數模糊化的一種途徑是以模糊數作為目標函數值，通過模糊數的分析、運算來尋求條件極值。約束條件的模糊化是將約束定義成模糊集合。在線性規劃中這樣的推廣導致模糊線性規劃的研究，其結果是使普通的線性規劃應用範圍更廣，能更加靈活地適應各種不同的情況。在非線性規劃中有非對稱模型和對稱模型兩種數學模型。

　　①非對稱模型：把接受約束作為先決條件，目標與約束二者的地位不是對稱的。給定論域X上的目標函數f(x)和X上的約束條件模糊集合 D，所謂在約束D之下極大化f的最優解M，就是X上的一個模糊子集,它具有隸屬函數當等式右端的集合為空集時，uM(x)等於0。

　　 $u_m(x)\cong sup{\lambda|\lambda\subset[0,1],f(x)=max_{u:u_{M}(u)\ge \lambda}f(u)}$

　　 ②對稱模型：把目標和約束兩者置於對稱的地位。給定論域X上的目標函數f(x)和模糊限制集合D。設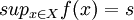 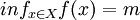$sup_{x\in X}f(x)=s$ , $inf_{x\in X}f(x)=m$ .令 $u F (x) = (f (x) - m) / (s - m)$ F是X上的一個模糊子集，其隸屬函數與目標函數呈線性關係，稱為目標集合，記為 $u N (x) = m i n (F (x), D (x))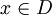$ .( $x\in D$ ),N 就是對稱模型下的模糊最優解。