模糊線性規劃
出自 MBA智库百科(https://wiki.mbalib.com/)
模糊線性規劃(fuzzy linear programming)
目錄 |
模糊線性規劃模型及解法[1]
模糊線性規劃(fuzzy linear programming)是經典線性規劃的一種推廣,它是將線性約束的邊界模糊化,從而使人們能在較寬鬆的條件下求得優化的條件與優化的極值
一般地,普通線性規劃的模型如下:
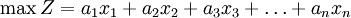 。
。
 (1)。
(1)。
約束條件中的(*)表示(≥)、(≤)或(=)。
顯然,從上述模型可以看出,普通線性規劃的目標函數繫數清晰、約束條件中的關係確定,這對於解決一些目標明確、關係確定的問題是很有效的,但當面對繫數模糊、非確定性關係的問題時,它顯得就無能為力了。因此,為瞭解決實際生活中經常遇到的具有模糊性的問題時,人們提出了模糊線性規劃。它自誕生起,就受到了廣泛的關註,經過二十幾年的發展,已經基本趨於成熟,併在實際問題中得到了大量的應用,效果甚佳。
模糊線性規劃一般可劃分為清晰繫數型、模糊繫數型和非精確繫數型等,實質上它們都是在普通線性規劃的基礎上,將其約束條件和目標函數進行模糊化得到的,一般來說,其可採用如下的模型進行表示:
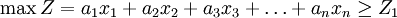 。
。
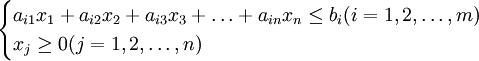 (2)
(2)
utf − 8 其中: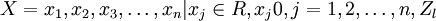 為式(2)對應的普通線性規劃的最優解,設對於第i個約束條件,有X中的一個模糊子集Di與之對應,“ ”表示“大約大於等於”,“ ”表示“大約小於等於”。令i個約束條件的伸縮值為di,當第i個約束條件完全滿足時,其隸屬度為1,當第i個約束條件超過bi + di時,其隸屬函數度為0,其他情況下,其隸屬函數的值介於0和1之間,設其隸屬函數為線性函數,則其形式如下:
為式(2)對應的普通線性規劃的最優解,設對於第i個約束條件,有X中的一個模糊子集Di與之對應,“ ”表示“大約大於等於”,“ ”表示“大約小於等於”。令i個約束條件的伸縮值為di,當第i個約束條件完全滿足時,其隸屬度為1,當第i個約束條件超過bi + di時,其隸屬函數度為0,其他情況下,其隸屬函數的值介於0和1之間,設其隸屬函數為線性函數,則其形式如下:
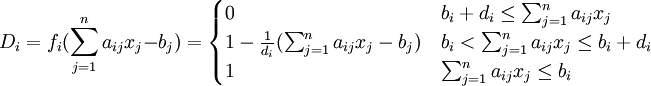 (3)
(3)
設目標函數對應於X中的一個模糊子集M∈F(x),且令目標函數的伸縮值為d0,其中d0是在約束條件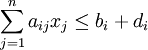 (i=1,2,…,m)下對應的普通線性規劃的最優解與Zl之差,從式(2)可以看出,目標函數最優解應大於Zl,因此當目標函數值小於Zl時,目標函數的隸屬度為0,當目標函數的值大於Zl+d0時,目標函數的隸屬度為1,其他情況下,隸屬函數的值介於0和1之間,同樣令隸屬函數在0和1之間呈線性變化,則目標函數的隸屬函數形式如下:
(i=1,2,…,m)下對應的普通線性規劃的最優解與Zl之差,從式(2)可以看出,目標函數最優解應大於Zl,因此當目標函數值小於Zl時,目標函數的隸屬度為0,當目標函數的值大於Zl+d0時,目標函數的隸屬度為1,其他情況下,隸屬函數的值介於0和1之間,同樣令隸屬函數在0和1之間呈線性變化,則目標函數的隸屬函數形式如下:
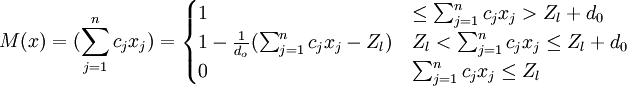 (4)
(4)
令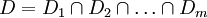 為對應約束條件AX≤B的模糊約束集。設模糊優越解集為S,則S=
為對應約束條件AX≤B的模糊約束集。設模糊優越解集為S,則S=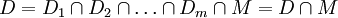 ,為了兼顧模糊約束集D和模糊目標集M,可採用模糊前判決,從而找到最佳點x * ,使
,為了兼顧模糊約束集D和模糊目標集M,可採用模糊前判決,從而找到最佳點x * ,使
即由M誘導可能性測度∏,D對該測度的可能度∏(D)=D·M,從而最佳點x * 滿足。
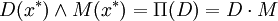
由於
所以模糊線性規劃問題可歸結為求普通線性規劃的問題為
maxλ
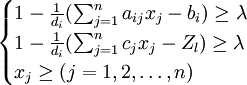 (5)
(5)
對模型(5)求解,其最優解即為模型(2)的模糊最優解[2]
在上述求解過程中,約束條件中的伸縮量d_i是根據所解決問題的實際情況,通過綜合分析和比較後確定的,此外,本文還假定了介於0和1之間的約束條件與目標函數的隸屬函數呈線性變化,這一近似假定簡化了計算,但對結果的影響不會超過實際情況所允許的範圍,因而假定是可取的。
案例一:模糊線性規劃在企業生產管理中的應用[1]
一、應用步驟
同線性規劃一樣,建立模糊數學規劃模型分四個步驟[3]:
第一,確定決策變數,根據實際問題的情況,把決策系統中的可控因素作為決策變數,通常用帶有不同下標的英文字母表示,例如用: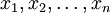 表示年終計劃中不同種產品的產量。線性規劃的量應為正值,因為在實際問題中變數所代表的均為實物,不能為負。
表示年終計劃中不同種產品的產量。線性規劃的量應為正值,因為在實際問題中變數所代表的均為實物,不能為負。
第二,確定目標函數。用形式表示出來的實際系統的期望目標稱為目標函數。線性規劃的目標函數基本上是求系統目標的極值,如:利潤極大、效率極大等極大值或成本極小、費用極小等極小值。
模糊線性規劃的目標在一定的範圍內具有相對的伸縮性。
第三,確定約束條件。約束條件是指實現系統目標的限制因素,通常包括生產力約束,原材料、能源約束,庫存水平約束等。對於模糊線性規劃來說,約束條件一般是模糊的,具有一定的彈性。
二、模糊線性規劃在生產管理中的應用
現以某飼料廠為例,設其只有一條生產線,能生產三種飼料A、B和C,飼料A每噸利潤為3萬元,飼料B每噸利潤5萬元,飼料C每噸利潤4萬元。產品A每噸耗費Ⅰ類原料2噸,產品B每噸需耗費Ⅰ類原料3噸和Ⅱ類原料2噸,飼料C每噸需耗費Ⅱ類原料5噸。該廠現有庫存Ⅰ類原料8噸多,Ⅱ類原料10噸多,生產料飼料A噸需3 h的生產時間、生產飼料B每噸需2 h的生產時間、生產飼料C每噸需4 h的生產時間,每天的總生產時間為16h,工廠允許少量加班。問怎樣安排鑒別類飼料的生產數量才能保證工廠能夠獲得最大的經濟效益。
(1)選取決策變數
設x1=每天生產的A類飼料數
x2=每天生產的B類飼料數
x3=每天生產的C類飼料數
(2)確定目標函數
根據題意,工廠的最終目標是合理分配三種飼料的生產比例,從而獲得較高的利潤,所以可以建立目標函數為:。
Z = 3x1 + 5x2 + 4x3
(3)確定約束條件顯然,可以把庫存的原料總量和飼料的生產時間作為約束,那麼有:
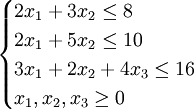
通過上述分析,可得其線性規劃的模型如下
maxZ = 3x1 + 5x2 + 4x3
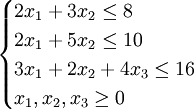 (6)
(6)
利用單純形法求之得
[x1,x2,x3] = [104 / 41,40 / 41,66 / 41],Zl = 776 / 41
顯然在上述問題中,約束條件是具有伸縮性的,比如庫存原料量和生產時間,因此這是一個模糊線性規劃問題,與模型(2)相對應的模糊線性規劃的模型為:
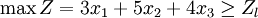
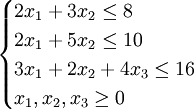 (7)
(7)
取模型(6)中的條件1,2,3的伸縮量為1.3,1,1,此時對應該條件的線性規劃的最優解為[x1,x2,x3] = [2.059,1.5609,2.254],Zl = 19.34
這樣,由於約束條件的伸縮值為d1 = 1.3,d2 = 1,d3 = 1,目標函數的伸縮值為d0 = 19.34 − 18.927 = 0.413,模糊線性規劃模型(7)可變為普通線性規劃模型為:
maxλ
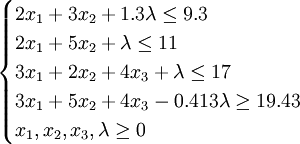 (8)
(8)
對上述模型求解,可得對應於最大隸屬度λ = 0.312下,其最大利潤為19.14,顯然比普通線性規劃的利潤多0.213萬元。
(1)在企業的生產過程中,存在著許多不確定的因素,這些因素導致企業的管理和決策具有一定的彈性,這也給企業的管理者帶來了比較麻煩的問題,而模糊線性規劃是解決這類難題的行之有效的方法。
(2)模糊線性規劃利用“令人滿意的解”代替了普通線性規劃的“最優的解”,更符合實際,但伸縮值的選擇有時要參考實際情況,有時又要藉助以往的實踐經驗,有一定的難度,應該慎之又慎,要具體問題具體分析。
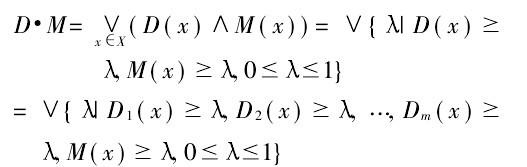








謝謝