模糊集合

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

模糊集合(Fuzzy Sets)

什麼是模糊集合

　　模糊集合是由在某種程度上屬於它的原素構成的。從隸屬到不隸屬的轉變，不像普通集合那樣是硬性的，而是軟性的。同樣，模糊邏輯的對象是不明確的真理，模糊聯結詞和推論規則與古典的二值邏輯是對立的。

　　給定一個論域 U ，那麼從 U 到單位區間 [0,1] 的一個映射

　　 $\mu_{A}: U \mapsto [0,1]$

　　稱為 U 上的一個模糊集合，或 U 的一個模糊子集，

　　要註意，嚴格地說，模糊集合或子集是映射所確定的序對集，但由於模糊子集完全由其隸屬函數所確定，因而我們不區分映射和映射所確定的序對集，而總是直接把模糊子集定義為一個滿足上述定義的映射。

　　模糊集合可以記為 A 。

　　映射（函數） μ_A(·) 或簡記為 A(·) 叫做模糊集合 A 的隸屬函數。

　　對於每個 x ∈ U ， μ_A(x) 叫做元素 x 對模糊集合 A 的隸屬度。

　　模糊集合的常用表示法有下述幾種：

　　解析法，也即給出隸屬函數的具體表達式。

　　Zadeh 記法，例如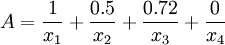 $A={1\over x_1}+{0.5\over x_2}+{0.72\over x_3}+{0\over x_4}$ 。分母是論域中的元素，分子是該元素對應的隸屬度。有時候，若隸屬度為0，該項可以忽略不寫。

　　序偶法，例如 $A = {(x 1,1),(x 2,0.5),(x 3,0.72),(x 4,0)}$ ，序偶對的前者是論域中的元素，後者是該元素對應的隸屬度。

　　向量法，在有限論域的場合，給論域中元素規定一個表達的順序，那麼可以將上述序偶法簡寫為隸屬度的向量式，如 A = (1,0.5,0.72,0) 。

[編輯]

模糊集合的運算

[編輯]

各種運算元

　　Zadeh 運算元，max 即為並，min 即為交

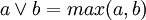
　　 $a\vee b=max(a,b)$

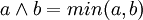
　　 $a\wedge b=min(a,b)$

　　代數運算元（概率和、代數積）

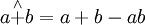
　　 $a\stackrel{\wedge}{+} b =a+b-ab$

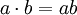
　　 $a\cdot b = ab$

　　有界運算元

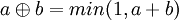
　　 $a\oplus b =min(1,a+b)$

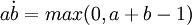
　　 $a\dot b = max(0,a+b-1)$

　　Einstein 運算元

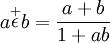
　　 $a\stackrel{+}{\epsilon} b = \frac{a+b}{1+ab}$

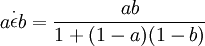
　　 $a\stackrel{\cdot}{\epsilon} b = \frac{ab}{1+(1-a)(1-b)}$

　　Hamacher 運算元，其中ν ∈ [0,+∞) 是參數，等於1時轉化為代數運算元，等於2時轉化為 Einstein 運算元

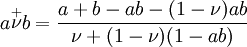
　　 $a\stackrel{+}{\nu} b = \frac{a+b-ab-(1-\nu)ab}{\nu+(1-\nu)(1-ab)}$

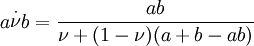
　　 $a\stackrel{\cdot}{\nu} b = \frac{ab}{\nu+(1-\nu)(a+b-ab)}$

　　Yager 運算元，其中 p 是參數，等於1時轉化為有界運算元，趨於無窮時轉化為 Zadeh 運算元

　　 $a Y p b = m i n 1,(a p + b p) 1 / p$

　　 $a y p b = 1 - m i n 1,[(1 - a) p + (1 - b) p] 1 / p$

　　λ-γ 運算元，其中 λ,γ∈ [0,1] 是參數

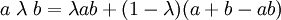
　　 $a\;\lambda\;b = \lambda ab+(1-\lambda)(a+b-ab)$

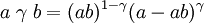
　　 $a\;\gamma\;b = (ab)^{1-\gamma}(a-ab)^\gamma$

　　Dobois-Prade 運算元，其中 λ ∈ [0,1] 是參數

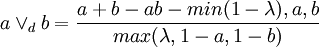
　　 $a\vee_d b = \frac{a+b-ab-min{(1-\lambda),a,b}}{max(\lambda,1-a,1-b)}$

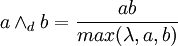
　　 $a\wedge_d b = \frac{ab}{max(\lambda,a,b)}$

[編輯]

運算元的性質

　　主要運算元的性質對比表如下（.表示不滿足，-表示未驗證）：

運算元	結合律	交換律	分配律	互補律	同一律	冪等律	支配律	吸收律	雙重否定律	德·摩根律
Zedah	√	√	√	.	√	√	√	√	√	√
代數	√	√	.	.	√	.	√	.	-	√
有界	√	√	.	√	√	.	√	√	-	√

　　線性補償是指：

$(\forall x,y,k \in [0,1])(x+k \wedge y-k\ \Rightarrow\ U(x+k,y-k)=U(x,y))$ ^[1]

運算元的並運算	冪等律	排中律	分配律	結合律	線性補償
Zadeh	√	.	√	√	.
代數	.	.	.	√	.
有界	.	√	.	.	√
Hamacher r = 0	.	.	.	√	.
Yager	.	.	.	√	.
Hamacher	.	.	.	√	.
Dobois-Prade	.	.	.	√	.

[編輯]

模糊集合之間的距離

[編輯]

使用度量理論

　　可以使用一般的度量理論來描述模糊集合之間的距離。在這個意義上，我們需要在模糊冪集 F(U) 上建立一個度量，此外，我們還可能需要將此度量標準化，也即映射到 [0,1] 區間上。例如可以這樣來標準化 Minkowski 距離：

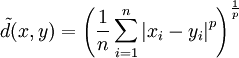
　　 $\tilde{d}(x,y)=\left({1\over n}\sum\limits_{i=1}^n \left| x_i - y_i \right|^p \right)^{1\over p}$

[編輯]

貼近度

　　另一種是使用貼近度概念。在某種意義上，貼近度就是 1 - 距離（這裡的距離是上述標準化意義上的距離）。而之所以應用這個變換，是考慮到“度”的概念的直覺反映——距離越近，貼近的程度顯然越“高”，因此它恰為距離的反數。

　　除了距離外，還有一些與模糊集合的特殊操作有關係的貼近度定義。

　　最大最小貼近度

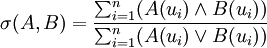
　　 $\displaystyle \sigma(A,B)=\frac{\sum_{i=1}^{n}(A(u_i)\wedge B(u_i))}{\sum_{i=1}^{n}(A(u_i)\vee B(u_i))}$

　　算術平均最小貼近度

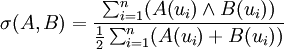
　　 $\displaystyle \sigma(A,B)=\frac{\sum_{i=1}^{n}(A(u_i)\wedge B(u_i))}{{1\over 2}\sum_{i=1}^{n}(A(u_i)+B(u_i))}$

　　幾何平均最小貼近度

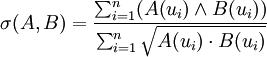
　　 $\displaystyle \sigma(A,B)=\frac{\sum_{i=1}^{n}(A(u_i)\wedge B(u_i))}{\sum_{i=1}^{n}\sqrt{A(u_i)\cdot B(u_i)}}$

　　指數貼近度

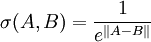
　　 $\displaystyle \sigma(A,B)=\frac{1}{e^{\|A-B\|}}$

　　模糊集合的模糊度

　　一個模糊集合 A 的模糊度衡量、反映了 A 的模糊程度，一個直觀的定義是這樣的：

　　設映射 D : F(U) → [0,1] 滿足下述5條性質：

　　清晰性：D(A) = 0 當且僅當 A ∈ P(U)。（經典集的模糊度恆為0。）

　　模糊性：D(A) = 1 當且僅當 ∀ u ∈ U 有 A(u) = 0.5。（隸屬度都為0.5的模糊集合最模糊。）

　　單調性：∀ u ∈ U，若 A(u) ≤ B(u) ≤ 0.5，或者 A(u) ≥ B(u) ≥ 0.5，則 D(A) ≤ D(B)。

　　對稱性：∀ A ∈ F(U)，有 D(A^c) = D(A)。（補集的模糊度相等。）

　　可加性：D(A∪B) + D(A∩B)=D(A) + D(B)。

　　則稱 D 是定義在 F(U) 上的模糊度函數，而 D(A) 為模糊集合 A 的模糊度。

　　可以證明符合上述定義的模糊度是存在的^[2]，一個常用的公式（分別針對有限和無限論域）就是

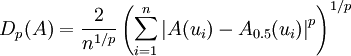
　　 $D_p(A)=\frac{2}{n^{1/p}}\left(\sum\limits_{i=1}^n\left|A(u_i)-A_{0.5}(u_i)\right|^p\right)^{1/p}$

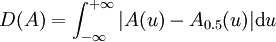
　　 $D(A)=\int_{-\infty}^{+\infty}|A(u)-A_{0.5}(u)|\mbox{d}u$

　　其中 p > 0 是參數，稱為 Minkowski 模糊度。特別地，當 p = 1 的時候稱為 Hamming 模糊度或 Kaufmann 模糊指標，當 p = 2 的時候稱為 Euclid 模糊度。

[編輯]

參考文獻

↑ Etienne E.Kerre等，模糊集合理論與近似推理[C]，武漢大學出版社，2004年，第103頁。
↑ 陳水利等，模糊集合理論及其應用[C]，科學出版社，2005年，第20頁。

取自"https://wiki.mbalib.com/zh-tw/%E6%A8%A1%E7%B3%8A%E9%9B%86%E5%90%88"

打开MBA智库App, 阅读完整内容打开App

如果您認為本條目還有待完善，需要補充新內容或修改錯誤內容，請編輯條目或投訴舉報。

本条目由以下用户参与贡献

Tracy.

頁面分類: 應用數學

評論(共0條)

提示:評論內容為網友針對條目"模糊集合"展開的討論，與本站觀點立場無關。

發表評論請文明上網，理性發言並遵守有關規定。

查看

工具▼

模糊集合

出自 MBA智库百科(https://wiki.mbalib.com/)

目錄

什麼是模糊集合

模糊集合的運算

各種運算元

運算元的性質

模糊集合之間的距離

使用度量理論

貼近度

參考文獻

温馨提示

本条目相关课程

本条目由以下用户参与贡献

評論(共0條)

導航

意见反馈

查看

工具▼

模糊集合

出自 MBA智库百科(https://wiki.mbalib.com/)

目錄

什麼是模糊集合

模糊集合的運算

各種運算元

運算元的性質

模糊集合之間的距離

使用度量理論

貼近度

參考文獻

温馨提示

本條目相關文檔

本条目相关课程

本条目由以下用户参与贡献

評論(共0條)

導航

意见反馈